Параграф 1. Изолированные особые точки однозначных аналитических функций.
Квант. 08.01.01. Определение изолированной особой точки однозначной аналитической функции (О)
Рассмотрим однозначную функцию  и точку
и точку  в которой функция не является аналитической
в которой функция не является аналитической
Пусть  аналитична в некоторой проколотой окрестности точки
аналитична в некоторой проколотой окрестности точки 
 (в самой точке
(в самой точке  функция может быть и не определена).
функция может быть и не определена).
Тогда точка  называется изолированной особой точкой однозначной аналитической функции
называется изолированной особой точкой однозначной аналитической функции 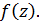
Квант. 08.01.02. Классификация изолированных особых точек однозначной аналитической функции (О)
Рассмотрим изолированную особую точку  однозначной аналитичекой функции
однозначной аналитичекой функции 
В проколотой окрестности точки 
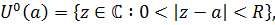
в которой функция 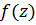 аналитична, разложим ее в ряд Лорана
аналитична, разложим ее в ряд Лорана
 Тогда
Тогда
1) Если главная часть в разложении Лорана отсутствует, т.е.

то точка  называется устранимой особой точкой.
называется устранимой особой точкой.
2) Если главная часть разложения Лорана содержит конечное число членов, т.е.

то точка  называется полюсом, а число
называется полюсом, а число  называется порядком полюса. При
называется порядком полюса. При  полюс называется простым.
полюс называется простым.
|
|
|
3) Если главная часть разложения Лорана содержит бесконечное число членов, то точка  называется существенно особой точкой.
называется существенно особой точкой.
Рассмотрим поведение функции в проколотой окрестности особой точки.
Квант. 08.01.03. Поведение функции в устранимой особой точке (Т)
Рассмотрим однозначную аналитическую функцию 
Пусть 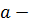 ее устранимая особая точка
ее устранимая особая точка
Тогда для этого необходимо и достаточно, чтобы в этой точке функция имела конечный предел

Доказательство.
1) Пусть 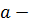 устранимая особая точка. Тогда в проколотой окрестности
устранимая особая точка. Тогда в проколотой окрестности  имеет место разложение
имеет место разложение

и, следовательно, существует конечный предел

Полагая  , мы получим функцию аналитическую в точке
, мы получим функцию аналитическую в точке  (устраним особенность).
(устраним особенность).
Обратно, пусть функция  аналитична в проколотой окрестности
аналитична в проколотой окрестности 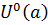 точки
точки  , и существует конечный предел
, и существует конечный предел

Следовательно, функция  ограничена в замкнутом круге
ограничена в замкнутом круге

Оценим коэффициенты главной части разложения Лорана (так же как мы оценивали коэффициенты Тейлора)

Устремляя  к нулю, получим
к нулю, получим 
 и, следовательно,
и, следовательно, 
 . Это значит, что главная часть разложения Лорана отсутствует и точка
. Это значит, что главная часть разложения Лорана отсутствует и точка  является устранимой особой точкой.
является устранимой особой точкой.
Замечание.
Полагая
 мы получим функцию аналитическую в точке
мы получим функцию аналитическую в точке  (устраним особенность).
(устраним особенность).
Пример.
 Эта функция является отношением двух аналитических функций и, следовательно, аналитична во всех точках кроме тех, где знаменатель обращается в нуль. То есть кроме точек
Эта функция является отношением двух аналитических функций и, следовательно, аналитична во всех точках кроме тех, где знаменатель обращается в нуль. То есть кроме точек  , которые являются изолированными особыми точками (в них функция не определена). Рассмотрим точку
, которые являются изолированными особыми точками (в них функция не определена). Рассмотрим точку 

Доопределим нашу функцию в этой точке, положив  Получим функцию аналитическую в точке
Получим функцию аналитическую в точке 
|
|
|

Точка  для этой функции является полюсом первого порядка (простым полюсом). Поскольку в разложении в ряд Лорана в окрестности точки
для этой функции является полюсом первого порядка (простым полюсом). Поскольку в разложении в ряд Лорана в окрестности точки  (по степеням
(по степеням  правильная часть отсутствует, а главная состоит из одного члена
правильная часть отсутствует, а главная состоит из одного члена

Вычислим предел

Это свойство (равенство предела бесконечности) является характеристическим для полюса.
 2020-05-12
2020-05-12 79
79







