Полный и дробный факторные эксперименты

Полным факторным экспериментом (ПФЭ) называется такой эксперимент, при реализации которого определяется значение параметра оптимизации при всех возможных сочетаниях уровней варьирования факторов. Если мы имеем дело с k факторами, каждый из которых устанавливается на q уровнях, то для осуществления полного факторного эксперимента необходимо произвести n=qk  опытов.

Наибольшее распространение получили эксперименты, в которых факторы варьируют на 2-х уровнях, то есть n=2k, менее популярны эксперименты типа n=3k так как с ростом числа уровней факторов резко взрастает количество опытов.

Планирование, проведение и обработка результатов ПФЭ состоит из следующих обязательных этапов:

1) кодирование факторов;

2) составление план-матрицы эксперимента;

3) рандомизация опытов;

4) реализация планов эксперимента;

5) проверка воспроизводимости опытов;

6) проверка адекватности линейной модели;

7) оценка значимости коэффициентов уравнения.

Пример: Исследуем процесс повреждения семян в комбайне.

Цель эксперимента – определить зависимость повреждаемости семян подсолнечника от частоты вращения барабана и зазоров на входе между барабаном и подбарабаньем.

Предварительные исследования позволили установить технологически разумные пределы, в которых могут изменятся факторы:

1. Частота вращения n = 350…1350 об/мин;

2. Зазор между барабаном и подбарабаньем на входе

δ = 18…23 мм.

В таблице 1 представлены факторы в закодированном виде.

Нулевой уровень x₀ – выбирают обычно в центре интервала, в котором предполагается вести эксперимент.

Таблица 1 – Кодирование факторов

Интервал варьирования и уровни факторов	Частота вращения n, об/мин	Зазор δ, мм
Нулевой уровень хi=0	850	23
Интервал варьирования δi	400	4
Нижний уровень xi= –1	450	19
Верхний уровень xi= +1	1250	27
Кодовое обозначение	x1	x2

 

 

При выборе интервала варьирования необходимо учитывать, что при оптимизации процесса вначале целесообразно описать его линейным уравнением и поэтому интервал варьирования должен быть достаточно мал для получения линейных уравнений, и в то же время достаточно велик, чтобы не получить ошибочного вывода о незначимом влиянии какого либо из факторов.

Связь между кодовым и натуральным выражением фактора задаётся формулой:

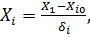                                                                        (1)

где 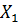 – натуральное значение фактора;

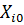     – значение i -го фактора на нулевом уровне;

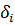     – интервал варьирования i -го фактора.

При постановке полного факторного эксперимента каждый уровень одного фактора сочетается с каждым уровнем другого. Такой план называют ортогональным планом первого порядка (рис. 1). Основным преимуществом такого плана является раздельная независимая оценка коэффициентов уравнения регрессии. Допустим, имеется двухфакторный эксперимент, в котором фактор А- (х₁) варьирует на двух уровнях: (-1) и (+1), столько же уровней имеет и фактор В- (х₂). В данном примере возможны 4 комбинации уровней, не считая повторностей каждой комбинации. Эти комбинации представлены графически вершинами квадрата, как показано на рисунке 1.

 

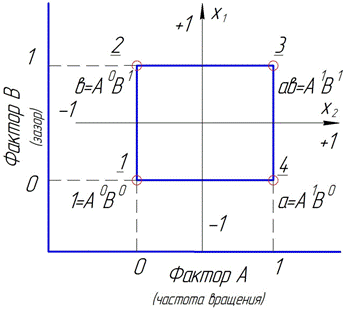
Рисунок 1 – Схема ортогонального плана первого порядка:

1, 2, 3, 4 – комбинации уровней.

Когда факторы А и В приняты на нижнем уровне, то их обозначают А ₀ В ₀=(1) или, обозначая строчными латинскими буквами, пишут а ₀ b ₀=(1). В этих случаях символ (1) есть отклик в испытании, где оба фактора на нижнем уровне.

Запись а ₀ b ₁= b соответствует условию, что фактор В на верхнем уровне, а фактор А – на нижнем уровне. Запись а ₁ b ₀= а показывает, что фактор А принят на верхнем, а фактор В – на нижнем уровне и а ₁ b ₁= аb – оба фактора на верхних уровнях.

Комбинации условий эксперимента 22 можно выразить в виде таблицы, если обозначить нижний уровень фактора –1, а верхний +1. Такая таблица называется матрицей планирования эксперимента.

Матрицей планирования эксперимента называется таблица, содержащая условия проведения всех опытов в соответствии с выбранным планом.

Матрица планирования составляется следующим образом: например, для x₁ уровни чередуются в каждом опыте для x₂ - через 2 опыта для x₃ через 4. Матрица планирования приведена в (табл. 2).

Таблица 2 – Матрица планирования ПФЭ типа 2²

Опыт	x1	x2
1	-1	-1
2	+1	-1
3	-1	+ 1
4	+1	+ 1

План эксперимента, приведенный в таблице 2, называют ортогональным планом первого порядка. Основное преимущество такого плана является раздельная (независимая) оценка коэффициентов регрессии.

Рандомизация опытов. На процесс дробления семян оказывают влияние не только факторы x₁ и x₂, но еще целый ряд факторов, которые могут быть вообще неизвестны исследователю.

Для того, чтобы внести элемент случайности влияния этих факторов на результат эксперимента, а это необходимо для обоснованного использования аппарата математической статистики, устанавливается случайный порядок постановки опытов во времени. Эта процедура называется рандомизацией. Для её осуществления используют таблицу случайных чисел или извлечения номеров из урны.

В рассматриваемом примере получили следующую последовательность проведения опытов: 2, 3, 1, 2, 4, 1, 3, 4. В этой последовательности каждое сочетание уровней (номера опытов) встречаются дважды.

Параллельные опыты предусматриваются для оценки воспроизводимости процесса и проведения статистических оценок.

Реализация плана эксперимента. Так как условились функцию отклика разложить в степенной ряд (Тейлора), то уравнение регрессии принимает вид (при k = 2):

y=b₀+b₁x₁+b₂x₂+b₁₂x₁x₂+b₁₁x₁2+b₂₂x₂2,    (7.3)

то необходимо найти 6 коэффициентов уравнения. Из них первый - свободный член. Подставим к нему фиктивный фактор и составляем полную план-матрицу эксперимента (табл. 3).

Итак, при k=2 (x₁,x₂) количество опытов n=2k=22=4 опыта, то есть в данном случае 4 строки.

Число столбцов і примем равным числу членов в уравнении.

Таблица 3 – Полная план-матрица эксперимента

u	i
	0	1	2	3	4	5
	x0	x1	x2	x1x2	x12	x22
1	+	-	-	+	+	+
2	+	+	-	-	+	+
3	+	-	+	-	+	+
4	+	+	+	+	+	+

После построения плана-матрицы это количество уточняется.

Проанализируем план-матрицу:

1. В данном примере получилось лишь 4 различных столбца. Столбцы, соответствующие квадратам факторов, неотличимы от столбца x₀.

Это общий результат для планов ПФЭ 2k – они не позволяют определить коэффициенты при x_i² эти коэффициенты входят в коэффициент b₀. Поэтому ПФЭ 2k называют планом первого порядка и позволяют определить только коэффициенты при x₀ факторах x₁…x_k и взаимодействиях x_ij. Важно отметить, что при этом апроксимирующая поверхность пройдёт через все n точек, по которым она построена.

Такие планы-матрицы ещё называют ортогональными, а планирование называется ортогональным планированием.

Основное условие ортогональности – любое произведение суммы двух различных столбцов в матрице должно быть равно 0.

Определение коэффициентов уравнения регрессии при ортогональном планировании осуществляется по следующей формуле:

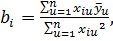                                                              (2)

в планах ПФЭ 2^k, то есть количество коэффициентов равно числу опытов.

Проведенное описание порядка построения планов ПФЭ 2^k, кодирования факторов и определение коэффициентов уравнения регрессии не изменяется от числа факторов. Приведём стандартные планы (табл. 4) и общий вид уравнения регрессии, которые могут быть построены при их реализации.

Таблица 4 – Стандартные планы

Опыты	Матрица планирования				Расширенная матрица
	х1	х2	х3	х4	x1x2	x1x3	x1x4	x2x3	x2x4	x3x4	х123	х124	х234	х134	х1234
1	-	-	-	-	+	+	+
2	+	-	-	-	-	-	-
3	-	+	-	-	-	+	+
4	+	+	-	-	+	-	-
5	-	-	+	-	+	-	+
6	+	-	+	-	-	+	-
7	-	+	+	-	-	-
8	+	+	+	-	+	-
9	-	-	-	+	+	+
10	+	-	-	+	-	-
11	-	+	-	+	-	+
12	+	+	-	+	+	-
13	-	-	+	+	+	-
14	+	-	+	+	-	+
15	-	+	+	+	-	-

Y_(∑xi=3)=b₀+b₁x₁+b₂x₂+b₃x₃+b₁₂x₁x₂+b₂₃x₂x₃+b₁₃x₁x₃+b₁₂₃x₁x₂x₃                 (3)

 

При сопоставлении планов для различных значений k привлекает внимание то обстоятельство, что включение каждого нового фактора приводит к удвоению числа опытов в плане при k =6 число опытов n =64, 2⁷=128 и т.д.

Реализация таких планов становится трудной, дорогостоящей задачей и требующей больших затрат времени эффективность ПФЭ заметно снижается. Это обстоятельство привело к идее дробного факторного эксперимента (ДФЭ) или дробной реплики ПФЭ – ДФЭ.

Даже такая информация о процессе даёт возможность предположить, что некоторые из взаимодействующих факторов незначимы в той ограниченной части факторного пространства, в которой предполагается проведение эксперимента.

Если влияние некоторого взаимодействия признаётся пренебрежимо малым, то естественно, что коэффициент регрессии при таком взаимодействии не будет значимо отличаться от нуля. Это даёт возможность использовать соответствующий столбец расширенной матрицы для оценки влияния дополнительного фактора.

Опыт	x0	x1	x2	x3	x1x2	x1x3	x2x3	x1x2x3
1	+	-	-	+	+	-	-	+
2	+	+	-	-	-	-	+	+
3	+	-	+	-	-	+	-	+
4	+	+	+	+	+	+	+	+

          

То есть строится план ПФЭ для меньшего числа факторов:

2k-р,                                                                (4)

где р – количество взаимодействий в ПФЭ заменённое новыми факторами.

В полученной матрице имеются одинаковые столбцы, а это значит, что соответствующие коэффициенты неразличимы и можно судить лишь об их совместной величине. В данном случае b₀ неотличим от b₁₂₃, b₁ от b₂₃, b₂ от b₁₃ и b₃ от b₁₂. Получены смешанные оценки коэффициентов. Это не представляет опасности, если есть уверенность в том, что эффекты взаимодействия факторов равны нулю и тогда найдено то, что искали. Если же такой уверенности нет, то необходимо перейти к плану ПФЭ.

 

ДФЭ 2^3-1 – полуреплика.

2 ^5-2 – четверть реплика.

ДФЭ очень удобны при большом числе факторов (k > = 5).

Планы ПФЭ и ДФЭ позволяют найти коэффициенты в уравнении регрессии, если аппроксимируется поверхность хорошо описывается полиномом без квадратичных членов. Полученную модель можно использовать для прогнозирования значения отклика, и при любых значениях факторов, сходящихся внутри области определения факторов.

Для пояснения сказанного вернёмся к предыдущему примеру, то есть определим зависимость повреждаемости семян в комбайне от частоты вращения барабана и зазора между барабаном и подбарабаньем на входе при обмолоте подсолнечника.

Были приняты уровни факторов согласно таблице 1 и получены в результате проведения опытов значения функции отклика (таблица 5).

Таблица 5 - План-матрица

Опыт	х0	х1	х2	х12	у1	у2	у3	y	~ y
1	+	-	-	+	12	18	18	16	16
2	+	+	-	-	36	30	30	32	32
3	+	-	+	-	5	7	12	8	8
4	+	+	+	+	16	30	26	24	24

 

Вид уравнения регрессии необходимо получить следующий:

y = b 0 + b₁х1 + b 2 X 2 + b₁₂Х1Х 2.                            (5)

Определяем коэффициенты уравнения регрессии по известному соотношению (3):

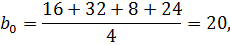
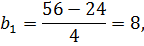
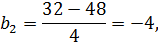
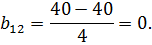
таким образом, получен полином:

y= 20+8 x₁- 4 x₂.                           (6)

Решая уравнение относительно x₁ и x₂, получаем значение y, предсказанное уравнением, и видим, что получаемые значения равны экспериментальным. То есть, полученное уравнение адекватно описывает аппроксимируемую поверхность. Для проверки этого положения необходимо провести опыт в центре плана при х₁ и х₂ = 0.

Если полученный результат будет равен b ₀ или иметь малые расхождения, то модель приемлема и на этом заканчивается первый этап исследований.

Если необходимо получить уравнение регрессии в натуральных переменных, необходимо раскодировать уравнение (6) с учётом соотношения (7.2):

В результате преобразований получим:

P = 26+0,02 n - δ.                                     (7)

Проводится проверка воспроизводимости опытов, оценка значимости коэффициентов регрессии, а также проверка адекватности линейной модели:

а) проверка воспроизводимости опытов осуществляется по критерию Кохрена:

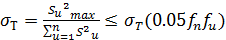                                                  (8)

где      f _n = n - число независимых оценок опытов (количество опытов);

     f _u = m –1 – число степеней свободы;

    S _u² – дисперсия, характеризующая рассеяние результатов опытов;

    m - число повторностей,

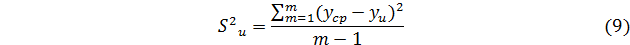
Процесс воспроизводим, если выполняется неравенство по критерию Кохрена (8).

б) оценка значимости коэффициентов регрессии производится с помощью критерия Стьюдента:

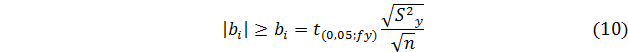
где  – табличное значение коэффициента Стьюдента;

S _y² – дисперсия воспроизводимости (ошибки опыта) определяется по формуле:

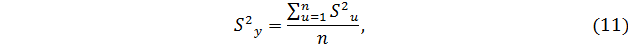
Полученные по расчету коэффициенты регрессии значимы, если выполняется условие по критерию Стьюдента (7.12).

в) проверка адекватности  линейной модели  выполняется  с помощью критерия Фишера:

 

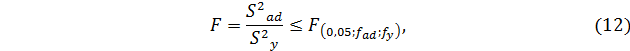
где 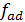 - число степеней свободы дисперсии адекватности;

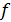 - число степеней свободы дисперсии воспроизводимости;

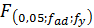- табличное значение критерия Фишера при 5% уровне значимости;

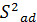 – дисперсия адекватности.

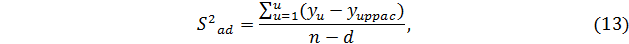
где 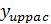   – расчетное значение отклика в u -м опыте;

d - число определяемых коэффициентов модели.

Модель адекватна, если выполняется условие по критерию Фишера.

Возникают случаи, когда имеется кривизна поверхности и она порождена не взаимодействием факторов, а нелинейностью сечений y = f₂ (x₁) при х ₂ = const, или наоборот. В общем случае линейная модель представляет собой гиперплоскость в (k +1)- мерном факторном пространстве, что исключает возможность зрительного восприятия соответствующего геометрического образа, кроме случая, когда k =2, который иллюстрируется рисунком 7.2, а. Точки 1, 2, 3 и 4 соответствуют координатам опытов при постановке полного факторного эксперимента типа 2². Из этих точек проведены прямые параллельные оси у, и на них отложены отрезки, равные значению откликов в соответствующем опыте (рис. 2).

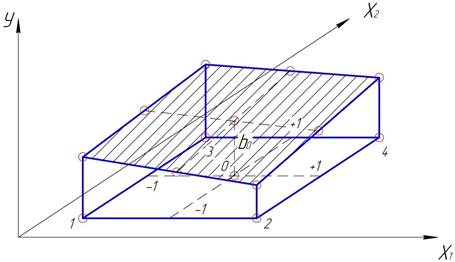
Рисунок 2 – Графическая интерпретация: гиперплоскость в

(k+1)-мерном факторном пространстве, когда k=2.

 

Как видно из рисунка 2, свободный член b ₀ в линейном уравнении регрессии численно равен значению отклика при х ₁= х ₂=0.

В этом случае аппроксимация неполным квадратичным уравнением может оказаться неудовлетворительной. Это можно обнаружить, поставив дополнительный опыт в нулевой точке.

Итак, признак невозможности использования плана ПФЭ – нелинейность каких-либо сечений поверхности отклика.

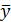Косвенный сигнал об этом несоответствии – расхождение между значениями и 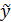в нулевой точке плана.

 

Контрольные вопросы:

1.Что такое планирование эксперимента?

2.Какова цель планирования эксперимента?

3.Какие существуют основные методы планирования?

4.Что такое полный факторный эксперимент?

5.Как проводится кодирование факторов?

6.Как составить матрицу планирования?

7.Как проводится реализация плана эксперимента?

8.Как определяются коэффициенты регрессии при ортогональном планировании?

9.Что такое дробный факторный эксперимент?

10.Что такое уравнение регрессии?

11. Какие требования к факторам?

12. Какие требования к функции отклика?

Уважаемые обучающиеся, в процессе изучения дисциплины Вам необходимо выполнить расчетно-графическую работу "Планирование, проведение и обработка результатов многофакторного эксперимента".
Методические указания по которой представлены отдельным файлом.