В связи с этим интеграл и получил свое название от латинского слова integer (целый)
 Рассмотрим примеры решения задач.
Рассмотрим примеры решения задач.
Задача 1.
Дано: АВСD – правильная пирамида, АВ =3; AD=  . Найти: а) Sосн; б) АО; в) DO г) V.
. Найти: а) Sосн; б) АО; в) DO г) V.
Решение:
а)  (используется формула для вычисления площади правильного треугольника)
(используется формула для вычисления площади правильного треугольника)
АВ = 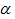 = 3, имеем
= 3, имеем 
б)  (формула радиуса описанной окружности через сторону правильного треугольника)
(формула радиуса описанной окружности через сторону правильного треугольника)  .
.


Задача 2.
Дано: АВСDF – правильная пирамида, 
Решение:
1) Рассмотрим  следовательно,
следовательно, 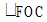 – равнобедренный, ОС = FО = 2.
– равнобедренный, ОС = FО = 2.

Решить задачу №696
| А |
| В |
| С |
| D |
Основанием пирамиды DABC является треугольник, в котором АВ=20см, АС=29см, ВС=21см. Грани DAB и DAC перпендикулярны к плоскости основания, а грань DBC составляет с ней угол в 60о Найдите объем пирамиды.
Решение
В треугольнике АВС: 
 , следовательно, треугольник АВС-прямоугольный.
, следовательно, треугольник АВС-прямоугольный.
АВ перпендикулярно ВС, DB-наклонная, АВ-её проекция, следовательно DB перпендикулярно к ВС (по теореме о трех перпендикулярах), т.е. треугольник DBC-прямоугольный. 
Задача 3.
Смолу для промышленных нужд собирают, подвешивая конические воронки к соснам. Сколько воронок диаметром 10 см с образующей 13см нужно собрать, чтобы заполнить 10-
литровое ведро?
Ответ:~ 32 воронки
Самостоятельная работа
Задача№1
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Задача №2
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30°.
Задача №3
| D |
| С |
| О |
| 6 |
| 8 |
АС=6, ВС=8. Каждое боковое ребро составляет с плоскостью основания угол 45º. Найти: V
| В |
| A |
Контрольные вопросы.
1) Формула объёма пирамиды?
2) Формула объёма конуса?
 2020-06-08
2020-06-08 95
95







