Наличие седловой точки

 

Определение 3.1.

Нижней оценкой цены игры называется величина ;    верхней оценкой цены игры называется величина .

Лемма 3.1. Справедливо соотношение a ≤ b.

Для доказательства леммы представим игру G (m ´ n)в матричной формев виде табл. 3.4.

Таблица 3.4

Bj Ai	B 1	…	Bj	…	Bk	…	Bn
A 1	a 11	…	a 1 j	…	a 1 k	…	a 1 n
…	…	…	…	…	…	…	…
Ai	ai 1	…	aij	…	aik	…	ain
…	…	…	…	…	…	…	…
Al	a 11	…	alj	…	alk	…	ain
…	…	…		…		…	…
Am	am 1	…	amj	…	amk	…	amn

 

Пустьa= a_jk, b= a_lj. Из определения верхней и нижней границ следует, что элемент a_jk является минимальным в i -й строке, т.е. a= a_jk ≤ a_jj, а элемент a_lj является максимальным в j -м столбце, т.е. a_jj ≤ a_lj =b. Лемма доказана.

Определение 3.2. Если a=b= V, то игра имеет седловую точку, стратегии A_i, B_j, при которых достигается выигрыш V, называются оптимальными чистыми стратегиями, а пара стратегий (A_i, B_j) называется решением игрыG (m ´ n).

Решение игры обладает свойством устойчивости (равновесия), т.е. если один из игроков придерживается своей оптимальной стратегии, то другому игроку не выгодно отходить от своей, так как его положение при этом может только ухудшиться. Из леммы 3.1 непосредственно следует, что признаком наличия седловой точки является нахождение в матрице игры такого элемента a_ij, который является одновременно минимальным в i -й строке и максимальным в j -м столбце. Если такой элемент не единственный, то игра имеет не единственное решение, но все решения равнозначны, т.е. дают выигрыш, равный цене игры V.

Теорема 3.1 [6]. Антагонистическая игра с полной информацией имеет седловую точку.

Таким образом, для любой антагонистической игры с полной информацией существует решение – пара чистых стратегий , дающих игроку А устойчивый выигрыш a_ij = V. Наличие нескольких седловых точек означает существование нескольких решений, но все они дают один и тот же выигрыш, равный цене игры V.

Рассмотрим в качестве примера матричную игру G (2´4)с полной информацией, представленную табл. 3.3. Дополним данную таблицу новыми строкой и столбцом, получив табл. 3.5.

Таблица 3.5

Bj Ai
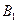
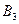
A 1	4	–5	4	–5	–5
A 2	–5	6	6	–5	–5
	4	6	6	–5

 

Из таблицы видно, что , .

Имеем две седловые точки a ₁₄и a ₂₄,соответствующие решениям(A ₁, B ₄)и(A ₂, B ₄)с ценой игры V = –5.

Вернемся теперь к матричной игре G (2´2)с неполной информацией, представленной в табл. 3.2. Аналогично предыдущему примеру дополним табл. 3.2 до табл. 3.6.

Таблица 3.6

Bj Ai
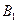
A 1	4	–5	–5
A 2	–5	6	–5
	4	6

 

Для данной таблицы , , т.е. a< b.Седловая точка, а, следовательно, и решение в чистых стратегиях, отсутствуют.

3.3. Методы решения матричных игр
при отсутствии седловой точки

Смешанные стратегии

В случае отсутствия седловой точки, в качестве решения игры используются так называемые смешанные стратегии

,

где p_i и q_j – вероятности выбора стратегий A_i и B_j игроками A и B соответственно. Решением игры в данном случае является пара оптимальных смешанных стратегий (S_A^*, S_B^*), максимизирующих математическое ожидание цены игры (средний выигрыш).

Теорема 3.2 [6]. Любая антагонистическая игра имеет хотя бы одно оптимальное решение, т.е., пару в общем случае смешанных стратегий (S_A^*, S_B^*), дающих игроку А устойчивый выигрыш, равный цене игры V,α ≤ V ≤ β.

Чистую стратегию можно рассматривать как частный случай смешанной стратегии, когда одна вероятность имеет единичное значение, а все остальные – нулевое.

Рассмотрим матричную игру G (m ´ n), не имеющую седловой точки, для которой необходимо найти решение – пару оптимальных смешанных стратегий S_A =(p ₁, p ₂, …, p_m)и S_B =(q ₁, q ₂, …, q_n) и соответствующую цену игры V.

Предварительно следует попытаться упростить матрицу игры. Для этого вводятся отношения предпочтения (доминирования) и безразличия (дублирования) на множестве стратегий.

Определение 3.3:

· стратегия A_i предпочтительнее стратегии A_k (доминирует A_k) (обозначается ), если все выигрыши, указанные в i -й строке матрицы игры, не меньше соответствующих выигрышей k -й строки, или формально ;

· стратегии A_i и A_k находятся в отношении безразличия (дублирования) (обозначается A_i» A_k), если все выигрыши, указанные в i -й строке матрицы игры, совпадают с соответствующими выигрышами k -й строки, или формально ;

· стратегия B_j предпочтительнее стратегии B_r (доминирует B_r) (обозначается ), если все выигрыши, указанные в j -м столбце матрицы игры, не меньше соответствующих выигрышей r -го столбца, или формально ;

· отношение безразличия для стратегий игрока B вводится аналогично игроку A, т.е. .

Можно доказать следующую лемму [5].

Лемма 3.2. Для игры G (m ´ n)число активных стратегий игроков равно min { m, n }. Другими словами, если, например, m>n, то в оптимальной стратегии S_A =(p ₁, p ₂, …, p_m) игрока A будет не более n отличных от нуля вероятностей p_i.

Таким образом, предварительным этапом решения матричной игры является ее упрощение, т.е. удаление из матрицы доминируемых и дублируемых стратегий.

Рассмотрим данный этап на примере матричной игры G (5´5), представленной табл. 3.7.

Таблица 3.7

Bj Ai	B 1	B 2	B 3	B 4	B 5
A 1	4	7	2	3	4
A 2	3	5	6	8	9
A 3	4	4	2	2	8
A 4	3	6	1	2	4
A 5	3	5	6	8	9

 

Так как справедливы соотношения , , , , , то удалим доминируемые и дублируемые стратегии A ₄, A ₅, B ₂, B ₄, B ₅.

В полученной матрице снова проведём удаление, так как . Получим упрощенную игру G (2´2), представленную табл. 3.8.

Таблица 3.8

Bj Ai	B 1	B 3
A 1	4	2
A 2	3	6

 

Нетрудно убедиться, что данная игра не имеет седловой точки и необходимо искать решение в смешанных стратегиях.

После упрощения игры следующим (основным) этапом является поиск оптимального решения в виде смешанных стратегий (S_A, S_B), применяя точные или приближенные методы.

Метод Лагранжа

Метод Лагранжа относится к точным методам решения матричных игр G (m ´ m), т.е. имеющим квадратные матрицы (или приведенные к такому виду после упрощения).

Допустим, что игрок A использует смешанную стратегию S_A =(p ₁, …, p_m), а игрок B отвечает своей чистой стратегией B_i (i =1, 2, …, m). Цена игры в таком случае равна . Если же игрок B также будет применять смешанную стратегию S_B =(q ₁, …, q_m), то итоговая цена игры будет равна

.       (3.1)

Для нахождения оптимального решения необходимо максимизировать значение V при ограничениях .

Составим функцию Лагранжа L = V + l₁(p ₁ + … + p_m – 1) + l₂(q ₁ + … + q_m – 1) и приравняем к нулю частные производные по всем аргументам: .

В результате получим следующую систему из (2 m + 2)уравнений с (2 m + 2) неизвестными:

Решение этой системы и даёт смешанные стратегии для обоих игроков.

Нетрудно заметить, что исходная система уравнений включает две независимые подсистемы (для p_i, i =1, …, m, l₁ и q_j, j =1, …, m, l₂ соответственно), состоящие из (m + 1)уравнений с (m + 1)неизвестными, решение которых и даст искомые вероятности p_i и q_j, а также после подстановки этих вероятностей в формулу (3.1) цену игры V.

В качестве примера рассмотрим игру G (2´2), представленную в общем виде табл. 3.9.

Таблица 3.9

Bj Ai	B 1	B 2
A 1	a 11	a 12
A 2	a 21	a 22

 

V ₁ = a ₁₁ p ₁ + a ₂₁ p ₂, V ₂ = a ₁₂ p ₁ + a ₂₂ p ₂,

V = V ₁ q ₁ + V ₂ q ₂ = (a ₁₁ p ₁ + a ₂₁ p ₂) q ₁ + (a ₁₂ p ₁ + a ₂₂ p ₂) q ₂.

L = V + l₁(p ₁ + p ₂ – 1) + l₂(q ₁ + q ₂ – 1).

Приравняв к нулю частные производные функции Лагранжа по всем аргументам, получим следующую систему уравнений:

Решив данную систему получим следующие значения вероятностей:

.

Подставив полученные значения в выражение для V, получим цену игры.

Например, для игры G (2´2), представленной табл. 3.8, получим:

p ₁=0,6; p ₂=0,4; q ₁=0,8; q ₃=0,2; V =3,6.

Можно также найти решение в общем виде для игры G (3´3)и т.д.

Приведем более универсальный и достаточно легко компьютеризируемый способ решения матричных игр методом Лагранжа.

Рассмотрим игру игры G (3´3) в общем виде, представленную табл. 3.10.

Таблица 3.10

Bj Ai	B1	B 2	B 3
A 1	a 11	a 12	a 13
A 2	a 21	a 22	a 23
A 3	a 31	a 32	a 33

 

Для нахождения решения в смешанных стратегиях необходимо решить следующую систему уравнений:

Эту систему можно представить следующим образом:

.

Решением в общем виде представляется системой

Более конкретно:

 

Обозначив

k = – a ₁₁ a ₂₂ + a ₁₁ a ₃₂ + a ₁₁ a ₂₃ – a ₁₁ a ₃₃ + a ₂₁ a ₁₂ – a ₂₁ a ₃₂ –

 – a ₂₁ a ₁₃ + a ₂₁ a ₃₃ – a ₃₁ a ₁₂ + a ₃₁ a ₂₂ + a ₃₁ a ₁₃ – a ₃₁ a ₂₃ –

 – a ₁₂ a ₂₃ + a ₁₂ a ₃₃ + a ₂₂ a ₁₃ – a ₂₂ a ₃₃ – a ₃₂ a ₁₃ + a ₃₂ a ₂₃,

получим итоговое решение:

p ₁ = (– a ₂₁ a ₃₂ + a ₂₁ a ₃₃ + a ₃₁ a ₂₂ – a ₃₁ a ₂₃ – a ₂₂ a ₃₃ + a ₃₂ a ₂₃) / k

p ₂ = (   a ₁₁ a ₃₂ – a ₁₁ a ₃₃ – a ₃₁ a ₁₂ + a ₃₁ a ₁₃ + a ₁₂ a ₃₃ – a ₃₂ a ₁₃) / k

p ₃ = (– a ₁₁ a ₂₂ + a ₁₁ a ₂₃ + a ₂₁ a ₁₂ – a ₂₁ a ₁₃ – a ₁₂ a ₂₃ + a ₂₂ a ₁₃) / k

q ₁ = (– a ₁₂ a ₂₃ + a ₁₂ a ₃₃ + a ₂₂ a ₁₃ – a ₂₂ a ₃₃ – a ₃₂ a ₁₃ + a ₃₂ a ₂₃) / k

q ₂ = (   a ₁₁ a ₂₃ – a ₁₁ a ₃₃ – a ₂₁ a ₁₃ + a ₂₁ a ₃₃ + a ₃₁ a ₁₃ – a ₃₁ a ₂₃) / k

q ₃ = (– a ₁₁ a ₂₂ + a ₁₁ a ₃₂ + a ₂₁ a ₁₂ – a ₂₁ a ₃₂ – a ₃₁ a ₁₂ + a ₃₁ a ₂₂) / k

V = – |A| / |A 1 |,

где А — исходная матрица игры.

Данный подход легко применим для произвольной игры G (m ´ m): строится матрица A 1, далее, используя определители, записываются выражения для p_i и q_j, множитель знака для них будет равен (– 1) ^{m + i + 1}.