Энергетические зоны в одномерном случае
Общие выводы можно проиллюстрировать в одномерном случае при двукратном вырождении. В отсутствие взаимодействия 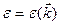 дается рис. 5.4 а. В первом порядке по слабому потенциалу
дается рис. 5.4 а. В первом порядке по слабому потенциалу  эта функция остается неизменной всюду, кроме окрестности брэгговских плоскостей. Если волновой вектор принимает значение близкое к брэгговской плоскости, т.е. близка к точке ½
эта функция остается неизменной всюду, кроме окрестности брэгговских плоскостей. Если волновой вектор принимает значение близкое к брэгговской плоскости, т.е. близка к точке ½ 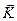 , то для нахождения измененных значений энергетических уровней, построим параболу в точке
, то для нахождения измененных значений энергетических уровней, построим параболу в точке 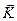 (рис. 5.4 б). Вырождение в точке пересечения снимается, при этом в данной точке возникает расщепление, равное 2
(рис. 5.4 б). Вырождение в точке пересечения снимается, при этом в данной точке возникает расщепление, равное 2  (рис. 5.4 в). В результате исходная кривая для свободных электронов принимает вид рис. 5.4 г.
(рис. 5.4 в). В результате исходная кривая для свободных электронов принимает вид рис. 5.4 г.
При учете всех брэгговских плоскостей приходим к совокупности кривых, изображенных на рис. 5.4 д. Этот способ представления электронных уровней в периодическом потенциале называется схемой расширенных зон.
Если задавать все уровни векторами  из первой зоны Бриллюэна, то можно перенести кусочки кривых на рис. 5.4, д в первую зону, проделав смещение на вектор обратной решетки (рис.5.4, е). Это представление называется схемой приведенных зон.
из первой зоны Бриллюэна, то можно перенести кусочки кривых на рис. 5.4, д в первую зону, проделав смещение на вектор обратной решетки (рис.5.4, е). Это представление называется схемой приведенных зон.
Можно также подчеркнуть периодичность описания в  -пространстве, продолжив периодически рис. 5.4, е на все
-пространстве, продолжив периодически рис. 5.4, е на все  -пространство. В результате получим рис. 5.4, ж, на котором видно, что всякий уровень с заданным
-пространство. В результате получим рис. 5.4, ж, на котором видно, что всякий уровень с заданным  может быть описан и другими волновыми векторами, отличающимися от
может быть описан и другими волновыми векторами, отличающимися от  на любой из векторов обратной решетки. Такое представление называется схемой повторяющихся зон. Схема повторяющихся зон является наиболее общим представлением, но такое описание избыточно – каждый уровень показан много раз для всех эквивалентных волновых векторов
на любой из векторов обратной решетки. Такое представление называется схемой повторяющихся зон. Схема повторяющихся зон является наиболее общим представлением, но такое описание избыточно – каждый уровень показан много раз для всех эквивалентных волновых векторов  ,
, 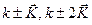 и т.д.
и т.д.
Энергетическая щель
В общем случае слабый периодический потенциал приводит к энергетической щели вблизи брэгговских плоскостей. Действительно, если  , то при пересечении волновым вектором брэгговских плоскостей, совершается непрерывный переход с одной ветви на другую, как показано на рис. 5.4, б. Если
, то при пересечении волновым вектором брэгговских плоскостей, совершается непрерывный переход с одной ветви на другую, как показано на рис. 5.4, б. Если  , то это уже не так. Теперь при переходе волнового вектора через брэгговскую плоскость энергия изменяется непрерывно только в том случае, если мы остаемся на кривой, отвечающей нижней или верхней ветви (рис. 5.4, в). Чтобы перейти с одной ветви на другую при непрерывном изменении
, то это уже не так. Теперь при переходе волнового вектора через брэгговскую плоскость энергия изменяется непрерывно только в том случае, если мы остаемся на кривой, отвечающей нижней или верхней ветви (рис. 5.4, в). Чтобы перейти с одной ветви на другую при непрерывном изменении  , энергия должна изменяться скачком по крайней мере на величину 2
, энергия должна изменяться скачком по крайней мере на величину 2  .
.
Число уровней в зоне
Рассмотрим одномерный (линейный кристалл) с постоянной решетки, равной  ; такой кристалл построен из
; такой кристалл построен из 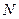 элементарных ячеек длиной
элементарных ячеек длиной  . Чтобы подсчитать число возможных состояний введем периодические граничные условия для волновых функций, а именно, длину блока периодичности будем считать равной длине цепочки. Разрешенные значения волнового вектора электрона в первой зоне Бриллюэна принимают значения:
. Чтобы подсчитать число возможных состояний введем периодические граничные условия для волновых функций, а именно, длину блока периодичности будем считать равной длине цепочки. Разрешенные значения волнового вектора электрона в первой зоне Бриллюэна принимают значения:
 (5.34)
(5.34)
Этот ряд ограничен значением  , поскольку
, поскольку  служит границей зоны Бриллюэна. Таким образом, полное число значений
служит границей зоны Бриллюэна. Таким образом, полное число значений  точно равно
точно равно 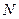 - числу элементарных ячеек. Отсюда следует, что каждая элементарная ячейка в каждой энергетической зоне дает точно одно независимое значение
- числу элементарных ячеек. Отсюда следует, что каждая элементарная ячейка в каждой энергетической зоне дает точно одно независимое значение  . Это утверждение переносится и на случай трех измерений. С учетом того, что каждый электрон может иметь одну из двух спиновых ориентаций, общее число независимых состояний (орбиталей) в каждой энергетической зоне равно 2
. Это утверждение переносится и на случай трех измерений. С учетом того, что каждый электрон может иметь одну из двух спиновых ориентаций, общее число независимых состояний (орбиталей) в каждой энергетической зоне равно 2 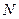 .
.
Если на каждую элементарную ячейку приходится один атом одновалентного элемента, то в энергетической зоне будет занято электронами ровно половина состояний (уровней). Если кристалл состоит из атомов двухвалентного элемента, и каждый атом может отдать два электрона, то зона будет заполнена целиком.
Пусть в элементарной ячейке кристалла Z электронов. Тогда общее число электронов в решетке равно zN. При достаточно низкой температуре они займут первые zN энергетических уровней. Таким образом, число заполненных зон равно  .
.
Если 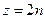 (четное число), то все зоны, содержащие электроны, полностью ими заполнены, энергия Ферми совпадает с верхней границей одной из зон.
(четное число), то все зоны, содержащие электроны, полностью ими заполнены, энергия Ферми совпадает с верхней границей одной из зон.
Металлы и диэлектрики. Если валентные электроны заполняют целиком одну или более верхних разрешенных зон, то кристалл является диэлектриком. В таком кристалле наложение внешнего электрического поля не приводит к появлению электрического тока. Если целиком заполненная зона отделена от следующей более высокой зоны энергетической щелью, то нет никакого способа непрерывным образом изменить суммарный импульс электронов кристалла. Все разрешенные состояния заняты и наложение поля ничего не может изменить. Ситуация совсем иная, чем в случае свободных электронов (смещение сферы Ферми в электрическом поле).
Другой подход к анализу этой ситуации состоит в использовании уравнения движения:
 . (5.35)
. (5.35)
Под действием постоянной силы волновой вектор электрона будет непрерывно увеличиваться с течением времени. Но когда  , возрастая, достигнет границы зоны, волновой вектор испытает «переброс» (рис.5.5) на противоположную границу.
, возрастая, достигнет границы зоны, волновой вектор испытает «переброс» (рис.5.5) на противоположную границу.
Это движение будет происходить вновь и вновь, но не приведет к какому-либо результирующему ускорению, в чем можно убедиться, если провести усреднение по всем состояниям зоны.
Любой кристалл может быть диэлектриком при четном числе валентных электронов в элементарной ячейке кристалла.
Если в кристалле число валентных электронов на элементарную ячейку четное, то необходимо отдельно рассматривать случаи перекрывающихся и неперекрывающихся энергетических зон. Если зоны перекрываются, то вместо одной заполненной зоны, характерной для диэлектрика, мы можем иметь две или более частично заполненных зон, приводящих к тому, что кристалл обнаруживает свойства металла (рис. 5.6).
Рис. 5.6, а рис. 5.6, б рис. 5.6, в
В щелочных и благородных металлах на элементарную ячейку приходится один валентный электрон; и поэтому они являются металлами. Редкоземельные металлы имеют по два валентных электрона на элементарную ячейку и могли бы быть диэлектриками, но энергетические зоны у них перекрываются, поэтому они металлы, хотя и не очень хорошие. Кристаллы алмаза, кремния и германия имеют по два четырехвалентных атома на элементарную ячейку. Энергетические зоны в них не перекрываются, и поэтому чистые кристаллы при абсолютном нуле являются диэлектриками.
Наивысшая из заполненных зон при абсолютном нуле называется валентной зоной, наинизшая из незаполненных зон – зоной проводимости. Верхнюю границу валентной зоны принято обозначать через  , а нижнюю границу зоны проводимости – через
, а нижнюю границу зоны проводимости – через  ; ширину запрещенной зоны
; ширину запрещенной зоны  (рис. 5.7).
(рис. 5.7).
Рис. 5.7.
При  лишь немногие электроны получают в результате тепловой флуктуации энергию достаточную для перехода его в зону проводимости (диэлектрики).
лишь немногие электроны получают в результате тепловой флуктуации энергию достаточную для перехода его в зону проводимости (диэлектрики).
При  в зоне проводимости появляется заметное число электронов, а в валентной зоне образуются свободные места – дырки.
в зоне проводимости появляется заметное число электронов, а в валентной зоне образуются свободные места – дырки.
В проводимости металла участвуют только электроны зоны проводимости, имеющие энергию, близкую к энергии Ферми.
В полупроводниках в проводимости участвуют электроны обеих зон - проводимости и валентной. При наличии малого числа свободных мест в валентной зоне обычно говорят не о движении многих электронов, а о движении свободных мест – дырок и соответственно о дырочной проводимости в валентной зоне наряду с электронной в зоне проводимости. Стремясь занять наинизшее энергетическое состояние, электроны в зоне проводимости полупроводника располагаются вблизи ее дна. Дырки в валентной зоне по той же причине сосредоточиваются вблизи потолка валентной зоны.
Строение поверхности Ферми
Мы уже встречались с поверхностью Ферми, как поверхностью постоянной энергии  в
в  -пространстве. Поверхность Ферми отделяет незаполненные состояния (орбитали) от заполненных. При абсолютном нуле температур большинство электронных свойств металлов определяется именно формой поверхности Ферми.
-пространстве. Поверхность Ферми отделяет незаполненные состояния (орбитали) от заполненных. При абсолютном нуле температур большинство электронных свойств металлов определяется именно формой поверхности Ферми.
Интерпретация поверхности Ферми. Формула Брэгга, определяющая границу зон, имеет вид  , откуда следует
, откуда следует
 . (5.36)
. (5.36)
Эта формула удовлетворяется значениями  , оканчивающимися в плоскости, нормальной к вектору
, оканчивающимися в плоскости, нормальной к вектору 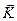 и проходящими через его середину.
и проходящими через его середину.
Первая зона Бриллюэна квадратной решетки получается как область, заключенная между взаимно перпендикулярными прямыми, проходящими через середины кратчайших векторов обратной решетки  и еще трех векторов, эквивалентных
и еще трех векторов, эквивалентных  по симметрии (рис. 5.8, а).
по симметрии (рис. 5.8, а).
Рис. 5.8, а. рис. 5.8, б.
Таким образом, первая зона Бриллюэна (элементарная ячейка Вигнера-Зейтца для обратной решетки) это совокупность точек в  -пространстве, которых можно достичь из начальной точки, не пересекая ни одной брэгговской плоскости. Для построения первой зоны Бриллюэна нужны четыре вектора обратной решетки; если постоянная решетки равна
-пространстве, которых можно достичь из начальной точки, не пересекая ни одной брэгговской плоскости. Для построения первой зоны Бриллюэна нужны четыре вектора обратной решетки; если постоянная решетки равна  , то эти четыре вектора суть
, то эти четыре вектора суть  .
.
Вторая зона Бриллюэна строится при помощи вектора  и еще трех векторов, эквивалентных
и еще трех векторов, эквивалентных  по симметрии (рис. 5.8, б). Аналогично строится третья зона. Числа 1, 2, 3 написаны на участках, относящихся к соответствующей по номеру зоне, одновременно эти числа (в порядке возрастания) отвечают векторам обратной решетки
по симметрии (рис. 5.8, б). Аналогично строится третья зона. Числа 1, 2, 3 написаны на участках, относящихся к соответствующей по номеру зоне, одновременно эти числа (в порядке возрастания) отвечают векторам обратной решетки  ,
,  ,
,  возрастающей длины. Вторую зону Бриллюэна можно определить так – совокупность точек, которых можно достичь из первой зоны, если пересечь всего одну брэгговскую плоскость. Соответственно (n + 1) зону Бриллюэна можно определить как совокупность точек, лежащих вне (n - 1) зоны, которую можно достичь из n-зоны, пересекая всего лишь одну брэговскую плоскость.
возрастающей длины. Вторую зону Бриллюэна можно определить так – совокупность точек, которых можно достичь из первой зоны, если пересечь всего одну брэгговскую плоскость. Соответственно (n + 1) зону Бриллюэна можно определить как совокупность точек, лежащих вне (n - 1) зоны, которую можно достичь из n-зоны, пересекая всего лишь одну брэговскую плоскость.
Поверхность Ферми для свободных электронов. Поверхность Ферми для свободных электронов при некоторой произвольной концентрации электронов изображена на рис. 5.9 (случай плоской квадратной решетки).
Рис. 5.9 рис. 5.10, а рис. 5.10, б рис. 5.10, в
Окружность описывает поверхность постоянной энергии для свободных электронов. Ее площадь зависит только от концентрации электронов и не зависит от взаимодействия с решеткой. Форма поверхности зависит от взаимодействия и не будет иметь форму окружности.
Тот факт, что части поверхности Ферми, относящиеся к одной зоне (например, второй) оказываются отдаленными одна от друга, представляется неудобным. Это можно поправить, перейдя к схеме приведенной зоны. Переместив треугольники, помеченные цифрой 2 на вектор обратной решетки, они окажутся внутри первой зоны Бриллюэна (рис. 5.10, б). Части поверхности Ферми из второй зоны теперь соединятся, как показано на рис. 5.11.
Рис.5.11. Изображение трех зон.
Переместив третью зону внутрь квадрата, мы придем к тому, что части поверхности Ферми из третьей зоны еще будут выглядеть разъединенными. Если взглянуть на эту картину с точки зрения периодической зонной схемы (рис. 5.12), поверхность Ферми образует розетку.
Рис. 5.12. Поверхность Ферми Рис. 5.13. Влияние слабого периодического
в третьей зоне Бриллюэна. потенциала на поверхность Ферми (рис. 5.11).
Для перехода от поверхности Ферми для свободных электронов к поверхности для почти свободных электронов необходимо учесть следующие четыре факта:
а) Взаимодействие электрона с периодическим потенциалом кристалла приводит к появлению энергетических щелей на зонных границах.
б) Почти вся поверхность Ферми будет пересекать границы зоны перпендикулярно.
в) Внутрикристаллический потенциал будет особенно сказываться в «острых углах» поверхности Ферми.
г) Полный объем, охватываемый поверхностью Ферми, зависит только от концентрации электронов и не зависит от деталей их взаимодействия с решеткой. Для количественных утверждений необходимы детальные расчеты, но можно ожидать качественно, что поверхности Ферми, относящиеся ко второй и третьей зонам Бриллюэна (рис.5.11), под влиянием слабого внутрикристаллического поля испытают изменения, характер которых можно усмотреть из рис. 5.13.
Приближенное построение поверхностей Ферми, исходя из поверхности для свободных электронов, весьма полезно. Построение поверхности Ферми для свободных электронов легко выполнить, пользуясь процедурой, предложенной Харрисоном (рис. 5.14).
Рис. 5.14. Построение Харрисона поверхности Ферми для свободных электронов во второй, третьей и четвертой зонах.
Сначала определяются точки обратной решетки, затем радиус сферы для свободных электронов. Этим радиусом проводим окружности с центром в точках обратной решетки. Каждая точка в  -пространстве, которая лежит внутри по крайней мере одной из сфер, соответствует занятому состоянию в первой зоне Бриллюэна. Точки, лежащие по меньшей мере в двух сферах, соответствуют занятым состояниям во второй зоне; аналогично для точек, лежащих в трех и более сферах.
-пространстве, которая лежит внутри по крайней мере одной из сфер, соответствует занятому состоянию в первой зоне Бриллюэна. Точки, лежащие по меньшей мере в двух сферах, соответствуют занятым состояниям во второй зоне; аналогично для точек, лежащих в трех и более сферах.
 2020-06-29
2020-06-29 439
439






