2020-10-10
505
Когда число наблюдений небольшое (n ≤30), а все частоты в вариационном ряду р =1, применяется формула:
,
где d – истинные отклонения вариант от истинной средней (V – М).
При р >1 используется формула:
При большом числе наблюдений (n >30) в знаменателе обеих формулах берут n, а не n –1.
Следует заметить, что при определении средней арифметической (М) учитывают все элементы ряда, рассчитывая δ, надо брать не все случаи, а на единицу меньше (n–1), при n ≤30.
Рассчитаем среднее квадратическое отклонение, воспользовавшись условием задачи, приведенной в одном из предыдущих примеров.
Последовательность расчета δ (см. табл. 13):
1. Построить вариационный ряд (граф 1, 2).
2. Определить среднеарифметическую величину (М)
(графа 3):
дней
3. Найти истинные отклонения d (d = V – M). Например, d 1= 2–7= –5 и т.д., данные записать в графу 4.
4. Возвести каждое отклонение в квадрат (d 2), графа 5.
5. Найти произведение (d 2 P) по всем строкам ряда (графа 6).
6. Определить сумму Σ d 2 P, графа 6.
7. Рассчитать δ по формуле: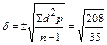 
=±2,4 дня.
Таблица 13
Распределение больных с острыми респираторными
заболеваниями по длительности нетрудоспособности (в днях)
| Алгоритм расчета среднего квадратического отклонения | |||||
| Длительность нетрудоспособности (в днях), V | Число больных р | Vр | d | d 2 | d 2 р |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 2 3 4 5 6 7 8 9 10 11 12 13 | 1 2 2 6 8 6 3 3 1 1 1 1 | 2 6 8 30 48 42 24 27 10 11 12 13 | -5 -4 -3 -2 -1 0 +1 +2 +3 +4 +5 +6 | 25 16 9 4 1 0 1 4 9 16 25 36 | 25 32 18 24 8 0 3 12 9 16 25 36 |
| Σр= n =35 | Σ Vр =233 | Σ d 2 p =208 | |||
По способу моментов среднее квадратическое отклонение определяется следующим образом:
,
где: a – условное отклонение вариант от условной средней (a = V – А).
Этот способ применяется тогда, когда вариационный ряд громоздкий как за счет большого числа наблюдений, так и за счет вариант, выраженных многозначными числами. При числе наблюдений, равном 30 и менее, в формуле n заменяют на (n – 1) и тогда δ определяется по формуле:
Если при расчете средней арифметической (М) была использована величина интервала (i), она вводится и в формулу расчета δ.
Разберем на том же примере статистическую обработку вариационного ряда с вычислением М и δ по способу моментов (табл. 14).
Таблица 14
Распределение больных с острыми респираторными
заболеваниями по длительности нетрудоспособности
| Длительность нетрудоспособности (в днях), V | Число больных, р | a | ар | а2 р |
| 1 | 2 | 3 | 4 | 5 |
| 2 3 4 5 А=6 7 8 9 10 11 12 13 | 1 2 2 6 8 6 3 3 1 1 1 1 | -4 -3 -2 -1 0 +1 +2 +3 +4 +5 +6 +7 | -4 -6 -4 -6 0 +6 +6 +9 +4 +5 +6 +7 | 16 18 8 6 0 6 12 18 16 25 36 49 |
| Σр= n =35 | Σ ар =23 | Σа2 р =210 |
Последовательность расчета δ по способу моментов:
1. Найти условную среднюю А (А =6).
2. Определить условные отклонения (a) каждой варианты (графа 3) от условной средней (a = V – А).
3. Получить произведения (ар), а затем их просуммировать (графа 4). В нашем примере Σ а р=23.
4. Рассчитать истинную среднюю арифметическую по формуле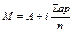 
. В нашем примере М =6,7 дней.
5. Получить произведения а2р по всем строкам вариационного ряда и просуммировать их (графа 5). В нашем примере Σ а2р =210.
6. Рассчитать δ по способу моментов по формуле: 
=2,4 дня.
Более упрощенный метод определения среднего квадратического отклонения – по амплитуде ряда, применяется, если отсутствуют необходимые данные для вычисления среднего квадратического отклонения обычным путем или нет необходимости в получении высокой точности показателя колеблемости вариационного ряда:
,
где: К – коэффициент, определяемый по таблице С.И. Ермолаева в зависимости от числа наблюдений (табл. 15).
Рассчитав этим способом среднее квадратическое отклонение для предыдущего примера, получим следующее значение δ:
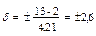дня.
Среднее квадратическое отклонение, вычисленное по амплитуде, может несколько отличаться от вычисленного обычным способом, причем различие это увеличивается с увеличением числа наблюдений. Так, δ, рассчитанная обычным способом, в нашем примере равна 2,4 дня, а по амплитуде – 2,6 дня.
Таблица 15
Значения коэффициента К для расчета среднего
квадратического отклонения по амплитуде вариационного ряда (таблица С.М. Ермолаева)
| n | Значения коэффициента К | |||||||||
| 0 | – | – | 1,13 | 1,69 | 2,06 | 2,33 | 2,53 | 2,70 | 2,85 | 2,97 |
| 10 | 3,08 | 3,17 | 3,26 | 3,34 | 3,41 | 3,47 | 3,53 | 3,59 | 3,64 | 3,69 |
| 20 | 3,73 | 3,78 | 3,82 | 3,86 | 3,90 | 3,93 | 3,96 | 4,00 | 4,03 | 4,06 |
| 30 | 4,09 | 4,11 | 4,14 | 4,16 | 4,19 | 4,21 | 4,24 | 4,26 | 4,28 | 4,30 |
| 40 | 4,32 | 4,34 | 4,36 | 4,38 | 4,40 | 4,42 | 4,43 | 4,45 | 4,47 | 4,48 |
| 50 | 4,50 | 4,51 | 4,53 | 4,54 | 4,56 | 4,57 | 4,59 | 4,60 | 4,61 | 4,63 |
| 60 | 4,64 | 4,65 | 4,66 | 4,68 | 4,69 | 4,70 | 4,71 | 4,72 | 4,73 | 4,74 |
| 70 | 4,75 | 4,77 | 4,78 | 4,79 | 4,80 | 4,81 | 4,82 | 4,83 | 4,83 | 4,84 |
| 80 | 4,85 | 4,86 | 4,87 | 4,88 | 4,89 | 4,90 | 4,91 | 4,91 | 4,92 | 4,93 |
| 90 | 4,94 | 4,95 | 4,96 | 4,96 | 4,97 | 4,98 | 4,99 | 4,99 | 5,00 | 5,01 |
Среднее квадратическое отклонение для относительной величины (Р) рассчитывается по формуле:
, где:
Р – величина относительного показателя, выраженного в % или ‰ и т.д.;
q – величина альтернативы (обратная величина Р), т.е. q =100 – Р или q =1000 – Р.
В статистической практике, прежде чем проводить соответствующую обработку и анализ результатов, полученных при конкретных наблюдениях, необходимо ясно представить себе, с каким законом распределения мы имеем дело. Вот почему одним из обязательных этапов методики статистической обработки вариационных рядов является графическое изображение вариационного ряда, которое позволяет определить, какому закону распределения подчиняется данное явление. Чаще всего встречается нормальное распределение, подчиняющееся закону Гаусса-Лапласа.
Для нормального распределения характерна симметричность, т.е. крайние варианты (наибольшие и наименьшие) встречаются редко. Чем ближе значения варьирующего признака к величине средней арифметической, тем чаще они встречаются.
Наиболее точным показателем, характеризующим симметричность распределения, является коэффициент асимметрии, который рассчитывается по формуле:
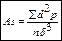
Коэффициент асимметрии – величина относительная, колеблется от 0 до 1. Если As равен 0, ряд симметричен, при As≤0,2 мы условно считаем ряд симметричным, а распределение нормальным.
Коэффициент асимметрии оценивается по специальной таблице (табл. 16).
Таблица 16
Критические значения коэффициента асимметрии As (Р+=0,95)
| n | As | n | As | n | As |
| 25 | 0,711 | 70 | 0,459 | 200 | 0,280 |
| 30 | 0,661 | 80 | 0,432 | 250 | 0,251 |
| 35 | 0,621 | 90 | 0,409 | 300 | 0,230 |
| 40 | 0,587 | 100 | 0,389 | 350 | 0,213 |
| 45 | 0,558 | 125 | 0,350 | 400 | 0,200 |
| 50 | 0,533 | 150 | 0,321 | 450 | 0,188 |
| 60 | 0,492 | 175 | 0,298 | 500 | 0,179 |
Если рассчитанный As≤As0,95 (табличного), отвергается предположение о наличии асимметрии, т.е. распределение можно считать нормальным. При As≥As0,95 распределение асимметрично. Знак As указывает направление асимметрии («–» – левосторонняя, «+» – правостороння). В этом случае применяется другая методика статистической обработки вариационных рядов.
Нормальное распределение имеет место, если изменчивость значений наблюдаемого явления обусловлена воздействием большого числа различных независимых факторов. Нормальное распределение представляет собой очень простой тип распределения, поскольку оно всегда принимает одну и ту же форму. Ее можно описать, выбрав в качестве меры колеблемости показатель среднеквадратического отклонения. При этом распределении максимальные и минимальные значения варьирующего признака практически не удаляются от среднего значения больше, чем на 3 δ, а весь вариационный ряд (его амплитуда) практически находится в пределах 6 δ.
Изобразим графически количественные характеристики нормального распределения (рис. 2).
Обращает на себя внимание, что на форму кривой существенное влияние оказывает среднее квадратическое отклонение. Чем больше δ, тем шире основание и ниже максимальная высота вариационной кривой (больше разнообразие варьирующего признака). Чем меньше значение δ, тем вариационная кривая уже и выше (совокупность более однородна). При этом площадь, ограничиваемая кривой и осью абсцисс, во всех случаях одинакова и условно может быть принята за единицу.
Если на оси абсцисс отложить вправо и влево от М величину 1 δ (М ± δ) и восстановить из этих точек перпендикуляры, то по теории вероятности (теория вероятности изучает законы поведения случайных величин) ограниченная площадь составит не менее 0,683 (68,3%) от всей площади, ограниченной вариационной кривой и осью абсцисс. Отсюда следует, что в пределах М ± δ находится не менее 68,3% всех вариант вариационного ряда (все варианты ряда находятся в пределах М ± δ с вероятностью безошибочного прогноза 68,3%).
Рис. 2 Нормальное распределение признака (М =12, δ =4)
По закону симметричности, отрезки М – δ и М + δ равны в вероятностном отношении и составляют не менее 34,1%. Аналогичным образом находим, что в пределах М ±2 δ находится не менее 95,5% всех вариант вариационного ряда, а в пределах М ±3 δ – 97,7%.
Таким образом, при нормальном распределении при различных значениях средней и среднеквадратического отклонения, всегда 68,3% наблюдений находятся в пределах ±1 δ; 95,5% наблюдений находятся в пределах ±2 δ; 99,7% – в пределах ±3 δ. И только 0,3% (3 случая на 1000) наблюдений имеют значения, отличные от среднего больше чем на 3 δ.
Среднее квадратическое отклонение имеет совершенно исключительное значение в статистике и используется в качестве абсолютной меры разнообразия, а также эта величина положена в основу почти всех характеристик изменчивости, распределения, корреляции, регрессии и дисперсионного анализа.
При помощи δ определяют типичность средней величины и меру ее точности. Если 95% всех вариант находятся в пределах М ±2 δ, то средняя является характерной для данного ряда, и не требуется увеличивать число наблюдений в выборочной совокупности.
В медицине с величиной М ± δ связано понятие нормы и патологии, отклонения от средней (в любую сторону) больше, чем на ± δ, но меньше, чем на ±2 δ, считается субнормальным (выше или ниже нормы). При отклонении от средней больше, чем на ±2 δ, варианты (показатели) считаются значительно отличающимися от нормы, т.е. патологическими.
Практическое значение среднего квадратического отклонения заключается в том, что зная М и δ, можно построить вариационные ряды.
Правило 3 δ применяется в народном хозяйстве при определении стандартов (для массового пошива одежды, обуви, производства мебели и т.д.). В медицинской статистике правило 3 δ применяется при изучении физического развития человека, оценке деятельности учреждений здравоохранения, комплексной оценке здоровья населения и т.д.
Среднее квадратическое отклонение является основной абсолютной мерой вариабельности варьирующих признаков, однако, при сравнении разнообразия двух или более совокупностей среднее квадратическое отклонение применяется при соблюдении двух условий:
1. Сравниваются только однородные совокупности (одноименные) или признаки.
2. Средние уровни сравниваемых признаков значительно отличаются друг от друга.
При несоблюдении этих условий δ не может быть использована для сравнения разнообразия и в этом случае в качестве относительной меры вариабельности применяется коэффициент вариации. Коэффициент вариации рассчитывается по формуле:
Коэффициент вариации в известной мере является критерием надежности средней арифметической. Если С V ≥40%, то средняя арифметическая неустойчива и ненадежна.
Оценка степени колеблемости изучаемых признаков по коэффициенту вариации может быть произведена по следующей схеме:
| С V (в %) | Степень колеблемости (рассеяние вариант около средней арифметической величины) |
| менее 10 | малая |
| от 10 до 20 | средняя |
| более 20 | сильная |
При нормальном распределении коэффициент вариации обычно не превышает 45 – 50% и часто бывает гораздо ниже этого уровня. В случаях же асимметричных распределений он может быть довольно высоким, достигающим 100% и выше.
Таким образом, обобщив материал по теме «Средние величины, их использование в здравоохранении» можно предложить алгоритмы статистической обработки медицинских данных с помощью средней величины (приложения 4-7).
