2020-10-11
97
симплекс-методом
Решить задачу, записанную в виде:
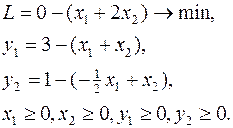
Составим симплексную таблицу:
| 
| 
| |
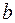
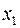
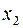
| L | 0 | 1 | 2 |
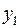
| 3 | 1 | 1 |
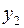
| 1 |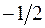 
| 1 |
Так как коэффициенты строки целевой функции неотрицательны, то начальное базисное решение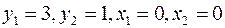 
не является оптимальным. Значение целевой функции для этого базиса L=0.
Выбираем ведущий столбец – это столбец, соответствующий переменной 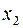. Выбираем ведущую строку. Для этого находим 
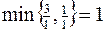. Следовательно, ведущая строка соответствует переменной .
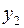Проводим преобразование симплексной таблицы, вводя переменную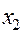 
в базис и выводя переменную 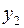из базиса. Получим таблицу:
|
|
|
| |
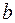
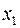
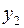
| L | -2 | 2 | -2 |
|
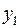
| 2 |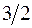 
| -1 |
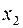
| 1 |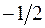
| 1 |
Одна итерация метода завершена. Переходим к новой итерации. Полученная таблица неоптимальная. Базисное решение, соответствующее таблице, имеет вид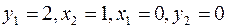 
. Значение целевой функции на этом базисе
L= -2.
Ведущий столбец здесь – столбец, соответствующий переменной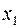 
. Ведущая строка – строка, соответствующая переменной 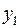. После проведения преобразований получим симплексную таблицу:
|
|
| 
| |
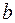
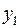
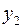
| L |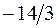 
| -4/3 | -2/3 |
|
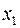
| 4/3 | 2/3 | -2/3 |
|
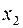
| 5/4 | 1/3 | 2/3 |
Еще одна итерация завершена. Переходим к новой итерации.
Строка целевой функции не содержит положительных значений, значит, соответствующее базисное решение
,
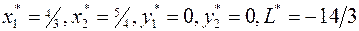является оптимальным и алгоритм завершает работу.
