Тема: Дерево игры. Поиск выигрышной стратегии.
Что нужно знать:
· в простых играх можно найти выигрышную стратегию, просто перебрав все возможные варианты ходов соперников
· для примера рассмотрим такую игру: сначала в кучке лежит 5 спичек; два игрока убирают спички по очереди, причем за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку
· первый игрок может убрать одну спичку (в этом случае их останется 4), или сразу 2 (останется 3), эти два варианта можно показать на схеме:

· если первый игрок оставил 4 спички, второй может своим ходом оставить 3 или 2; а если после первого хода осталось 3 спички, второй игрок может выиграть, взяв две спички и оставив одну:

· если осталось 3 или 2 спички, то 1-ый игрок (в обеих ситуациях) выиграет своим ходом:

· простроенная схема называется «деревом игры», она показывает все возможные варианты, начиная с некоторого начального положения (для того, чтобы не загромождать схему, мы не рисовали другие варианты, если из какого-то положения есть выигрышный ход)
· в любой ситуации у игрока есть два возможных хода, поэтому от каждого узла этого дерева отходят две «ветки», такое дерево называется двоичным (если из каждого положения есть три варианта продолжения, дерево будет троичным)
· проанализируем эту схему; если первый игрок своим первым ходом взял две спички, то второй сразу выигрывает; если же он взял одну спичку, то своим вторым ходом он может выиграть, независимо от хода второго игрока
· кто же выиграет при правильной игре? для этого нужно ответить на вопросы: 1) «Может ли первый игрок выиграть, независимо от действий второго?», и 2) «Может ли второй игрок выиграть, независимо от действий первого?»
· ответ на первый вопрос – «да»; действительно, убрав всего одну спичку первым ходом, 1-ый игрок всегда может выиграть на следующем ходу
· ответ на второй вопрос – «нет», потому что если первый игрок сначала убрал одну спичку, второй всегда проиграет, если первый не ошибется
· таким образом, при правильной игре выиграет первый игрок; для этого ему достаточно первым ходом убрать всего одну спичку
· в некоторых играх, например, в рэндзю (крестики-нолики на бесконечном поле) нет выигрышной стратегии, то есть, при абсолютно правильной игре обоих противников игра бесконечна (или заканчивается ничьей); кто-то может выиграть только тогда, когда его соперник по невнимательности сделает ошибку
· полный перебор вариантов реально выполнить только для очень простых игр; например, в шахматах сделать это за приемлемое время не удается (дерево игры очень сильно разветвляется, порождая огромное количество вариантов)
· все позиции в простых играх делятся на выигрышные и проигрышные
· выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку; при этом говорят, что у него есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть
· если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник; в этом случае говорят, что у него нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника
· выигрышные и проигрышные позиции можно охарактеризовать так:
- позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная;
- позиция, из которой хотя бы один из возможных ходов ведет в проигрышную позицию - выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.
Пример задания:
P-09. (Демо-вариант 2018 года, проект)Два игрока, Петя и Ваня играют в следующую игру. На столе в кучке лежат фишки. На лицевой стороне каждой фишки написано двузначное натуральное число, обе цифры которого находятся в диапазоне от 1 до 4. Никакие две фишки не повторяются. Игра состоит в том, что игроки
поочередно берут из кучки по одной фишке и выкладывают в цепочку на стол лицевой стороной вверх таким образом, что каждая новая фишка ставится правее предыдущей и ближайшие цифры соседних фишек совпадают. Верхняя часть всех выложенных фишек направлена в одну
сторону, то есть переворачивать фишки нельзя. Например, из фишки, на которой написано 23, нельзя сделать фишку, на которой написано 32. Первый ход делает Петя, выкладывая на стол любую фишку из кучки. Игра заканчивается, когда в кучке нет ни одной фишки, которую можно добавить в цепочку. Тот, кто добавил в цепочку последнюю фишку, выигрывает, а его противник проигрывает. Будем называть партией любую допустимую правилами последовательность ходов игроков, приводящую к завершению игры. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит указать, какую фишку он должен выставить в любой ситуации, которая ему может встретиться при различной игре противника.
Пример. Пусть на столе в кучке лежат фишки: 11, 12, 13, 21, 22, 23
Пусть первый ход Пети 12. Ваня может поставить 21, 22 или 23. Предположим, он ставит 21. Получим цепочку 12-21. Петя может поставить 11 или 13. Предположим, он ставит 11. Получим цепочку 12-21-11. Ваня может поставить только фишку со значением 13. Получим цепочку 12-21-11-13. Перед Петей в кучке остались только фишки 22 и 23, то есть нет фишек, которые он мог бы добавить в цепочку. Таким образом, партия закончена, Ваня выиграл.
Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
Задание 1.
а) Приведите пример самой короткой партии, возможной при данном наборе фишек. Если таких партий несколько, достаточно привести одну.
б) Пусть Петя первым ходом пошел 42. У кого из игроков есть выигрышная стратегия в этой ситуации? Укажите первый ход, который должен сделать выигрывающий игрок, играющий по этой стратегии. Приведите пример одной из партий, возможных при реализации выигрывающим игроком этой стратегии.
Задание 2
Пусть Петя первым ходом пошел 44. У кого из игроков есть выигрышная стратегия, позволяющая в этой ситуации выиграть своим четвертым ходом? Постройте в виде рисунка или таблицы дерево всех партий, возможных при реализации выигрывающим игроком этой стратегии. На рёбрах дерева указывайте ход, в узлах – цепочку фишек, получившуюся после этого хода.
Задание 3
Укажите хотя бы один способ убрать 2 фишки из исходного набора так, чтобы всегда выигрывал не тот игрок, который имеет выигрышную стратегию в задании 2. Приведите пример партии для набора из 6 оставшихся фишек.
Задание 1а.
1) партия заканчивается, когда цепочка закончилась на цифре X и не осталось ни одной фишки, которая бы начиналась с этой цифры;
2) меньше всего фишек заданного набора начинается с цифры 1 (только 12 и 14), поэтому самой короткой партией, вероятно, будет партия, которая заканчивается на цифре 1 (фишкой 21 или 41), при этом фишки 12 и 14 должны быть выставлены;
3) соединить эти фишки в цепочку можно с помощью фишек 21 или 41, таким образом, получается две возможных самых коротких партии:
12 – 21 – 14 – 41 и 14 – 41 – 12 – 21.
В ответе достаточно привести одну из них.
Задание 1б. (Идея решения – А. Сидоров).
4) заметим, что эта игра напоминает «одностороннее домино», в котором фишки можно выставлять только одной стороной и наращивать цепочку можно тоже только с одной стороны;
5) среди фишек есть две особые – 22 и 44 («дубли») они служат для того, чтобы передать ход сопернику; если выставить дубль, оказавшись в проигрышной позиции, то эта проигрышная позиция «переходит» к сопернику
6) пока построим дерево без учёта дублей, то есть для набора фишек
12, 14, 21, 24, 41 и 42
7) по условию Петя выставляет первым ходом фишку 42, дальнейшие варианты развития игры показаны на схеме:

8) итак, мы видим, что если никто из игроков не выставляет дублей, то выигрывает Ваня во всех случаях, причем все партии заканчиваются на цифре 4
9) если Ваня в ходе игры не выставит дубль, то в конце каждой ветки Петя может выставить дубль 44 и выиграть:

10) поэтому теперь посмотрим, где Ваня может изменить игру дублями; Ване нет смысла ставить дубль 44, потому что во всех вариантах партий он уже есть (с выигрышем для Пети), так что выставление дубля 44 просто перемещает его в середину цепочки, не изменяя её длину
11) у Вани в распоряжении есть еще дубль 22; на следующем рисунке выделены ходы, где Ваня может поставить этот дубль:
|

12) использование дубля 22 действительно изменяет игру, так как удлиняет цепочки на 1, при этом выигрывает Ваня:
а) Ваня может своим первым ходом выставить дубль 22, при этом он всегда выиграет
б) Ваня может первым ходом выставить фишку 21, при этом получив ход в позиции, когда текущая цепочка заканчивается на 2, он выставляет дубль 22 и выигрывает
Задание 2.
13) построим дерево игры для случая, когда Петя в самом начале ходит фишкой 44, «забыв» пока про дубль 22:

14) по дереву видим, что при игре без дубля 22 выигрывает Петя своим третьим или четвёртым ходом
15) Ваня может изменить ход игры дублем 22 только в выделенных узлах, поэтому
· если Ваня походит фишкой 41, Петя должен ответить ходом 14
· если Ваня походит фишкой 42, Петя должен ответить ходом 21
16) при записи неполного дерева игры, доказывающего выигрыш Пети, нужно учесть, что по условию задачи нужно представить дерево с выигрышем именно в 4 хода, хотя Петя имеет стратегию выигрыша за 3 хода:

Задание 3.
17) в задании 2 выигрывает Петя, поэтому нужно убрать две фишки таким образом, чтобы всегда выигрывал Ваня
18) заметим, что нам нужно доказать, что Ваня выигрывает ВСЕГДА, при любом первом ходе Пети; это значит, что построение одного дерева (при конкретном первом ходе) ничего не доказывает
19) заметим, что последней цифрой цепочки для данного набора фишек всегда будет 1, 2 или 4, поэтому можно построить такой граф возможных переходов (например, ребро перехода 1 ® 2 соответствует фишке 12, а петля у узла 2 – фишке 22):

по каждому ребру этого графа можно пройти только один раз (каждая фишка выставляется один раз)
20) по этому графу видно, что если убрать две петли, остается граф с одинаковой ситуацией для каждой из вершин: есть два контура, проходящие в разных направлениях через все узлы
21) итак, если убрать два дубля, то всегда будут выставлены 4 или все 6 фишек, поскольку 4 и 6 – чётные числа, то всегда выиграет Ваня, потому что он делает все ходы с чётными номерами; например, при первом ходе Пети 12 возможны партии:
12 – 21 – 14 – 41 или 12 – 24 – 41 – 14 – 42 – 21.
Ещё пример задания:
P-08. Два игрока, Петя и Ваня играют в следующую игру. Задан некоторый набор символьных цепочек («слов»), в котором ни одно слово не является началом другого (выполняется условие Фано). Игра начинается с пустой строки, в конец которой игроки по очереди дописывают буквы, по одной букве за ход так, чтобы полученная цепочка на каждом шаге была началом одного из заданных слов. Первый ход делает Петя. Выигрывает тот, кто первый составит слово из заданного набора.
Пример. Пусть заданы слова {МАК, МЫЛО, РАМА, РАК}. На первом ходу Петя может написать букву М или Р. Пусть он написал букву М. В ответ Ваня может написать А или Ы. В первом случае получается МА, и Петя, дописав букву К, получает слово МАК из заданного набора и выигрывает. Во втором случае получается МЫ, Петя вынужден дописать Л и Ваня выиграет вторым ходом, дописав О и получив слово МЫЛО.
Задание 1.
а) Определите, у кого из игроков есть выигрышная стратегия для набора слов {ВАРЕНЬЕ, КОРОВА}. Опишите эту стратегию. Определите, сколько различных партий может быть сыграно при этой стратегии и какое слово будет получено в каждом случае.
б) Определите, у кого из игроков есть выигрышная стратегия для набора слов {НУБНУБ…НУБ, PUMAPUMA…PUMA}. В первом слове 55 раз повторяется слово НУБ, а во втором – 32 раза повторяется слово PUMA. Опишите эту стратегию. Определите, сколько различных партий может быть сыграно при этой стратегии и какое слово будет получено в каждом случае.
Задание 2
В наборе слов, приведённом в задании 1а, поменяйте местами две буквы в любом слове так, чтобы выигрышная стратегия была у другого игрока. Опишите эту стратегию. Определите, сколько различных партий может быть сыграно при этой стратегии и какое слово будет получено в каждом случае.
Задание 3
Дан набор слов {МОРОКА, МОРС, МОРОЗ, ПЛАХА, ПЛАТЬЕ, ПЛОМБА}. У кого из игроков есть выигрышная стратегия? Приведите в виде рисунка или таблицы дерево всех партий, возможных при этой стратегии.
1) Сначала предположим, что в наборе одно слово. Если игроки дописывают каждый раз по одной букве то очевидно, что первый из них (Петя) допишет все нечётные буквы, а второй (Ваня) – все чётные. Таким образом, если в слове нечётное число букв, выиграет Петя, а если чётное – Ваня.
2) Если слов несколько, то стратегия Пети состоит в том, чтобы все время выбирать такое продолжение, при котором в итоге будет получено слово с нечётным количеством букв, а Ваня наоборот должен пытаться перескочить на слово с чётным количеством букв.
3) Задание 1а. В слове ВАРЕНЬЕ – 7 букв (нечётное количество, выиграет Петя), а в слове КОРОВА – 6 букв (чётное количество, выиграет Ваня). Петя ходит первый и может написать букву В. Поскольку слово КОРОВА начинается с другой буквы, Ваня будет вынужден «идти» по слову ВАРЕНЬЕ и проиграет. Этот вариант – единственный, то есть возможна только одна партия, при которой Петя следует своей стратегии, она заканчивается словом ВАРЕНЬЕ.
Задание 1а.
- Для набора слов {ВАРЕНЬЕ, КОРОВА} выигрышная стратегия есть у Пети.
- Выигрышная стратегия Пети состоит в том, чтобы написать первую букву В. Далее остается только одно допустимое слово – ВАРЕНЬЕ, и Петя выиграет, так как в этом слове 7 букв и он допишет последнюю букву, имеющую нечётный номер.
- При выбранной стратегии возможна только одна партия.
- В результате этой партии получится слово ВАРЕНЬЕ.
4) Задание 1б. В первом слове набора 3*55 = 165 букв, нечётное количество. Поэтому если игра «пойдёт» по первому слову, то выиграет Петя. Во втором слове 4*32 = 128 букв, чётное количество. Поэтому если игра пойдёт по второму слову, выиграет Ваня. Слова начинаются с разных букв, поэтому Петя может выбрать, по какому слову пойдёт игра. Если он напишет букву Н, он выиграет.
Задание 1б.
- Для заданного набора слов выигрышная стратегия есть у Пети.
- Выигрышная стратегия Пети состоит в том, чтобы написать первую букву Н. Далее остается только одно допустимое слово – НУБНУБ…НУБ, и Петя выиграет, так как в этом слове нечётное количество букв (165) и он допишет последнюю букву, имеющую нечётный номер.
- При выбранной стратегии возможна только одна партия.
- В результате этой партии получится слово НУБНУБ…НУБ.
5) Задание 2. В наборе слов {ВАРЕНЬЕ, КОРОВА} первое слово имеет нечётное количество букв, а второе – чётное. Чтобы Ваня мог выиграть, он должен получить возможность «перескочить» на второе слово. Для этого при любом ходе Пети у Вани должен остаться выбор. Это возможно только в том случае, когда оба слова начинаются с одной и той же буквы. Поскольку разрешается переставлять буквы только в одном слове, мы не можем сделать, чтобы оба слова начинались с буквы К – в первом слове её нет. Но можно сделать так, чтобы оба слова начинались с буквы В, переставив буквы К и В в слове КОРОВА. Получается набор {ВАРЕНЬЕ, ВОРОКА}, и Ваня выигрывает, своим первым ходом дописав букву О к букве В, которую (обязательно!) напишет Петя.
Задание 2.
- Для того, чтобы Ваня мог выиграть, во втором слове нужно поменять местами буквы К и В.
- Так как оба слова начинаются с буквы В, Петя обязательно напишет букву В. Выигрышная стратегия Вани состоит в том, чтобы своим ходом дописать букву О. После этого игра «идёт» по слову ВОРОКА, в нём чётное количество букв и выигрывает Ваня, который допишет последнюю букву.
- При выбранной стратегии возможна только одна партия.
- В результате этой партии будет получено слово ВОРОКА.
6) Задание 3. Расположим слова в столбики по начальным буквам, на каждом шаге вниз стараясь сохранить наибольшую общую часть (маркером выделена часть слова, которая совпадает с предыдущим словом в том же столбике):
МОРОКА + ПЛАХА
+ МОРОЗ ПЛАТЬЕ
МОРС ПЛОМБА
Знаком «плюс» отмечены слова, имеющие нечётное количество букв – это выигрышные варианты для Пети.
7) Если Петя первой напишет букву М, для выигрыша ему нужно перейти на слово МОРОЗ, но как только он составит слово МОР, Ваня тут же допишет С и выиграет, получив слово МОРС.
8) Если Петя напишет букву П, Ваня вынужден написать Л (это вторая буква всех оставшихся допустимых слов). Теперь Петя может написать А или О. В обоих случаях Ваня может перевести игру на слова с чётным количество букв (ПЛАТЬЕ, ПЛОМБА) и выиграть. Таким образом, при этом наборе слов выигрышную стратегию имеет Ваня.
Задание 3.
- Для набора слов {МОРОКА, МОРС, МОРОЗ, ПЛАХА, ПЛАТЬЕ, ПЛОМБА} выигрышная стратегия есть у Вани.
- Дерево всех возможных партий приводится на рисунке. Для Пети мы рассматриваем все возможные ходы, для Вани – только выигрышный вариант на каждом шаге. Буквами над схемой обозначены игроки (П – ход Пети, В – ход Вани).

Вместо рисунка можно использовать таблицу (зелёным цветом отмечен выигрыш Вани):
| Начальная позиция | П | В | П | В | П | В |
| – | М | МО | МОР | МОРС | ||
| П | ПЛ | ПЛА | ПЛАТ | ПЛАТЬ | ПЛАТЬЕ | |
| ПЛО | ПЛОМ | ПЛОМБ | ПЛОМБА |
Ещё пример задания:
P-07. Два игрока, Петя и Ваня играют в игру с цепочками символов. Игра начинается со слова, которое состоит из n букв Ю и m букв Я. Такое слово будем обозначать как (n, m). Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
1) добавить в слово одну букву, Ю или Я
2) удвоить количество букв Ю
3) удвоить количество букв Я
Игра завершается в тот момент, когда длина слова становится не менее 65 символов. Победителем считается игрок, сделавший последний ход, т.е. первым получивший слово длиной 65 или больше.
Задание 1
Для каждой из начальных позиций (6, 29), (8, 28) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 2
Для каждой из начальных позиций (6, 28), (7, 28), (8, 27) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 3
Для начальной позиции (5, 28) укажите, кто из игроков имеет выигрышную стратегию. Опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. Постройте дерево всех партий, возможных при указанной Вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.
1) По сути, это та же самая задача с двумя камнями, в которой буквы Ю – это первая куча камней, а буквы Я – вторая.
2) Задание 1. Рассмотрим все возможные ходы из позиции (6, 29). Если среди них найдётся хотя бы одна проигрышная, то эта позиция будет выигрышной. Итак:
(6, 29) ® (7,29) ® (7,58)
® (6,30) ® (6,60)
® (12,29) ® (12,58)
® (6,58) ® (6,116)
Все ходы ведут в выигрышные позиции, из которых второй первым же ходом выигрывает (эти позиции выделены жёлтым маркером). Поэтому позиция (6, 29) – проигрышная. Аналогично рассматриваем все ходы из позиции (8, 28):
(8, 28) ® (9,28) ® (9,56)
® (8,29) ® (8,58)
® (16,28) ® (16,56)
® (8,56) ® (8,112)
Эта позиция тоже проигрышная.
Задание 1. В каждой из начальных позиций (6, 29), (8, 28) выигрышную стратегию имеет Ваня. При любом ходе Пети ему нужно удвоить количество букв Я. Во всех случаях он выигрывает своим первым ходом, так как в результате его хода получается слово длиной не менее 65 символов.
3) Задание 2. В каждой из начальных позиций (6, 28), (7, 28), (8, 27) выигрышную стратегию имеет Петя. Своим первым ходом ему нужно перевести игру в позицию (6, 29) в первом случае или (8, 28) во втором и третьем случаях. Выше было доказано, что это позиции проигрышные для Вани.
4) Задание 3. Теперь рассмотрим позицию (5, 28). Из этой позиции есть ходы в позиции
(6, 28), (5, 29), (10, 28) и (5, 56). Сразу видим, что позиции (10, 28) и (5, 56) – выигрышные, потому что в каждой из них удвоение второго значения даёт сумму больше 65. Позиция (6, 28), как мы доказали ранее, тоже выигрышная. Осталось разобраться с позицией (5, 29). Из неё есть ход в проигрышную позицию (6, 29) – см. результат выполнения задания 1, поэтому это выигрышная позиция. Таким образом, все ходы из позиции (5, 28) ведут в выигрышные позиции, то есть эта позиция проигрышная, и при правильной игре выиграет Ваня.
5) Остается нарисовать неполное дерево игры. Для выигрывающего игрока на каждом ходу выбираем только один вариант, который ведёт к выигрышу, а для проигрывающего (Пети) рассматриваем все возможные ходы, чтобы доказать, что ему не уйти от проигрыша:
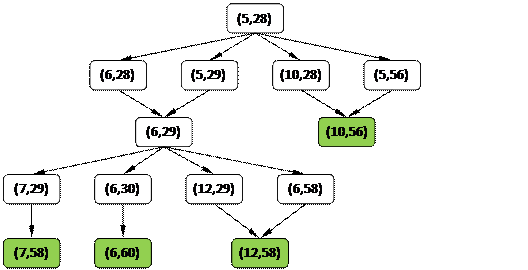
То же решение в виде таблицы
| Начало | Петя | Ваня | Петя | Ваня |
| (5,28) | (6,28) | (6,29) | (7,29) | (7,58) |
| (6,30) | (6,60) | |||
| (5,29) | (12,29) | (12,58) | ||
| (6,58) | ||||
| (10,28) | (10,56) | |||
| (5,56) | ||||
6) Задание 3. Из позиции (5, 28) все возможные ходы ведут в выигрышные позиции (6,28), (5,29), (10,28) и (5,56), поэтому эта позиция проигрышная, и при правильной игре выиграет Ваня. Последовательность ходов, которая приводит к победе при любых ходах Пети, показана на рисунке.
 2020-10-10
2020-10-10 878
878







