Пространственная система сил. Понятие динамического винта

Пространственная система сил

2.6. Пространственная система сил Система сил называется пространственной, если линии их действия расположены в пространстве произвольным образом. Для пространственных систем сил остаются справедливыми все те положения, которые были сформулированы для плоской системы сил. Так, равнодействующая сходящихся сил в трехмерном случае Условие уравновешенности пространственной системы сходящихся сил может быть сформулировано в одной из трех форм: в векторной форме: в графической форме: силовой многоугольник должен быть замкнут. в аналитической форме: сумма проекций всех сил на каждую из осей декартовой системы координат должна быть равна нулю Момент силы относительно точки в трехмерном случае определяется несколько сложнее. Именно, момент МС(F) силы F относительно некоторой точки С равен векторному произведению радиус-вектора r, проведенного из точки С в точку приложения силы, на силу F: МС(F) = r х F. (2.10) В соответствии с правилами векторного произведения момент МС(F) представляет собой вектор, перпендикулярный плоскости, в которой лежат вектора r и F, и направленный так, что сила стремится повернуть тело против часовой стрелки, если смотреть со стороны вектора МС(F). Модуль момента силы равен: где h = r sin - расстояние от точки С до линии действия силы F,? - угол между радиус-вектором и силой (рис. 12). Оно, как и в плоском случае, называется плечом силы. Плечо силы не изменится, если точка приложения силы будет перемещаться вдоль линии ее действия. Поэтому величина момента МС(F) не зависит от того, где выбрана точка приложения силы. Из формулы (2.11) видно, что момент силы относительно точки равен нулю в двух случаях: либо, когда сила равна нулю, либо, когда точка С лежит на линии действия силы. Теорема Вариньона для пространственной системы сил имеет более общую форму, чем соотношение (2.5) для плоской системы сил: если произвольная пространственная система сил имеет равнодействующую, то момент равнодействующей относительно некоторой точки равен векторной сумме моментов всех сил системы относительно той же точки. Как известно из аналитической геометрии, векторное произведение (2.10) может быть записано через определитель где i, j, k – орты декартовой системы координат с центром в точке С; x, y, z – проекции радиус-вектора; Fx, Fy, Fz – проекции силы на соответствующие координатные оси. Равенство (2.12) можно рассматривать как разложение вектора МС(F) по осям координат. Следовательно, каждый сомножитель перед единичным ортом представляет собой проекцию вектора МС(F) на соответствующую ось. Моментом Мm(F) силы F относительно некоторой оси m называется скалярная величина, равная проекции на ось m момента силы F относительно какой-либо точки, взятой на этой оси. Для вычисления момента силы относительно оси удобно воспользоваться следующим несложным построением: сначала провести плоскость перпендикулярную оси m и найти точку их пересечения, затем спроектировать силу на эту плоскость. Момент проекции относительно точки пересечения и будет равен моменту силы F относительно оси m. Правило знака для момента Мm(F) такое же как и при вычислении момента силы относительно точки. Момент силы относительно оси равен нулю тогда, когда сила F лежит в одной плоскости с осью m. В самом деле, в этом случае либо проекция силы на плоскость, перпендикулярную оси, равна нулю (сила F параллельна оси m), либо линия действия проекции силы проходит через точку пересечения указанной плоскости и оси. Из определения момента силы относительно оси следует, что сомножители перед единичными ортами в формуле (2.12) равны моментам силы F относительно осей декартовых координат: Мх(F) = yFz – zFy; My(F) = zFx – xFz; Mz(F) = xFy – yFx. Эти формулы позволяют вычислить моменты силы относительно координатных осей, если известны координаты точки приложения силы и ее проекции на оси координат. Пара сил для трехмерного случая определяется также как и для плоского случая. Однако, плоскость действия пары и, следовательно, вектор ее момента могут быть ориентированы в пространстве произвольным образом. Отсюда следует, что две пары сил будут эквивалентны, если векторы их моментов равны друг другу. Следовательно, пару сил можно переносить в пространстве произвольным образом, оставляя плоскость ее действия параллельной самой себе. Если к телу приложены несколько пар сил с моментами М1, М2, …, М n, то момент равнодействующей пары равен векторной сумме моментов всех пар: n

Часные случаи приведения пространственной системы сил к простейшему виду

Случаи приведения к простейшему виду

Приведение к паре

Пусть в результате приведения сил к центру О оказалось, что главный вектор равен нулю, а главный момент отличен от нуля: . Тогда в силу основной теоремы статики можем написать

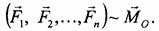
Это означает, что исходная система сил в этом случае эквивалентна паре сил с моментом .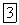

Момент пары не зависит от того, какая точка выбрана в качестве центра моментов при вычислении момента пары. Следовательно, в данном случае главный момент не должен зависеть от выбора центра приведения. Но именно к этому выводу и приводит соотношение

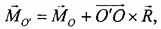
связывающее главные моменты относительно двух различных центров. При добавочный член также равен нулю, и мы получаем

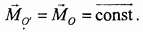
 Приведение пространственной системы сил к простейшему виду

Докажем вначале лемму: Не изменяя действия силы на твердое тело, ее можно перенести с линии действия, параллельно самой себе, добавляя при этом пару моментом, равным моменту исходной силы относительно новой точки приложения силы.

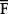Рассмотрим силу , приложенную в точке А. Выберем произвольно точку В, ней приложим две силы, 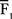и 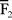, так, что модули всех трех сил равны и они параллельны.

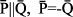
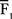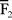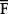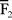Очевидно силы и образуют уравновешенную систему, поэтому можно добавить их системе. Силы и образуют пару сил, итоге получаем силу 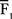пару сил .

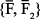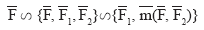
Рассмотрим произвольную систему сил.

Система состоит из сил 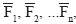, приложенных в точках 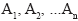. Выберем точку О, дальнейшем будем называть ее центром приведения системы сил, и перенесем последовательно эту точку все силы системы, добавляя всякий раз пару c моментом, равным моменту исходной силы относительно новой точки приложения силы. После переноса силы обозначение добавляем «'», чтобы отличать исходную силу от той же силы новом положении, пару силы 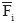обозначаем 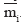. Силы, приложенные точке О, можно сложить получим силу 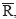Вектор-моменты пар тоже можно сложить получим одну пару, равную сумме моментов всех исходных сил относительно центра О.

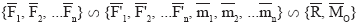
Здесь введены обозначения:
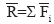– главный вектор системы сил;
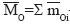– главный момент системы сил относительно центра О.
Очевидно что главный вектор системы сил не зависит от положения центра приведения, главный момент системы очевидно меняется при изменении центра приведения. Заметим, что проекция главного момента
на направление главного вектора системы тоже не зависит от положения центра приведения, но доказывать это не будем.