Решение треугольника

Обратная геодезическая задача

Прямая геодезическая задача

Прямой геодезической задачей называется способ определения координат какой-либо точки по известным координатам другой точки, дирекционному углу и расстоянию между ними.

Пусть точка A (рисунок 30) имеет координаты х₁и у₁. Из точки А на точку В определен дирекционный угол α_1,2 и между точками измерено расстояние S.

Необходимо найти координаты х₂ и у₂ точки В.

Решение. Проведем через точки А и В линии, параллельные осям координат. Из образовавшихся построений искомые координаты точки выразятся:

х₂= х₁ + АС;

у_{2 =}у₁+ СВ.

Следовательно, решение прямой задачи сводится к отысканию значений отрезков АС и СВ.

Отрезки АС и СВ являются катетами прямоугольного треугольника ABC и равны проекциям линии АВ на оси координат.

Проекции горизонтальных проложений линии S на оси X и Y называются приращениями координат и обозначаются соответственно AС = Δх и ВС=Δу.

Приращения координат Δх и Δу могут быть положительными и отрицательными. Знак приращения определяется значением дирекционного угла линии АВ.

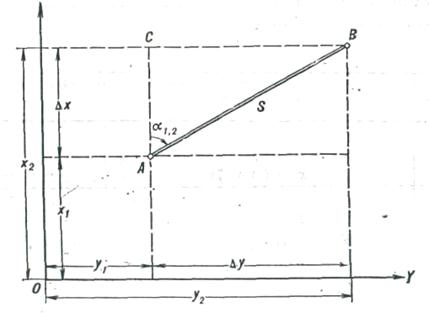
Рисунок 30 – Прямая (обратная) геодезическая задача

Пример. Приращения координат точки В относительно точки А будут положительными (I четверть). Приращения координат точки A относительно точки В будут отрицательными (III четверть).

Значения приращений координат находят из соотношений прямоугольного треугольника ABC:

Δх = S·cos α_{1, 2}; Δу = S·sin α_{1, 2} (8)

отсюда значения координат точки Вбудут:

х₂ = х₁ + Δх = х₁ + S·Cos α_{1, 2}; у₁ + Δу = у₁ + S·Sin α_{1, 2}.

х₂ = х₁ + Δх = х₁ + S cos α_{1, 2}; (9)

у₁ + Δу = у₁ + S sin α_{1, 2}.

Практическое решение прямой геодезической задачи производится на вычислительных машинах с использованием таблиц натуральных значений тригонометрических функций.

Вычисления выполняют в следующим порядке (таблица 6).

Таблица 6 – Порядок решения прямой геодезической задачи

№ действия	Элементы формул	Величина
	α_{1, 2} х₂ = (1) + (7)	200^о48'00" 6^о106^о845,1

Продолжение таблицы – 6

№ действия	Элементы формул	Величина
	х₁ Δх = (3)·(6) Cos α_{1, 2} S Sin α_{1, 2} Δу = (3) · (5) y₁ y₂ = (2) + (8) s_конр =	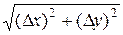6^о115 105,3 - 8 260,2 - 0,934 826 8 836,1 - 0,55 107 - 3 137,8 7 534 664,7 7 531 526,9 8 836,1

- выписывают значения исходных данных х₁, y₁, S и α_{1, 2} (действия 1 ‑ 4);

- вычисляют приращения координат Δх и Δу (действия 5 – 8);

- вычисляют координаты х₂, y₂ точки В (действия 9 и. 10);

- проводят контроль вычислений путем определения значения s_конр по формуле

S_конр= .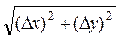

Расхождение S и S_конр более чем на единицу последнего знака свидетельствует о наличии ошибок, которые выявляют повторной проверкой всех вычислений.

Обратной геодезической задачей называется способ определения дирекционного угла и расстояния между двумя точками по известным их координатам.

Возвратимся к рисунку 30. Из условия обратной задачи известны: прямоугольные координаты точек А и В (х₁и y₁; х₂ и y₂).

Необходимо найти расстояние s между точками А и В и дирекционный угол α_{1, 2}из точки А на точку В.

Решение. Искомые величины находят из соотношений прямоугольного треугольника ABC:

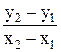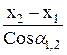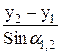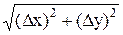tg α_{1, 2} =; s= = =. (10)

По значению тангенса с помощью тригонометрических таблиц определяют величину только острого угла. Острый угол, отсчитываемый от ближайшего направления оси абсцисс (северного или южного) до направления данной линии, называется румбом и обозначается буквой r.

Для отыскания значения дирекционного угла по значению румба определяют четверть, в которой находится искомое направление.

Четверть, в которой находится направление АВ, определяют по знакам приращений координат Δх и Δу, вычисляемых как разности абсцисс и ординат:

Δх = x₂– x₁; Δу = y₂ – у₁[4].

Формулы перехода от румба к дирекционному углу в зависимости от знака приращения координат приведены в таблице 7.

Таблица 7 – Переход от румба к дирекционному углу

Четверть круга	Знак приращения	Формулы перехода от румба к дирекционному углу
Δх	Δу
I II III IV	+ – – +	+ + – –	α = r α = 180^o – r α = 180^o + r α = 360^o – r

Искомое расстояние S определяют по формулам (10).

Наличие двух вариантов формул обеспечивает надежный контроль вычисления расстояния.

Вычисление расстояний и дирекционных углов при решении обратной геодезической задачи производят с использованием вычислительных машин и таблиц натуральных значений тригонометрических функций в следующем порядке, таблица 8:

Таблица 8 – Решение обратной геодезической задачи.

№ действия	Элементы формул	Величина

	y₂ у₁. Δу = (4) – (2) x₂ x₁ Δх = (3) – (1) tg α_{1, 2} = (6): (5) r	7 579 739,3 7 580 202,1 - 462,8 6 406 199,0 6 411 279,2 - 5 080,2 0,091 099 5о 12'19"

Продолжение таблицы 8

№ действия	Элементы формул	Величина

	α_{1, 2} Sin α_{1, 2} Cos α_{1, 2} S₁ S₂ S_ср	185^о 12'19" 0,090 724 0,995 786 5 101,2 5 101,2 50 101,2

- выписывают координаты исходных пунктов. х₁, y₁, х₂, у₂(действия 1 ‑ 4);

- вычисляют приращения координат Δх и Δу (действия 5 и 6); при этом всегда из координат второй точки алгебраически вычитают координаты первой точки;

- вычисляют тангенс дирекционного угла (действие 7);

- по тангенсу угла находят румб, который затем переводят в дирекционный угол с помощью таблицы 7, выбирают из таблиц синус и косинус этого угла (действия 8 – 11);

- дважды вычисляют расстояние s и за окончательное значение берут среднее из обоих результатов, при этом расхождение S₁ – S₂ не должно превышать более двух единиц последнего знака (действия 12 – 14).

Решением треугольника называется определение всех его сторон и углов по трем известным элементам, из которых хотя бы один должен быть его стороной.

Решение треугольника осуществляют по формулам соотношений его элементов, известных из курса тригонометрии.

Обозначив в треугольнике AВС (рисунок 31) стороны через а, в и с, а углы через А, В и С, запишем основные соотношения:

А + В + С = 180° (теорема суммы углов);

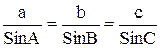(теорема синусов);

а² = в² + с² – 2·в·сcos A (теорема косинусов);

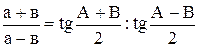(теорема тангенсов)

и дополнительные соотношения:

Sin A = Sin· (B + C);

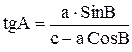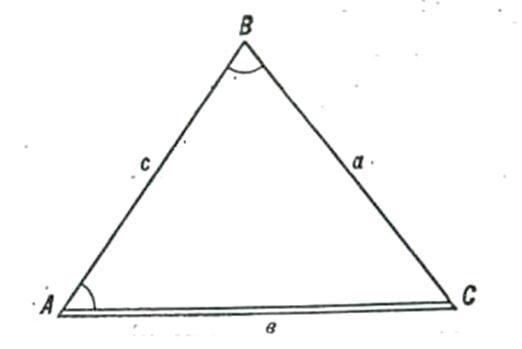
Рисунок 31 – Треугольник

Пример. Пусть в треугольнике ABC (рисунок 31) известны сторона в и углы А и В. Необходимо найти угол С и стороны а и с.

Решение проводят в следующем порядке:

- угол С находят по теореме суммы углов

- С = 180^о – (А + В);

- стороны а и с вычисляют по теореме синусов

; ;

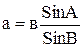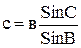- контроль вычислений осуществляют по формуле

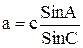Пример вычислений приведен в таблице 9.

Таблица 9 – Решение треугольника

№ действия	Элемент формулы	Величина
	А	86^о15'43"
	В С = [180^o – (1) + (2)] Контроль: (1) + (2) +(4) = 180^о	46^о34'52" 47^о09'25" 180^о00'00"
	Sin A Sin B Sin C	0,997 873 0,726 348 0,733 220
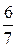	а = (3) в с = (3) 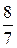Контроль: а_контр = (10)	6^о448,3 4^о693,7 4^о738,1 6^о448,3

Контрольные вопросы и упражнения:

1. Дать определение прямой и обратной геодезических задач.

2. Дать вывод формул решений прямой (обратной) геодезической задачи.

3. Решить прямую задачу по данным: x₁ =6 104 172,8; y₁ = 5 565 542,8;

s = 4 021,4; α_{1, 2} =57°57'54".

Ответ: x₂ = 6 106 212,4; у₂ = 5 568 802,5.

4. Решить обратную задачу по данным:

x₁ = 6 114 133,5; х₂ = 6 107 134,0; у₁ = 5.565 596,8; у₂ = 5 574 985,3.

Ответ: α_{1, 2} = 126°42'21"; s =11710,5.

5. Решить треугольник по данным:

а) A = 86°49'11"; В = 36°52'12"; в = 7 211,2.	Ответ: С = 56°18'37"; а = 12 000,1; с = 10 000,1.
б) а=5590,2; s = 9 340,7; С = 84°46'51".	Ответ: с = 10 440,2; А = 32°13'26"; В = 62°59'43".
в) а = 10 440,2; в = 12530,0; с = 8 944,2.	Ответ: А = 55°10'30"; В = 80°08'05"; С = 44°41 '25".

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

15 16 17 18 19 20 21

Подборка статей по вашей теме: