Поиск в глубину

При поиске в глубину в качестве активной выбирается та из открытых вершин, которая была посещена последней. Для реализации такого правила выбора наиболее удобной структурой хранения множества открытых вершин является стек: открываемые вершины складываются в стек в том порядке, в каком они посещаются, а в качестве активной выбирается последняя вершина.

Обозначим стек для открытых вершин через S, а верхний элемент стека – через 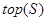. Тогда процедура обхода одной компоненты связности методом поиска в глубину со стартовой вершиной a может быть записана следующим образом (DFS – от Depth First Search).

Procedure DFS(a)

1 Посетить(a);

2 while 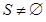do

3 ;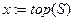

4 if в 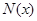имеется неисследованные вершины

5 then выбрать такую вершину ;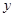

6 if y новая then посетить(y)

7 else удалить 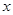из S.

При посещении вершина помечается как посещенная и помещается в стек.

Алгоритм обхода всего графа – тот же, что и в случае поиска в ширину. Остаются верными и оценки трудоемкости: 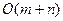, если граф представлен списками смежности, 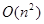, если матрицей смежности.

Поиск в глубину можно применить для нахождения компонент связности графа или для построения каркаса точно таким же образом, как поиск в ширину. Для связного графа каркас с корнем в стартовой вершине, получаемый поиском в глубину, называется DFS-деревом.

Если в некотором связном графе выбран корневой каркас, то все ребра, не принадлежащие каркасу, можно разделить на две категории: ребро назовем продольным, если одна из его вершин является предком другой, в противном случае назовем его поперечным.

Теорема о DFS-дереве. Относительно DFS-дерева все обратные ребра являются продольными.

На этом свойстве основаны многие применения поиска в глубину. Рассмотрим некоторые из них.

Шарнир. Допустим, требуется выяснить, является ли шарниром некоторая вершина х данного графа (предположим, что он связный). Для решения этой задачи достаточно выполнить поиск в глубину со стартом в вершине х и построением DFS-дерева. Если теперь вершину х удалить из графа, то, ввиду отсутствия поперечных ребер, он распадется на столько компонент связности, сколько сыновей у вершины х в DFS-дереве. Значит, вершина х является шарниром тогда и только тогда, когда она имеет в DFS-дереве с корнем х степень 2 или больше.

Все шарниры. Однократным поиском в глубину можно найти все шарниры графа. Будем нумеровать вершины при обходе графа в том порядке, в котором они посещаются. Номер, полученный вершиной 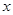, обозначим через 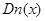, он называется глубинным номером. Введем на множестве вершин еще одну функцию L, связанную с DFS-деревом: значением 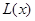является наименьший из глубинных номеров вершин, смежных с потомками вершины х. Если вершина y является сыном вершины x, то 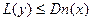(так как вершина y является потомком самой себя и смежна с вершиной x).

Теорема о шарнирах. Корень DFS-дерева является шарниром графа тогда и только тогда, когда его степень в этом дереве больше 1. Вершина x, отличная от корня, является шарниром тогда и только тогда, когда у нее в DFS-дереве имеется такой сын y, что .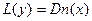

Функцию L можно определить рекурсивно – если мы знаем ее значения для всех сыновей вершины x и глубинные номера всех вершин, смежных с x и не являющихся ее сыновьями, то 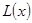есть минимум из всех этих величин, то есть

,

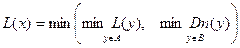где A обозначает множество всех сыновей вершины x, а B – множество всех остальных вершин, смежных с x. Ниже приведена основанная на этом равенстве процедура вычисления функции 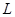и выявления шарниров для одной компоненты связности. Вначале каждой вершине присвоен нулевой глубинный номер и это нулевое значение используется затем как признак того, что вершина новая. Переменная c хранит текущий глубинный номер, вначале 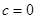. Предполагается, что окрестность каждой вершины реализована в виде списка и запись 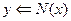означает, что в качестве 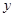берется очередная вершина из списка 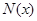и при этом вершина 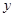из списка удаляется.

Procedure Шарниры(a)

1 посетить(а);

2 while 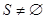do

3 ;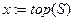

4 if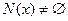

5 then ;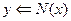

6 if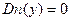

7 then посетить(y)

8 else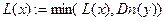

9 else ;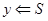

10 if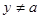

11 then ;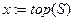

12 if 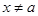then ;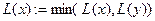

13 if 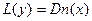then пометить х как шарнир

Procedure Посетить(x)

1 ;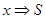

2 ;

3 ;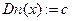

4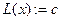

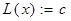
Этот алгоритм находит все шарниры, кроме стартовой вершины а (если она является шарниром). Из теоремы видно, что эта вершина должна обрабатываться особо – нужно просто отслеживать ее степень в DFS-дереве. Это не включено в описание алгоритма, чтобы не загромождать его.

Блоки. Блок графа – это его максимальный связный подграф, не имеющий собственных шарниров (т.е. некоторые шарниры графа могут принадлежать блоку, но своих шарниров у блока нет). Каждое ребро графа принадлежит в точности одному блоку, а вершина может принадлежать нескольким блокам, но только в том случае, когда она – шарнир. Строение связного графа G, состоящего из нескольких блоков, описывается BC-деревом, которое строится следующим образом. В этом дереве вершины двух типов – одни соответствуют блокам графа G (вершины-блоки), другие – его шарнирам (вершины-шарниры). Вершина-блок соединяется в BC-дереве ребром с вершиной-шарниром, если соответствующий шарнир принадлежит соответствующему блоку.

Описанный выше алгоритм выявления шарниров нетрудно приспособить для отыскания всех блоков графа. Достаточно завести еще один стек и складывать в него все посещаемые вершины. При обнаружении шарнира x (строка 13) достаточно извлечь из стека все вершины, содержащиеся в его верхней части вплоть до вершины y и добавить к ним еще вершину x (не удаляя ее, в отличие от других, из стека). Это множество вершин образует очередной блок.