3.2.1. Планирование рациональных путей снабжения методом ветвей
3.2.2. Метод сплошного перебора. Способ фильтров
3.2.3. Методика планирования компромиссных вариантов с использованием игровых моделей
3.2.4. Планирование объектных потоков с непрерывным использованием ресурсов и освоением фронтов.
3.2.1. Задачи, решение которых осуществляется с помощью математических матриц называются матричными.
Рассмотрим некоторые экономико-математические методы матричного планирования.
Задача. Организация снабжает 5 объектов, расположенных как показано на рисунке 3.1 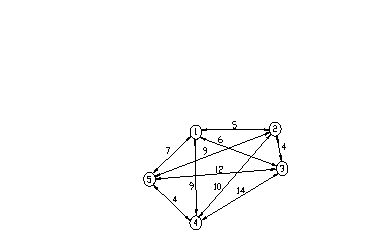
Рисунок 3.1- Схема расположения объектов
Цифрами указано необходимое время для переезда. Требуется найти такой маршрут для снабжения объектов, начинающийся в пункте 1, проходящий через все пункты и заканчивающийся в точке выезда, чтобы его продолжительность была наименьшей.
Для решения задачи составим математическую модель. Для этого введём обозначения;
i и j –номера пунктов въезда и выезда.
tij – продолжительность переезда с объекта i на объект j
Введём переменные, приняв, что
δij= {1, если из пункта i мы идём в пункт j
{0-в противном случае
Приступим к составлению модели. Из пункта 1 можно въехать в любой из пунктов 2-5, но только в одном единственном направлении.
Это условие выглядит так δ11+δ12+δ13+δ14+δ15=1 или Σ δij=1
Рассмотрим последнее условие применительно к произвольному пункту и,
то сможем записать Σδij=1, i=1,5
Это зависимость обеспечивает выполнение условия, что из каждого пункта выезд производится только в одном направлении и только один раз.
Требования минимальной продолжительности маршрута запишется виде целевой функции: L=t11 δ 11 + t12 δ 12+…+ t55 δ 55 →min.
Переходя к сокращённой форме записи рассматриваемую задачу можно сформулировать так:
L=Σ Σ tij δ ij →min
Σ δ ij=1; Σ δ ij=1; i, j =1,5
δij = [0;1]
Решение задачи можно представить в виде квадратной матрицы размерности 5. Общее число возможных вариантов решения задачи 5!=120 для сокращения вычислений используем метод ветвей при котором улучшается значение целевой функции он заключается в следующем: из П.1 мы можем выехать в любой другой пункт, т.е. какая-то одна из булевых переменных δ11,δ12,δ13,δ14,δ15 примет значение 1, тогда все остальные будут равны 0. Допустим δ12 =1, т.е. мы выехали на второй объект; δ13=δ14=δ15=0. Из пункта 2 мы можем выехать в направление 3его, 4ого ил 5ого объектов и т.д.
Дерево возможных маршрутов приведём на рисунке 2. Видно, что всего возможных маршрутов при этом будет 6 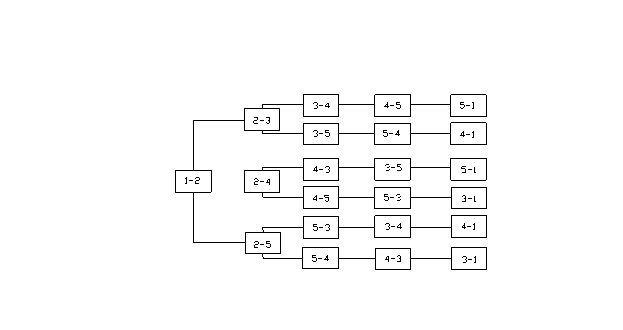
Рисунок 3.2 – Дерево возможных полных маршрутов при первоначальном выезде на второй объект
Таблица 3.1 – Решение математической модели.
| Вариант | Δ12 (δ21) | Δ13 (δ31) | δ14 (δ41) | δ15 (δ51) | δ23 (δ32) | Δ24 (δ42) | Δ25 (δ52) | δ34 (δ43) | δ35 (δ53) | δ45 (δ54) | L | |
| (1) | ||||||||||||
| (1) | (1) | |||||||||||
| (1) | (1) | |||||||||||
| (1) | (1) | |||||||||||
| (1) | (1) | |||||||||||
| (1) | (1) | (1) | ||||||||||
| (1) | (1) | |||||||||||
| (1) | (1) | (1) | ||||||||||
| (1) | (1) | |||||||||||
| (1) | (1) | |||||||||||
| (1) | (1) | |||||||||||
| (1) | (1) | |||||||||||
| (1) | (1) | |||||||||||
| (1) | (1) | (1) | ||||||||||
| (1) | (1) | (1) | ||||||||||
| (1) | (1) | (1) | ||||||||||
| (1) | (1) | |||||||||||
| (1) | (1) | (1) | ||||||||||
| (1) | (1) | |||||||||||
| (1) | (1) | (1) | (1) | |||||||||
| (1) | (1) | (1) | ||||||||||
| (1) | (1) | (1) | ||||||||||
| (1) | (1) | (1) | ||||||||||
| (1) | (1) | (1) | (1) | |||||||||
| tij= tji | ||||||||||||
3.2.2. Задача. Организация может включить в проект производство работ 4 объекта. Для каждого объекта подсчитано потребное количество материальных и трудовых ресурсов, а так же размер прибыли (Таблица 8.2). Требуется выбрать, какие варианты следует реализовать и включить в проект производства работы организации.
Таблица 3.2- Исходные данные к задаче выбора вариантов
| Вариант | Наличие | ||||
| Прибыль | - | ||||
| Ресурсы: | |||||
| Материальные | |||||
| Трудовые |
Для составления модели примем, что j-му варианту будет соответствовать
δj (j=1,4) при этом:
δj {1, если j-й вариант принят
{0, если j-й вариант не принят
Математическая модель задачи будет иметь вид:
{ L=65 δ1+80δ2+90δ3+210δ4→max
200 δ1+180δ2+240δ3+250δ4≤650
10δ1+15δ2+22δ3+28δ4≤50
Решим задачу методом сплошного перебора. Поскольку δj могут принимать значение 0 или 1 в любом сочетании, рассмотрим все возможные сочетания (Таблица 3.3).
Расчёт при полном переборе выполняется в такой последовательности:
1. Заполнить все возможные варианты сочетаний допустимых значений δj
2. Определить значение левых частей ограничений целевых функций и записать их.
3. Вычеркнуть те варианты, в которых не удовлетворяется хотя бы одно ограничение.
4. Из оставшихся вариантов принимается тот в котором целевая функция приобретает максимальное значение.
Таблица 3.3- Решение задачи методом сплошного перебора
| № варианта | Δ1 | δ2 | δ3 | δ4 | Ограниче-ния | L | Примеча-ние | |
| (1) | (2) | |||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| ((300)) | - | |||||||
| (290) | - | |||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| <670> | <65> | - | не допустим | |||||
| <690> | <60> | - | не допустим | |||||
| <53> | - | не допустим | ||||||
| <870> | <75> | - | не допустим | |||||
| Требова-ние | ≤650 | ≤50 |
Оптимальный вариант -восьмой в котором прибыль равна 300 δ1= δ2=0; δ3= δ4=1.
Вместе с тем следует тщательно рассмотреть так же девятый вариант(δ1= δ3=0; δ2= δ4=1), по которому величина прибыли уменьшается от максимально возможной всего на 3,3%, в то время как экономия материальных и трудовых ресурсов составит более 12% и 14% соответственно.
В общем случае число вычисленных процедур для n переменных и m ограничений при полно переборе составит N=2n(m+1).
Для сокращения трудоёмкости при полном переборе предложен способ фильтров. Вычисления ведутся в следующей последовательности.
1. Принимают некоторые значения δj, например δ3=1; δ1= δ2= δ4=0 (по прибыльно к ближайшему к наибольше приближенному)
2. Определяют значение целевой акции при таком переборе: L=90.
В дальнейшем не следует рассматривать варианты, в которых целевая функция принимает меньшие значения. Для этого вводим дополнительное ограничение
65δ1+80 δ2+90 δ3+ 210 δ4≥90,
которое называется фильтром
Далее составляют вышеприведенную таблицу и проверяют для каждого варианта выполнение ограничений.
Вычисление для каждого варианта прекращают в том случае, если не будет выполнено хотябы одно ограничение, включая фильтр. Если вычисление прекращается, и величины не определены, то в клетках таблицы три ставиться прочерк. Введения фильтрирующего ограничения (F) приводит к уменьшению вычислений, в нашем примере с 48 до 36.
3.2.3. В реальной производственной ситуации часто возникают конфликтные ситуации, в которых различные участники имеют несовпадающие между собой интересы (участники тендерных торгов, заказчик и подрядчик генеральный проектировщик и заказчик и т.д.).
Методами обоснования решений в условиях неопределённости и конфликтных ситуаций занимается теория игр.
В теории игр рассматриваются ситуации с двумя участниками, каждый из которых преследует различные и противоположные цели. Во всех таких случаях предполагается, что операция проводится против разумного противника (конкурента), преследующего свои собственные цели и оказывающего сознательное противодействие достижению цели первой стороной.
Какие именно действия предпримет конкурент заранее не известно, но можно уверенно предполагать, что он не сделает ничего такого, что было бы невыгодно ему самому. Это, естественно сужает область неопределённости и упрощает задачу принятия решения.
Целью теории игр является выработка рекомендаций для разумного поведения игроков в конфликтной ситуации, т.е. указание оптимальной стратегии для каждого из них. Рассмотрим платёжную матрицу
Таблица 3.4. - Платёжные матрицы
| Cij | B1 | B2 | … | Bn | αi |
| A1 | C11 | C12 | … | C1n | α1 |
| A2 | C21 | C22 | … | C2n | α2 |
| … | … | … | … | … | … |
| Am | Cm1 | Cm2 | … | Cmn | αm |
| Bj | B1 | B2 | … | Bn | - |
Для нахождения оптимальной стратегии необходимо последовательно проанализировать все возможные стратегии в расчёте на то, что разумный противник на каждую из них будет отвечать такой, при которой выигрыш игрока А минимален. Обычно минимальные числа в каждой строке αi выписываются в виде добавочного столбца в платёжной матрице. В каждой строке будет своё αi =minСij.
Предпочтительно для игрока А является стратегия при которой αi обращается в максимум (α=max αi =max min Сij). Величину α называют максимально выигрышной, а соответствующую ей стратегию максиминной. Она в любом поведении стороны В (противника или конкурента) гарантирует выигрыш не меньший α. Поэтому α называют так же нижней ценой игры- этот гарантированный минимум, который можно обеспечить при наиболее осторожной стратегии.
Аналогичное рассуждение можно провести и для стороны В. Эта сторона должна рассмотреть все свои стратегии, выделяя для каждой из них максимальное значение выигрыша βj=max Сij, которые выписываются в дополнительной строке платёжной матрицы (Таблица 8.1). Следующее из всех значений βj находится минимальное: β=min max Сij.
Величина β даёт минимальный выигрыш (минимакс). Стратегия, соответствующая β называется минимаксной. Она гарантирует стороне В проигрыш не больше β. Поэтому β называют так же верхней ценой игры.
Задача. Проектная организация разработала три варианта железобетонной конструкции: К1,К2,К3. Каждый вариант может быть реализован одним из трёх технологических процессов: (Т1, Т2, Т3). Средние значения прочности конструкции будут практически одинаковы, неоднородность их различная, что скажется в последующем на поведение их в процессе эксплуатации. Если первый конструктивный вариант К1 будет реализован с помощью первого технологического процесса, качество окажется наихудшим и оценивается экспертами в 5 балов. Этот же конструктивный вариант при реализации вторым технологическим процессом Т2 оценивается в 6 балов, а третьим в 9. Оценка для каждого варианта в балах приведена в таблице 3.5.
Таблица 3.5.- Матрица игры для конструктивных и технологических вариантов
| Сij | Технология | ||
| T1 | T2 | T3 | |
| K1 | |||
| K2 | |||
| K3 |
Если проектировщики выберут вариант К1, то «экономисты» будут настаивать на технологии Т1. Но вариант К2 ответ будет Т1 и Т2, так как оба они приводят к одинаковым затратам и дают равноценный результат, оцениваемый в 7 балов. На К3 реакция экономистов будет Т2, дающей 5 балов. Очевидно, что с точки зрения проектировщиков преимущество имеет конструктивный вариант К2, так как даже при неблагоприятных обстоятельствах получиться конструкция оцениваемая в 7 балов.
Встанем теперь на позицию «экономистов» и посмотрим, какой тех. Процесс для них наиболее выгоден с точки зрения снижения затрат. Если выбрать Т1, то при конструктивном варианте К3 затраты окажутся наибольшими- 8 балов при варианте Т2 может быть вариант К2 с затратами 7, при Т3 конструктивный вариант К1, требующий затрат 9. Таким образом, для «экономистов» оптимальным является технологический процесс Т2, поскольку он требует меньше затрат при различных конструктивных вариантах. Следовательно в данном примере стратегии К2Т2 с выигрышем 7 является наиболее выгодным для обеих сторон- максимальный выигрыш К совпадает с минимальным выигрышем Т.
3.2.4. В основе расчете всех потоков лежит положение о том, что работа может выполняться только при обязательном выполнении условий: должны быть свободны фронт работ и соответствующий ресурс, т.е. специализированный отряд, выполняющий данный вид работ, должен завершить работы на предыдущем участке и быть готовым для выполнения работ на рассматриваемом частном фронте.
Ресурсная связь показывает характер движения ресурса (специализированного отряда) с участка на участок, а фронтальное освобождение (степень готовности) частного фронта работ.
Рассчитать поток – это означает определить сроки выполнения всех видов работ на каждом участке.
Для формирования потока с непрерывным использованием ресурсов необходимо в процессе расчета обеспечить нулевое растяжение ресурсной связи (Rрс)
Расчет матрицы при организации работ с непрерывным использованием ресурсов производится по строкам (видам работ) в следующей последовательности:
А) прямым ходом определяются возможные сроки выполнения j-го вида работ: Tnij=max (Toi-1,j; Toi,j-1)
Toij = Tnij + tij,
тем самым обеспечивается выполнения обязательного условия о наличии ресурса и готовности фронта работ;
Б) обратным ходом определяются расчётные сроки выполнения j-го вида работ при непрерывном использовании ресурсов: Toij = Tni+1,j; Tnij = Toij – tij,
тем самым обеспечивается непрерывное использование ресурсов.
В) в соответствии с указанным алгоритмом производится расчёт следующей строки и т.д.
Если в матрице имеются пустые клетки (т.е. на каких-то фронтах не выполняются какие либо работы), то принимается срок окончания предшествующей фактической работы.
Потоки с непрерывным освоением фронтов менее характерны. Их особенность заключается в том, что без простоев используется частные фронты работ, т.е. на участке после изменения одного вида работ сразу же выполняется следующий такой организации работ могут вычитывать ресурсы, кроме случая режима потока. Этот метод используется в моделях с комбинированной организацией работ, где на паре смежных видов работ по техническим или организационным причинам необходимо работать с простоем фронтов.
Для метода организации работ с непрерывным освоением фронтов расчёт матрицы производится по столбцам следующим образом:
А) определяются возможные сроки выполнения работ на i-ом фронте по формулам пункта А предыдущего раздела;
Б) определяются расчётные сроки выполнения работ на i-ом фронте: срок окончания работ Toij = Tni,j+1; срок начала работ Tnij = Toij – tij, тем самым обеспечивается непрерывность освоения фронтов;
В) определяются сроки выполнения работ следующих столбцов повторением пунктов А) и Б).
 2014-02-04
2014-02-04 599
599








