Локальная и интегральная теоремы Лапласа

Случайные величины Х_i, введенные при рассмотрении схемы Бернулли, независимы и одинаково распределены с математическим ожиданием М (Х_i) = р и дисперсией 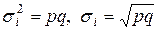. Таким образом, случайную величину 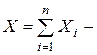число появлений “успеха” в n независимых испытаниях – можно считать при больших n приближенно нормально распределенной с математическим ожиданием 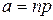и дисперсией 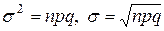. Тогда при больших n вероятность события { X = k } можно приближенно положить равной значению функции плотности вероятности в точке .

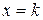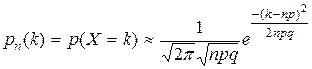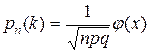. Если обозначить через х выражение , то , где 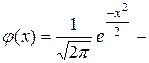функция плотности вероятности центрированного и нормированного нормального распределения. Этот результат называется локальной теоремой Лапласа. Вероятность события 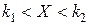(< или £ - это неважно) при больших значениях n можно вычислить через значения функции Лапласа

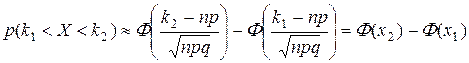, (12.6)

где , .

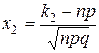Этот результат называется интегральной теоремой Лапласа.

Выведенные формулы дают хорошее приближение к истинным значениям вероятностей тогда, когда n достаточно велико (50 и более), а вероятность р не слишком отличается от 0,5 в ту или иную сторону. Практически можно судить о возможности замены биноминального распределения нормальным по тому, выполнены ли при данных n и р условия

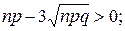
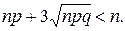
Эти условия основаны на “правиле трех сигм” для нормального закона (задача 102), когда они соблюдены, можно пользоваться нормальным распределением.