Интерпретация в логике первого порядка
Необходимо соотнести формулы логики предикатов первого порядка и предикаты. Как и в логике высказываний подобное соотнесение осуществляет функция, называемая интерпретацией.
Определение. Интерпретацией на непустом множестве М называется функция, заданная на сигнатуре FÈR, которая
1) константе ставит в соответствие элемент из М;
2) символу n-местной функции ставит в соответствие некоторую n-местную функцию, определенную на множестве М;
3) символу n-местного предиката ставит в соответствие n-местный предикат, заданный на М.
В результате любая формула F получает в соответствие предикат, местность которого равна числу свободных переменных формулы F.
Приведем примеры. Пусть сигнатура состоит из символа одноместного предиката P и двухместного предиката D, M={2,3,6,9,12,15} и
F=(P(x)&("y)(P(y)®D(x,y))
Поставим в соответствие (проинтерпретируем) P(x) предикат «x – простое число», D(x,y) – предикат «x меньше или равно y». Тогда формула F получит в соответствие предикат «x=2». На этом же множестве можно рассмотреть и другую интерпретацию: P(x) ставится в соответствие «x – нечетное число», D(x,y) – предикат «x делит y». В таком случае, формула F получает в соответствие предикат «x=3». Если j – интерпретация, то предикат, соответствующий формуле F будем обозначать через j(F).
Одним из основных типов задач этой темы являются задачи, связанные с использованием выразительных возможностей языка логики предикатов. В качестве примера рассмотрим задачу перевода на язык логики предикатов следующего рассуждения. «Каждый первокурсник знаком с кем-либо из спортсменов. Никакой первокурсник не знаком ни с одном любителем подледного лова. Следовательно, никто из спортсменов не является любителем подледного лова». Для удобства ссылок это рассуждение условимся называть рассуждением о первокурсниках. Выберем следующую сигнатуру:
П(х): «х – первокурсник»,
С(х): «х – спортсмен»,
Л(х): «х – любитель подледного лова»,
З(x,y): «х знаком с y».
Тогда рассуждение запишется в виде следующей последовательности формул.
Н1=("x)[П(х)®($y)(C(y)&З(x,y))],
H2=("x)("y)[П(x)&Л(y)®ØЗ(x,y)],
H3=("x)(C(x)®ØЛ(x))
Мы установили, что выразительных средств логики предикатов достаточно, чтобы записать рассуждение о первокурсниках. Естественно далее поставить вопрос, логично ли оно? Будет ли третье предложение следствием первых двух? На этот вопрос мы ответим в §5.
Общая схема изложения материала этого и двух следующих параграфов будет напоминать изложение материала в §3-5 темы 1.
Определение. Формулы F(x1,…,xn) и G(x1,…,xn) называются равносильными, если для любой интерпретации j с областью М высказывания (jF)(a1,…,an) и (jG)(a1,…,an) при любых a1,…,an из М одновременно истинны или одновременно ложны.
Пусть F(x)=Ø("y)P(x,y), G(x)=($y)ØP(x,y), где Р – символ двухместного предиката. Докажем, что формулы F(x) и G(x) равносильны. Возьмем интерпретацию j с областью М. Пусть высказывание (jF)(a) истинно для aÎM. Истинность этого высказывания одначает, что не для всякого yÎM высказывание (jP)(a,y) истинно. Следовательно, найдется bÎM, для которого высказывание (jP)(a,b) ложно. Если высказывание (jP)(a,b), ложно, то высказывание Ø(jP)(a,b) истинно. Отсюда следует, что найдется yÎM такой, для которого высказывание Ø(jP)(a,y) истинно. Это означает истинность высказывания (jG)(a). Итак, мы доказали, что если высказывание (jF)(a) истинно, то высказывание (jG)(a) тоже истинно. Обратная импликация доказывается аналогично. Значения истинности высказываний (jF)(a) и (jG)(a) при любом aÎM совпадают. Следовательно, формулы F(x) и G(x) равносильны.
Определение. Формула F(x1,…,xn) называется тождественно истинной, если для любой интерпретации j с областью М высказывание (jF)(a1,…,an) при любых a1,…,an из М является истинным.
Как и в случае логики высказываний. Приведем список основных равносильностей – законов логики предикатов. Прежде всего, получим законы логики предикатов из законов 1–21 логики высказываний, понимая под F,G,H – произвольные формулы логики предикатов. Дополним полученный список законами, специфичными для логики предикатов
22) ("x)(F(x)&G(x) равносильна ("x)(F(x)&("x)G(x),
23) ($x)(F(x)ÚG(x) равносильна ($x)F(x)Ú($x)G(x),
24) ("x)("y)F(x,y) равносильна ("y)("x)F(x,y),
25) ($x)($y)F(x,y) равносильна ($y)($x)F(x,y),
26) Ø("x)F(x) равносильна ($x)ØF(x),
27) Ø($x)F(x) равносильна ("x)ØF(x).
Законы 21,22 утверждают, что квантор общности можно переносить через конъюнкцию, а квантор существования через – дизъюнкцию. Естественно поставить вопрос, можно ли квантор существования переносить через конъюнкцию, а квантор общности – через дизъюнкцию. Другими словами, будут ли равносильны следующие пары формул
("x)(F(x)ÚG(x) и ("x)(F(x)Ú("x)G(x)
($x)(F(x)&G(x) и ($x)(F(x)& ($x)G(x)?
Оказывается нет. Докажем это для случая, когда F(x) и G(x) – атомарные формулы. Пусть основное множество – множество натуральных чисел N, F(x) – предикат «x – четное число», G(x) – предикат «x – нечетное число». Обозначим эту интерпретацию буквой j. Тогда j("x)(F(x)ÚG(x))]=1, но j[("x)F(x)Ú("x)G(x)=0. Аналогично, j($x)(F(x)&G(x))]=0 и j($x)F(x)&($x)G(x)]=1.
Рассмотрим законы 23 и 24. Они утверждают, что одноименные кванторы можно менять местами. Можно ли переставлять местами разноименные кванторы, сохраняя равносильность. Другими словами, равносильны ли формулы
("x)($y)(F(x,y) и ($y)("x)F(x,y)?
Оказывается, тоже нет. В качестве основного множеств авозьмнм опять множнство натуральных чисел, F(x,y) будем считать атомарной формулой и поставим ей в соответствие предикат «x меньше y». Тогда левая формула будет истинной, правая – ложной.
Вернемся к законам 21 и 22. Мы отмечали, что квантор существования – через конъюнкцию. Тем не менее, если одна из формул F или G не содержит переменной x, то это делать можно. Запишем соответствующие законы:
28) ("x)(F(x)ÚG) равносильна ("x)(F(x)ÚG,
29) ($x)(F(x)&G) равносильна ($x)(F(x)&G, где G не содержит x.
Законы 21, 22, 28, 29 можно записать в общем виде:
30) (Q1x)(Q2z)(F(x)ÚG(z)) равносильна (Q1x)F(x)Ú(Q2z)G(z)
31) (Q1x)(Q2u)(F(x)&G(u)) равносильна (Q1x)F(x)&(Q2u)G(u),
где Q1, Q2 кванторы V или Э, u не входит в F(x), а x не входит в G(u). Для доказательства равносильности двух формул могут оказаться полезными следующие законы:
Рассмотрим формулу F(x)=("y)P(x,y)®P(x,c), где P – символ двухместного отношения, с – константа. Докажем, что формула F(x) тоэждественно истинна. Возьмем интерпретацию j с областью М и элемент а из М. Высказывание (jF)(a) равно ("y)(jP)(a,y)®(jP)(a,j(c)). Если посылка ("y)(jP)(a,y) ложна, то вся импликация (jF)(a) истинна. Предположим, что посылка ("y)(jP)(a,y) истинна. Это означает, что для всякого yÎM высказывание (jP)(a,y) истинно, в том числе истинно это высказывание и для y=j(c). Следовательно, истинно заключение (jP)(a,j(c)) и вся импликация (jF)(a). Мы доказали, что высказывание (jF)(a) истинно для любого aÎM. Это означает, что формула F(x) является тождественно истинной.
Понятия равносильности и тождественной истинности в логике первого порядка связаны точно так же, как и в логике высказываний.
Теорема 3.1 Формулы F(x1,…,xn) и G(x1,…,xn) равносильны тогда и только тогда, когда формулы F(x1,…,xn)«G(x1,…,xn) тождественно истинны.
Доказательство теоремы 3.1 аналогично доказательству теоремы 1.1 и поэтому не приводится
32) ("x)F(x) равносильна ("z)F(z),
33) ($x)F(x) равносильна ($z)F(z).
В законах 32 и 33 переменная z не входит в F(x), а переменная x не входит в F(z).
В логике высказываний мы применяли два способа доказательства равносильности формул: построение совместной таблицы истинности и переход от одной формулы к другой с помощью законов. В случае логики первого порядка остается только второй способ.
Проиллюстрируем его на примере следующей задачи: доказать равносильность формул:
F=Ø("x)($y)[S(x)&P(x,y)®($z)(T(z)&P(x,z))]
G=($x)("y)[S(x)&P(x,y)&("z)(T(z)®ØP(x,z))].
Применим к формуле F последовательно законы 26, 27 и 20, получим, что формула F равносильна формуле
F1=($x)("y)Ø[Ø(S(x)&P(x,y))Ú($z)(T(z)&P(x,z))].
Далее, используя закрны 18,19 и 27 из F1, получим формулу
F2=($x)("y)[S(x)&P(x,y)&("z)Ø(T(z)&P(x,z))].
Осталось заметить, что в силу законов 17 и 20 в формуле F2 подформулу Ø(T(z)&P(x,z)) можно заменить на T(z)®ØP(x,z).
Подчеркнем, что доказательство равносильности двух формул будем проводить с помощью законов логики первого порядка. Доказательство того, что формулы неравносильны, будем осуществлять построением интерпретации, при которой одна формула истинна, другая ложна. Например, так, как это было сделано выше для доказательства неравносильности формул ("x)(F(x)ÚG(x)) и ("x)F(x)Ú("x)G(x). Разумеется, до построения интерпретации формулы можно предварительно преобразовывать с помощью законов.
I:
S: Логическая функция, принимающая значения в некоторой области истинностных значений: ###
I:
S: Комбинация знаков, содержащая знаки переменных, которая превращается в высказывание при замене переменных именами предметов: ###
I:
S: Переменные, фигурирующие в кванторах всеобщности и существования:
-: связанные
-: свободные
-: существенные
-: определяющие
I:
S: Функция, равная единице тогда и только тогда, когда предикат истинен:
-: характеристическая
-: правильная
-: вырожденная
-: определенная
I:
S: Язык логики предикатов является расширением языка:
-: логики высказываний
-: модальной логики
-: нечеткой логики
-: формальной логики
I:
S: Для составления предикатных функций используют:
-: высказывания
-: алгоритмы
-: функции
-: формулы
I:
S: Пусть предикат Р(х;у) описывает отношение «х любит у», тогда высказывание «Все люди любят всех людей» записывается формулой:
-: 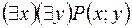
-: 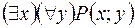
-: 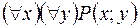
-: 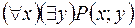
I:
S: Пусть предикат Р(х;у) описывает отношение «х любит у», тогда высказывание «Существует человек, который кого-то любит» записывается формулой:
-: 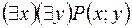
-: 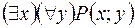
-: 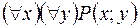
-: 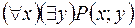
I:
S: Пусть Q(х;у) – предикат порядка «х ≤ у», тогда высказывание «Для любых х и у выполняется неравенство х ≤ у» запишется формулой:
+: 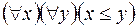
-: 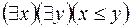
-: 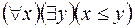
-: 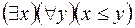
I:
S: Пусть Q(х;у) – предикат порядка «х ≤ у», тогда высказывание «Существуют такие х и у, что х ≤ у» запишется формулой:
-: 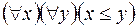
-: 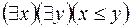
-: 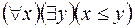
-: 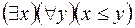
I:
S: Дан предикат Р(х;у) – «х делится на у», определенный на множестве натуральных чисел. Высказывание 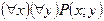 формулируется:
формулируется:
-: существует два числа х и у, такие, что х делится на у
-: для всякого натурального числа существует такое натуральное число, на которое оно делится
-: любое натуральное число делится на любое натуральное число
-: существует натуральное число, которое делится на любое натуральное число
I:
S: Дан предикат Р(х;у) – «х делится на у», определенный на множестве натуральных чисел. Высказывание 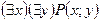 формулируется:
формулируется:
-: любое натуральное число делится на любое натуральное число
-: существует два числа х и у, такие, что х делится на у
-: для всякого натурального числа существует такое натуральное число, на которое оно делится
-: существует натуральное число, которое делится на любое натуральное число
I:
S: Дан предикат Р(х;у) – «х делится на у», определенный на множестве натуральных чисел. Высказывание 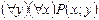 формулируется:
формулируется:
-: существует натуральное число, которое является делителем какого-нибудь натурального числа
-: все натуральные числа являются делителями для всех натуральных чисел
-: существует натуральное число, которое является делителем любого натурального числа
-: для всякого натурального числа найдется такое натуральное, которое делится на первое
I:
S: Дан предикат Р(х;у) – «х делится на у», определенный на множестве натуральных чисел. Высказывание 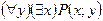 формулируется:
формулируется:
-: все натуральные числа являются делителями для всех натуральных чисел
-: существует натуральное число, которое является делителем какого-нибудь натурального числа
-: существует натуральное число, которое является делителем любого натурального числа
-: для всякого натурального числа найдется такое натуральное число, которое делится на первое
I:
S: Равносильная формула для формулы логики предикатов 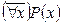 :
:
-: 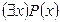
-: 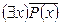
-: 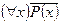
-: 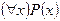
I:
S: Равносильная формула для формулы логики предикатов 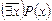 :
:
-: 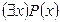
-: 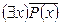
-: 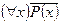
-: 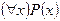
I:
S: Равносильная формула для формулы логики предикатов 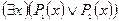 :
:
-: 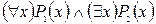
-: 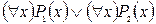
-: 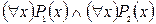
-: 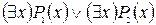
I:
S: Равносильная формула для формулы логики предикатов 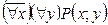 :
:
-: 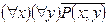
-: 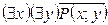
-: 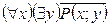
-: 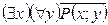
I:
S: Равносильная формула для формулы логики предикатов 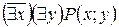 :
:
-: 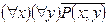
-: 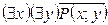
-: 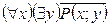
-: 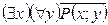
I:
S: Равносильная формула для формулы логики предикатов 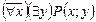 :
:
-: 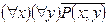
-: 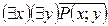
-: 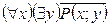
-: 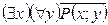
I:
S: Отрицанием высказывания 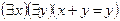 , где х
, где х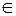 R и у
R и у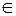 R является высказывание:
R является высказывание:
-: 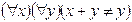
-: 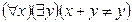
-: 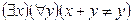
-: 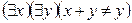
I:
S: Отрицанием высказывания 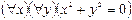 , где х
, где х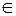 R и у
R и у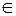 R является высказывание:
R является высказывание:
-: 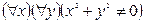
-: 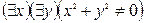
-: 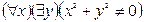
-: 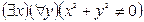
I:
S: Отрицанием высказывания 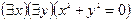 , где х
, где х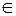 R и у
R и у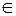 R является высказывание:
R является высказывание:
-: 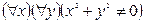
-: 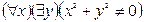
-: 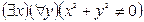
-: 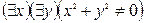
I:
S: Отрицанием высказывания 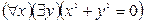 , где х
, где х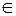 R и у
R и у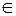 R является высказывание:
R является высказывание:
-: 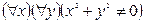
-: 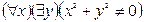
-: 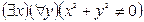
-: 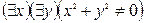
I:
S: Отрицанием высказывания 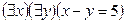 , где х
, где х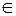 R и у
R и у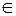 R является высказывание:
R является высказывание:
-: 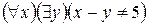
-: 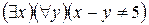
-: 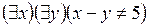
-: 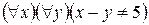
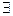 х) Р(х) = (
х) Р(х) = (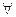 х) Р(х)-: ⌐(
х) Р(х)-: ⌐(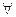 х) Р(х) = (
х) Р(х) = (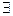 х) ⌐Р(х)-: ⌐(
х) ⌐Р(х)-: ⌐(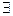 х) Р(х) = (
х) Р(х) = (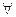 х) ⌐Р(х)-: ⌐(
х) ⌐Р(х)-: ⌐(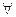 х) Р(х) = (
х) Р(х) = (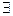 х) Р(х) I:S: Правило отрицания квантора существования имеет вид:-: ⌐(
х) Р(х) I:S: Правило отрицания квантора существования имеет вид:-: ⌐(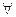 х) Р(х) = (
х) Р(х) = (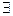 х) ⌐Р(х)-: ⌐(
х) ⌐Р(х)-: ⌐(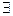 х) Р(х) = (
х) Р(х) = (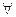 х) ⌐Р(х)-: ⌐(
х) ⌐Р(х)-: ⌐(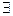 х) Р(х) = (
х) Р(х) = (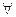 х) Р(х)-: ⌐(
х) Р(х)-: ⌐(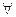 х) Р(х) = (
х) Р(х) = (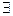 х) Р(х) I: S: Связанным является вхождение переменной:-: в область действия квантора-: стоящей непосредственно за квантором, в область действия квантора-: стоящей непосредственно за квантором, в выражение, содержащее квантор-: стоящей непосредственно перед квантором, в область действия квантора
х) Р(х) I: S: Связанным является вхождение переменной:-: в область действия квантора-: стоящей непосредственно за квантором, в область действия квантора-: стоящей непосредственно за квантором, в выражение, содержащее квантор-: стоящей непосредственно перед квантором, в область действия квантора I:
Q: Соответствие предикатом области истинности для чисел натурального ряда:
L1: x + 5 = 1
R1: –4
L2: x2 < 4
R2: -2 < 0 < 2
L3: x2 – 1 = 0
R3: +1
R4: -1
I:
S: Принимающая значения в некоторой области истинностных значений логическая функция: ###
I:
S: Высказывание – это предикатная:+: константа-: переменная-: форма-: сущность 2014-02-02
2014-02-02 1318
1318







