Функции алгебры логики

Рассмотриммножество векторов X = {<x₁... x_n>}. Будем предполагать, что координаты этих векторов могут принимать значения 0 или 1. Таким образом, множество X состоит из 2ⁿ векторов. Произведем отображение множества X в множество Y = {0, 1} [1].

Определение. Функцией алгебры логики называется функция, дающая однозначное отображение X в Y.

Определение. Если две функции алгебры логики f₁(x₁... x_n) и

f₂(x₁... x_n) принимают на всех наборах значений аргументов одинаковые значения, то их называют равными

Определение. Функция f(x₁... x_n) существенно зависит от аргумента x_i, если имеет место соотношение: f(x_1... x_i-1, 0, x_i+1... x_n) ¹ f(x_1... x_i-1, 1, x_i+1... x_n). В противном случае x_i - фиктивный аргумент.

Теорема 1. Число различных функций алгебры логики, зависящих от n аргументов конечно и равно 2ⁿ.

Приведем иллюстрацию сказанного на основе анализа таблицы:

Таблица 1.6

x1, x2,..., xn	f(x1, x2,..., xn)
00...00	a1
00...01	a2
00...10	a3
...	...
11...11	a2n

Как показывает таблица, задавая тот или иной конкретный двоичный набор аргументов, задается одна из возможных функций алгебры логики, принимающая значение 0 или 1. Различное число таких наборов равно 2ⁿ. Следовательно, число функций будет равно 2ⁿ.

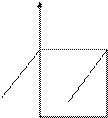
Рассмотрим геометрическую интерпретацию области определения функции алгебры логики. Сопоставим наборам аргументов алгебры логики точки n-мерного пространства. Тогда множество 2ⁿ таких наборов определит множество вершин n- мерного единичного куба. Таким образом, множество вершин n- мерного единичного куба есть область определения функций алгебры логики. Пусть вершина А соответствует набору

(х1 = 1, х2 = 1, х3 = 1), а вершина B - набору (х1 = 1, х2 = 1, х3 = 0).

Тогда графически это может быть представлено следующим рисунком:

X3

A

0 X2

B

X1

Рис. 1.1. Геометрическая интерпретация области определения логических функций

Рассмотрим основные функции, которые играют основную роль в построении функций алгебры логики и ее приложениях:

1. f = X.

2. f = ØX

3. f = 0.

4. f = 1.

5. f = X v Y.

6. f = X & Y.

7. f = X ~ Y (равенство, эквивалентность).

8. f = X ® Y (импликация).

9. f = X ¯ Y (стрелка Пирса, функция Вебба).

10. f = X | Y (штрих Шеффера).

11. f = X Å Y (сложение по модулю 2).

Эти одиннадцать функций алгебры логики позволяют строить новые функции, при этом используется два подхода: - подстановка в функцию новой функции вместо аргументов и переобозначение аргументов.

Определение. Функция, полученная из f₁... f_k путем применения возможно многократно указанных двух подходов называется суперпозицией функций f₁... f_k.

Пример. Представить в виде таблицы функцию

f (X1, X2) = { (X1 ¯ X2) v (X1 Å X2) } = X1 | X2.

Решение.

X1	X2	X1 ¯ X2	X1 Å X2	X1 | X2.

Пример. Показать, что

X1 ® X2 = ØX1 v X2 на основе построения и сравнения функций по таблицам истинности.

Решение.

X1	X2	X1 ® X2	ØX1	ØX1 v X2

Аналогично можно показать, что сложение по модулю 2:

X1 Å X2 = Ø ((ØX1 v X2) & (X1 v ØX2)).

А функция эквивалентности: X ~ Y = (ØX1 v X2) & (X1 v ØX2), т.е. эти 2 функции связанны отношением отрицания.

Ø(ØX1) = X.

X1 & X2 = Ø (ØX1 v ØX2).

X1 v X2 = Ø (ØX1 & ØX2).

Рассмотрим свойства конъюнкции, дизъюнкции и отрицания.