Метод моментов для экспоненциального и нормального законов

Непрерывная случайная величина 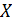, принимающая неотрицательные значения, имеет экспоненциальное распределение с параметром 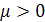, если ее функция плотности равна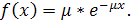

На рисунке 12 приведены функция распределения 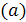и функция плотности экспоненциального закона при .

class=WordSection2>

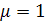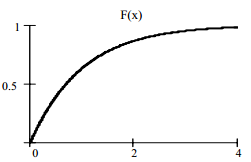
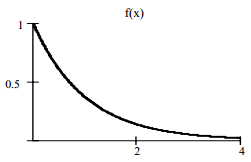
Рисунок 12.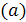

Первый начальный момент: 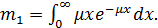Применив интегрирование по частям, вычислим, что этот интеграл равен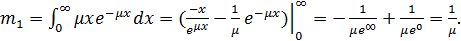

Второй начальный момент: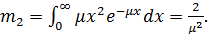

Среднее квадратическое отклонение:

Непрерывная случайная величина 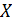имеет нормальное распределение с параметрам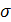и и 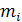, если ее функция плотности равна 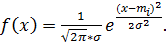Т.е. в качестве параметров в функцию плотности входят математическое ожидание и среднее квадратическое отклонение. Поэтому для использования метода моментов достаточно в данную формулу подставить их оценки, вычисленные по экспериментальному распределению. Для оценки качества аппроксимации по критериям согласия Пирсона и Колмогорова требуется вычислить вероятность попадания случайной величины в интервалы гистограммы и гипотетическую функцию распределения. Так как интеграл от функции плотности нормального закона аналитически «не берется», то он определяется по таблицам, составленным для нормального закона с математическим ожиданием, равным нулю, и среднеквадратическим отклонением, равным единице, с преобразованием реального распределения по следующим формулам: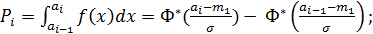

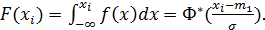
На рисунке 13 приведены функция распределения 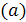и функция плотности нормального закона при

class=WordSection3>

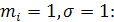
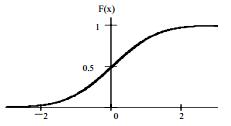
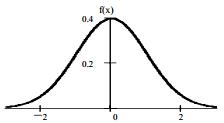
Рисунок 13.