Условия независимости линейного интеграла от формы пути

В различных приложениях важно знать, зависит ли линейный интеграл поля 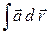от формы кривой интегрирования или он зависит только от начальной и конечной точек этой кривой (с физической точки зрения – зависит ли работа силы от формы пути). Рассмотрим три условия независимости линейного интеграла поля от формы пути интегрирования. Как и раньше, будем предполагать, что вектор-функция 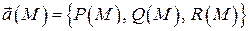дифференцируема.

Теорема (о равенстве нулю циркуляции). Для того чтобы линейный интеграл поля не зависел от формы пути интегрирования, необходимо и достаточно, чтобы циркуляция поля по любой замкнутой кривой равнялась нулю.

Доказательство. Вычислим циркуляцию поля по произвольной замкнутой кривой (рис. 8)

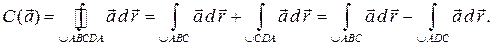
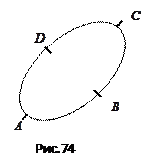Из этого равенства следует: циркуляция 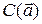равна нулю тогда и только тогда, когда 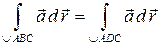, т. е. интеграл 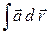по двум произвольным линиям с общим началом и общим концом принимает одно и то же значение и, значит, не зависит от формы пути интегрирования.

Рис. 8

Теорема дает критерий независимости линейного интеграла поля от формы пути интегрирования, однако этот критерий трудно проверить.

Для формулировки следующего более эффективного критерия введем новое понятие. Область назовем односвязной, если на любой ее замкнутый контур можно натянуть поверхность, целиком лежащую в этой области.

Например, односвязными областями будут круг, шар, куб; к неодносвязным областям относятся кольцо, тор (“бублик”) (рис. 9).

Теорема (о равенстве нулю ротора). Для того чтобы линейный интеграл поля не зависел от формы пути интегрирования, необходимо, а для односвязного поля и достаточно, чтобы ротор поля в каждой точке равнялся нулю.

Необходимость. Пусть линейный интеграл поля не зависит от формы пути интегрирования и, значит, циркуляция 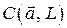по любому замкнутому контуру равна нулю. Тогда по формуле

,

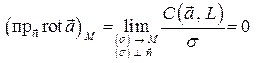т.е. проекция ротора на любой вектор 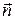в любой точке равна нулю. Поэтому

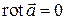в любой точке поля.

Достаточность. Пусть 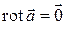в односвязной области . Возьмем любой замкнутый контур в 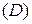. В силу односвязности области 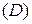на контур 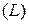можно натянуть поверхность , целиком лежащую в области 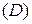. Вычислим циркуляцию поля по контуру 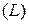, используя формулу Стокса и условие :

.

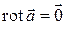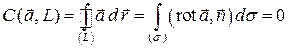Так как циркуляция поля по любому замкнутому контуру 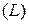равна нулю, то

по теореме интеграл 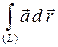не зависит от формы пути. Теорема доказана.

Теорема (о подынтегральном выражении). Для того чтобы линейный интеграл поля 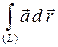не зависел от формы пути интегрирования, необходимо и достаточно, чтобы подынтегральное выражение 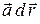было полным дифференциалом некоторой функции .

Необходимость. Пусть 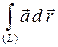не зависит от формы пути. Покажем, что функция 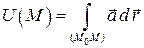есть искомая функция (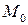─ фиксированная точка), т.е. .

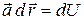Для этого вычислим частное приращение

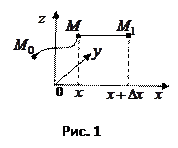
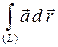Так как интеграл не зависит от формы пути, то кривую 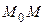выберем произвольно, а в качестве кривой 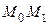возьмем кривую 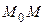и отрезок прямой (рис. 1). Тогда по свойству аддитивности интеграла

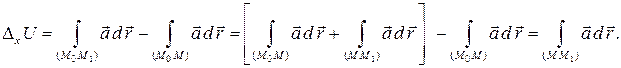
Запишем интеграл в координатной форме и учтем, что на отрезке меняется только , а постоянны, значит, и

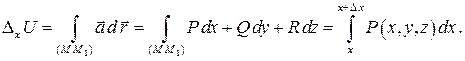
К получившемуся определенному интегралу применим теорему о среднем:

;

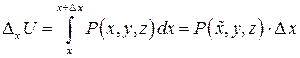здесь 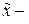некоторая промежуточная точка между и 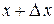. Тогда

.

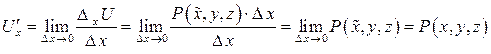Итак, 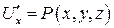. Аналогично можно показать, что 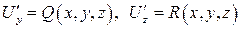. Тогда .

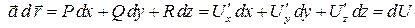Достаточность. Пусть существует функция 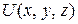такая, что .

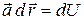Рассмотрим произвольную дугу 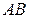с параметрическими уравнениями

.

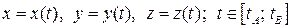Сведем интеграл 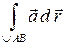по этой дуге к определенному интегралу и применим формулу Ньютона-Лейбница

.

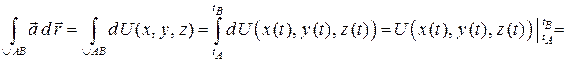
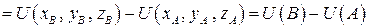Таким образом, значение интеграла 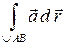зависит только от точек 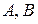и не зависит от формы линии .

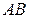16. Лекционное занятие. ПОТЕНЦИАЛЬНОЕ ПОЛЕ

Как и раньше, предполагаем, что координаты вектора поля ─ функции 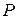, , 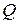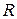непрерывны и имеют частные производные.

Векторное поле называется потенциальным, если оно является полем градиента некоторой скалярной функции 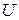, т.е. 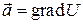; при этом функцию 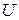называют скалярным потенциалом векторного поля.

Напомним, что 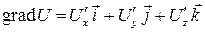. Так как 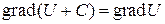, то 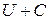также является потенциалом.