Функц-ные ряды, область сходимости функц-ного ряда. Понятие равномерной сходимости. Мажорируемые ряды. Признак Вейерштрасса равномерной сходимости рядов. Интегрирование и диф-ние функц-х рядов.
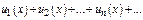 .
.
Такие ряды наз-т функц-ми. Предполагается, что 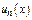 определены и непрерывны. Для одних знач-й
определены и непрерывны. Для одних знач-й 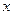 ряд может сходится, для других – расходиться. При знач-и
ряд может сходится, для других – расходиться. При знач-и  получим числовой ряд
получим числовой ряд 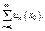 Если он сходится, то точка
Если он сходится, то точка 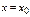 наз-ся точкой сходимости функц-го ряда. Совок-ть всех точек сходимости наз-ся обл-ю сходимости функц-го ряда. Обл-ь сходимости – интервал оси
наз-ся точкой сходимости функц-го ряда. Совок-ть всех точек сходимости наз-ся обл-ю сходимости функц-го ряда. Обл-ь сходимости – интервал оси 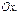
Пример. 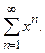 Ряд сходится в области
Ряд сходится в области 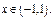 При
При  ряд расходится.
ряд расходится.
Сумма ряда 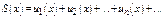 есть ф-я независимой перем-й
есть ф-я независимой перем-й 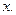 В примере
В примере 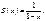 Эта ф-я есть сумма только при
Эта ф-я есть сумма только при 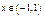
Частичная сумма 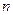 первых членов ряда обозначается
первых членов ряда обозначается 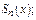 остаток ряда -
остаток ряда - 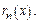 Если ряд сходится при каком-либо
Если ряд сходится при каком-либо 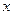 , то
, то 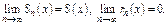
При конечном числе ф-й интеграл или производная от суммы равна сумме интегралов или производных. Для ряда этого может и не иметь место.
Опред-е. Функц-й ряд 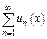 наз-ся равномерно сходящимся в обл-ти
наз-ся равномерно сходящимся в обл-ти 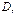 если
если 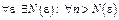 выполняется нер-во
выполняется нер-во 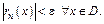
Признак Вейерштрасса равномерной сходимости рядов. Ряд 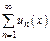 равномерно сходится в обл-ти
равномерно сходится в обл-ти 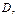 если сущ-ет сходящийся числовой ряд
если сущ-ет сходящийся числовой ряд 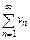 такой, что
такой, что 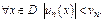 В этом случае ряд
В этом случае ряд 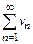 наз-т мажорантой ряда
наз-т мажорантой ряда 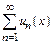 или мажорирующим рядом.
или мажорирующим рядом.
Примеры. 1) 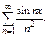
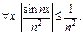 Т. к. ряд
Т. к. ряд 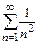 сходится, то ряд
сходится, то ряд 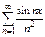 сходится равномерно.
сходится равномерно.
2) 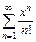 сходится
сходится 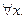 Сумма ряда равна
Сумма ряда равна  Эта сходимость равномерная для любой конечной области
Эта сходимость равномерная для любой конечной области 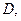 т. к.
т. к. 
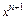 растет медленнее
растет медленнее 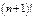 Для всей числовой оси сходимость неравномерная, т. к.
Для всей числовой оси сходимость неравномерная, т. к. 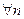 можно найти такое
можно найти такое 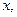 что
что 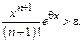
 2014-02-02
2014-02-02 591
591








