Расстояния между городами

Город
	∞
		∞
			∞
				∞
					∞

Например, расстояние из города 2 в город 3 равно 4 единицам, а из города 4 в город 5 – 8 единицам. По диагонали таблицы установлены символы, обозначающие бесконечность, что свидетельствует о невозможности такого передвижения коммивояжера.

В соответствии с утверждением 1: если все элементы первой строки таблицы уменьшить на 4 (наименьшее значение в строке), то это не повлияет на порядок городов в кратчайшем кольцевом маршруте, проходящем через все города по одному разу, а лишь сократит его длину на 4. Будем называть эту операцию приведением таблицы по строке, а число 4 – константой приведения. Аналогично можно поступить со всеми строками таблицы. На рис. 8.2, а изображена таблица до приведения ее по всем строкам. Столбец, помеченный символом 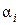, содержит константы приведения для каждой строки, а под столбцом в окружности указана сумма этих констант (число 13). На рис. 8.2, б изображена таблица после приведения ее по всем строкам.

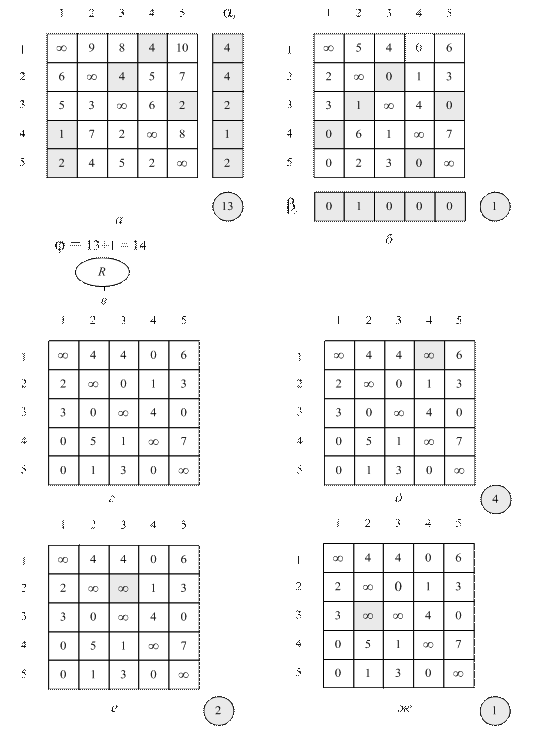
Рис. 8.2. Приведение матриц в задаче коммивояжера (окончание см. на с. 195) а – таблица до приведения ее по всем строкам; б – таблица после приведения ее по всем строкам; в – корневая вершина дерева T; г – таблица, приведенной по строкам и по столбцам; д – таблица расстояний между городами, по которой невозможно построить конечный кольцевой маршрут, содержащий дугу (1, 4); е и ж – аналогично исследуются все дуги таблицы на рис. г, имеющие нулевую длину

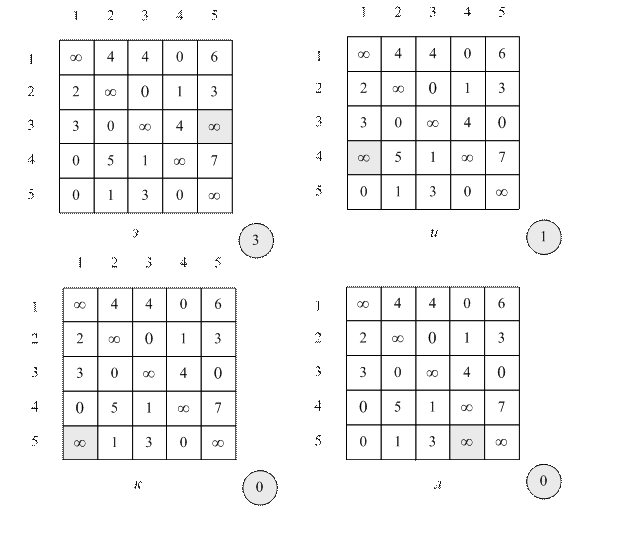Рис. 8.2. Окончание. з – л аналогично исследуются все дуги таблицы на рис. г, имеющие нулевую длину

В соответствии с утверждением 2: если все элементы второго столбца таблицы на рис. 8.2, б уменьшить на 1 (наименьшее значение в столбце), то это не повлияет на порядок городов в кратчайшем кольцевом маршруте, проходящем через все города по одному разу, а лишь сократит его длину на 1. Будем называть эту операцию приведением таблицы по столбцу, а число 1 – константой приведения. Аналогично можно поступить со всеми столбцами таблицы на рис. 8.2, б. Столбец, помеченный символом 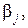содержит константы приведения для каждого столбца, а в окружности указана сумма этих констант (число 1). Таблица на рис. 8.2, г является таблицей, приведенной по строкам и по столбцам. Далее будем называть такие таблицы полностью приведенными таблицами.

Общая сумма констант приведения равна 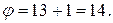Эту величину можно принять в качестве нижней границы длины кратчайшего кольцевого маршрута, проходящего через все города (далее просто – кратчайший кольцевой маршрут).

На рис. 8.2, в изображена корневая вершина дерева T, соответствующая множеству 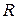– всех допустимых решений данной задачи (множеству всех кольцевых маршрутов, проходящих через все города по одному разу).

Прежде чем будет применена процедура ветвления BR, оценим, как будет изменяться нижняя граница подмножеств, полученных после применения процедуры BR в зависимости от выбора дуги, которая используется для разбиения. Наибольший интерес представляет та дуга, которая наиболее сильно может повлиять на нижнюю границу длины допустимых кольцевых маршрутов.

Несложно понять, что анализировать, прежде всего, следует дуги, имеющие нулевой вес, так как только их удаление может повлиять на нижнюю границу. Удаление дуги может быть промоделировано установкой ее веса равного бесконечности.

На рис. 8.2, д изображена таблица расстояний между городами, по которой невозможно построить конечный кольцевой маршрут, содержащий дугу (1, 4). Таблица на рис. 8.2, д получена из таблицы на рис. 8.2г заменой элемента первой строки четвертого столбца на символ бесконечности. В окружности на рис. 8.2, д указана сумма констант приведения для этой таблицы (4). Другими словами, если считать, что среди допустимых кольцевых маршрутов нет дуги (1, 4), то нижняя граница увеличится на 4. На рис. 8.2, е –8.2, л аналогично исследуются все дуги таблицы на рис. 8.2, г, имеющие нулевую длину.

Вычисления показывают, что удаление дуги (1, 4) позволяет получить самую большую сумму констант приведения (4), а значит, выбор этой дуги для ветвления с помощью процедуры BR даст самую большое увеличение нижней границы длины кольцевых маршрутов. Или проще, все допустимые кольцевые маршруты 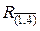, которые могут быть построены по таблице на рис. 8.2, д не будут включать путь из города 1 в город 4, а длина этих кольцевых маршрутов не будем меньше, чем нижняя граница, построенная для таблицы на рис. 8.2, г увеличенная на 4.

На рис. 8.3 изображен фрагмент графа T, который может быть построен на этом этапе решения задачи.

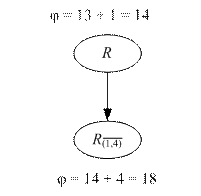
Рис. 8.3. Фрагмент графа T

Вторая ветвь решения, полученная процедурой BR,соответствует множеству допустимых кольцевых маршрутов, которые включают дугу (1, 4). Если дуга (1, 4) включается в кольцевой маршрут, то по всей видимости, следует этот факт запомнить и построить новую таблицу, в которой будет отсутствовать первая строка (во всех допустимых маршрутах из города 1 есть дуга только в город 4) и четвертый столбец (в город 4 есть единственная дуга и это дуга из города 1). Кроме того, очевидно, что допустимый кольцевой маршрут, содержащий дугу (1, 4), не может содержать дугу (4, 1), так как наличие этих двух дуг в кольцевом маршруте делает его недопустимым. Из этого следует, что на пересечении четверной строки и первого столбца надо поставить символ бесконечности. На рис. 8.4, а изображена таблица, полученная из таблицы на рис. 8.2, г вычеркиванием из нее первой строки, четвертого столбца и заменой значения в первом столбце четвертой строки на символ бесконечности. Сумма констант приведения, подсчитанная для этой таблицы, равна 1. На рис. 8.4, б изображена таблица, которая получена после приведения таблицы на рис. 8.4, а.

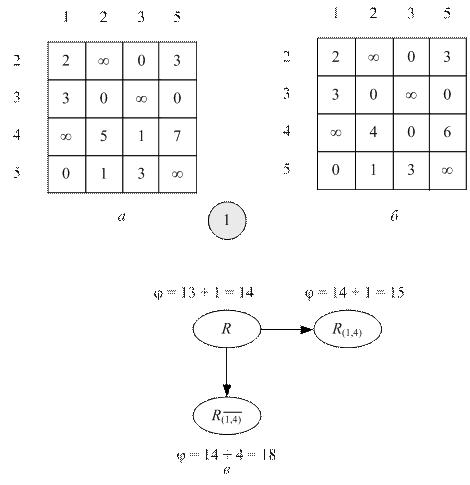
Рис. 8.4 Построение второй ветви графа T

а – таблица, полученная из таблицы на рис. 8.2, г вычеркиванием из нее первой строки, четвертого столбца и заменой значения в первом столбце четвертой строки на символ бесконечности; б – таблица, которая получена после приведения таблицы на рис. 8.4, а; в – фрагмент графа T, имеющий две ветви

На рис. 8.4, в изображен фрагмент графа T, имеющий две ветви. Нижняя граница дочерних узлов, вычисляется как сумма, нижней границы родительского узла и суммы констант приведения соответствующей таблицы.

Согласно алгоритму (см. разд. 8.1) дальнейший поиск решения следует осуществлять во множестве 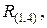поскольку именно здесь на текущий момент нижняя граница является меньшей.

Проанализировав таблицу на рис. 8.4, б, несложно вычислить, что удаление дуги (4, 3) позволит получить наибольшую сумму констант приведения (4).

На рис. 8.5, а изображена таблица, полученная из таблицы на рис. 8.4, б заменой нулевого значения в четвертой строке третьего столбца на символ бесконечности. Сумма констант приведения для этой таблицы равна 4. На рис. 8.5, б представлена таблица, полученная из таблицы на рис. 8.5, а путем полного ее приведения.

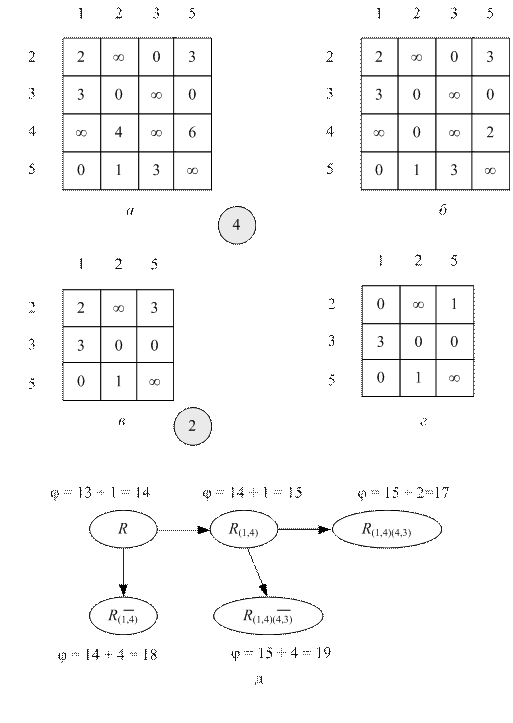
Рис. 8.5. Построение третьей и четвертой ветвей графа T

Таблица на рис. 8.5, в получена из таблицы на рис. 8.4, б путем вычеркивания четвертой строки и третьего столбца. Сумма констант приведения этой таблицы равна 2. На рис. 8.5, г изображена таблица, полученная из таблицы на рис. 8.5, в путем полного ее приведения.

На рис. 8.5, д изображен фрагмент графа T,который построен на основе графа, показанного на рис. 8.4, в. Две добавленные ветви соответствуют множествам 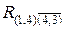(множество допустимых кольцевых маршрутов, содержащих дуги (1, 4) и не содержащих дуги (4, 3)) и 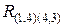(множество допустимых кольцевых маршрутов, содержащих одновременно дуги (1, 4) и (4, 3)).

Дальнейший поиск решения целесообразно осуществлять во множестве 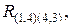так как здесь на текущий момент нижняя граница является меньшей. На рис. 8.6 изображен еще один шаг построения графа T. Анализ таблицы на рис. 8.5, г позволяет выявить дугу (2, 1), удаление которой приводит к максимальной сумме констант приведения (1). Следует отметить, что удаление дуги (5, 1) тоже даст такую же сумму констант приведения. В этом случае может быть выбрана любая из дуг.

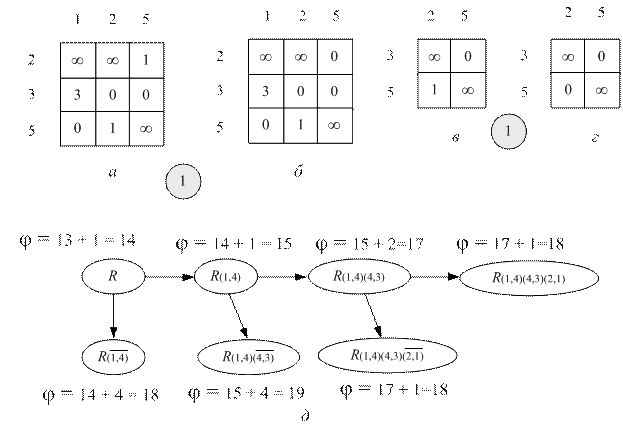Рис. 8.6. Построение пятой и шестой ветвей графа T

Таблица на рис. 8.6, а получена из таблицы на рис. 8.5, г заменой элемента второй строки первого столбца на символ бесконечности. Таблица на рис. 8.6, б является полностью приведенной таблицей на рис. 8.6, а.

Таблица на рис. 8.6, в получена из таблицы на рис. 8.5, г удалением второй строки и первого столбца (это соответствует включению дуги в кольцевой маршрут), а также заменой значения в третьей строке второго столбца на символ бесконечности (позволяет блокировать образование неполного кольцевого маршрута). На рис. 8.6, г представлена таблица, полученная из таблицы на рис.8.6, в, после ее полного приведения. На рис. 8.6, д изображен очередной фрагмент графа T после добавления двух ветвей.

Граф T,изображенное на рис. 8.6, д, содержит три вершины, которым соответствует одинаковое значение нижней границы (18). В этом случае целесообразно продолжать наращивать ветви графа, начиная с вершин, наиболее удаленных от корня. В нашем случае была выбрана вершина 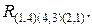Анализ таблицы на рис. 8.6, г позволяет выявить два последних звена кольцевого маршрута: (3, 5) и (5, 2). Эта таблица не может быть приведена, т. е. сумма констант приведения будет равной 0.

На рис. 8.7 изображен окончательный вид графа T.

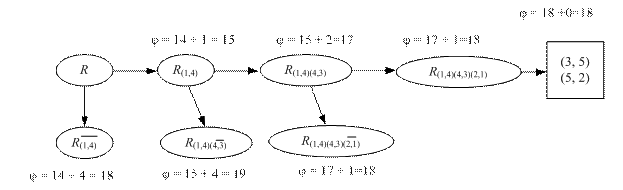
Рис. 8.7. Граф решения T задачи коммивояжера

Для получения окончательного решения следует расставить выбранные дуги в правильном порядке: (1, 4), (4, 3), (3, 5), (5, 2), (2, 1). Сложив расстояния (таблица), соответствующие дугам кольцевого маршрута, получим 18, что совпадает с нижней границей, приписанной последнему узлу графа T (рис. 8.7).

Следует обратить внимание на несколько листовых вершин дерева на рис. 8.7, которым тоже соответствует нижняя граница, равная 18. Продолжение вычислений для этих ветвей в лучшем случае приведет к получению кольцевого маршрута такой же длины (18), но никогда меньшей.