Теорема Чебышева

Теор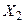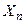ема Чебышева. Если , , …, – попарно независимые случайные величины, причём дисперсии их равномерно ограничены (не превышают постоянного числа С), то для любого сколь угодно малого 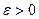вероятность неравенства 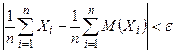будет сколь угодно близка к единице, если число случайных величин достаточно велико: .

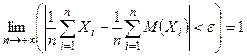Замечание. Теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно мало.

Доказательство. Обозначим случайную величину 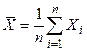– среднее арифметическое рассматриваемых случайных величин. Её математическое ожидание 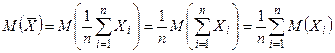. Применяя к 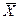неравенство Чебышева, имеем:

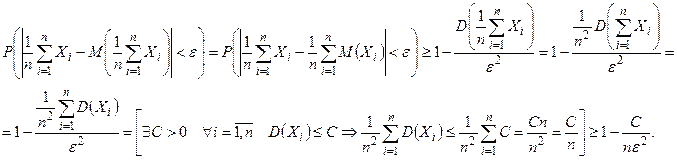
Тогда 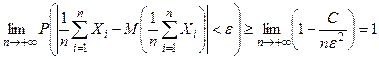. Так как вероятность любого события не превосходит 1, то .

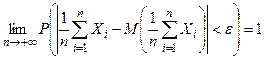Следствие. Если , , 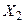…, 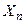– попарно независимые случайные величины, имеющие одно и то же математическое ожидание 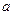, причём дисперсии их равномерно ограничены (не превышают постоянного числа С), то для любого сколь угодно малого 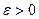вероятность неравенства 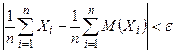будет сколь угодно близка к единице, если число случайных величин достаточно велико: .

Замечание 1. Отдельные независимые случайные величины могут принимать значения далёкие от своих математических ожиданий, а среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения, близкие к среднему арифметическому их математических ожиданий. Т.е. случайные величины могут иметь значительный разброс, а их среднее арифметическое расс е яно м а ло. Следовательно, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предсказать, какое значение примет их среднее арифметическое. Другими словами, среднее арифметическое достаточно большого числа независимых случайных величин, дисперсии которых равномерно ограничены, утрачивает характер случайной величины. Объясняется это тем, что отклонения случайных величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются. Теорема справедлива как для дискретных, так и для непрерывных случайных величин.

Замечание 2. Применение теоремы Чебышева.

1) Теория измерений. Отдельные измерения рассматриваются как случайные величины. К этим величинам применяется теорема Чебышева, если величины попарно независимы (результаты одного измерения не влияют на результаты другого), имеют одно и то же математическое ожидание (измерительный прибор не даёт систематической ошибки), дисперсии их равномерно ограничены (прибор обеспечивает определённую точность измерений). Тогда среднее арифметическое значений, полученных при измерении, принимается за истинное значение измеряемой величины.

2) Выборочный метод в математической статистике. По небольшой случайной выборке судят о всей генеральной совокупности изучаемых объектов.