Глава 3. ВЕКТОРНЫЕ ФУНКЦИИ
Контрольные вопросы
1.Что относится к государственной тайне?
2. Каков перечень сведений составляющих государственную тайну, отнесение сведений к государственной тайне?
3. Что представляет собой система защиты государственной тайны?
4. Какова процедура оформления права граждан на доступ к сведениям, составляющим государственную тайну?
5. Кто утверждает(ют) государственные программы в области защиты государственной тайны?
6. Что не подлежит к засекречиванию и отнесению к государственной тайне?
7. Кто обосновывает необходимость отнесения сведений к государственной тайне?
8. Что является основанием для рассекречивания сведений, составляющих государственную тайну?
9. Какие существуют степени секретности информации, отнесенной к государственной тайне?
10. Как осуществляется допуск должностных лиц и граждан РФ к государственной тайне?
11. Какие существуют формы допуска в соответствии со степенями секретности сведений, составляющих государственную тайну?
|
|
|
12. Для кого существует особый порядок допуска к сведениям, составляющим государственную тайну?
13. Каковы основания для отказа должностному лицу или гражданину в допуске к государственной тайне?
14. Кто организует исполнение закона «О государственной тайне»?
15. Кто осуществляет надзор за соблюдением закона «О государственной тайне»?
16. Кто осуществляет контроль обеспечения защиты государственной тайны.
17.Основные понятия, информационные ресурсы, пользование ими, информационные системы. Виды тайн в российском законодательстве.
Пусть Х и Y – два множества, f – отображение Х в Y, т.е. некоторое правило, в силу которого каждому элементу 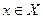 в множестве Y соответствует единственный элемент y =
в множестве Y соответствует единственный элемент y = 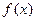 . Элементы множеств Х и Y могут быть любыми математическими обьектами: числами (вещественными или комплексными), векторами, матрицами и т.п. Иногда термину “отображение” предпочитают термин “функция”. В частности, если Х представляет собой некоторое числовое множество, отображение
. Элементы множеств Х и Y могут быть любыми математическими обьектами: числами (вещественными или комплексными), векторами, матрицами и т.п. Иногда термину “отображение” предпочитают термин “функция”. В частности, если Х представляет собой некоторое числовое множество, отображение 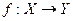 чаще на- зывают функцией аргумента х,
чаще на- зывают функцией аргумента х, 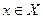 . Если при этом элементы множества Y также яв-ляются числами, f называют числовой или скалярной функцией; о таких функциях шла речь в предыдущих параграфах. Если же множество Y состоит из векторов, отоб- ражение
. Если при этом элементы множества Y также яв-ляются числами, f называют числовой или скалярной функцией; о таких функциях шла речь в предыдущих параграфах. Если же множество Y состоит из векторов, отоб- ражение 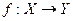 называют векторной функцией или, короче, вектор-функцией.
называют векторной функцией или, короче, вектор-функцией.
Математическое понятие вектор-функции можно иллюстрировать разнообраз- ными примерами векторных величин, вэятыми из механики, физики и других естест- венных наук. Так, хаотичное броуновское движение малой частицы вызвано тем, что вектор действующей на неё силы (равнодействующей столкновений частицы с молеку- лами жидкости или газа) ежемоментно меняется и по направлению, и по величине. Эту силу можно рассматривать как вектор-функцию, аргументом которой является время.
|
|
|
В этом параграфе изложены основы дифференциального исчисления вектор-функций.
1.1. Основные понятия
Пусть Т – некоторое множество вещественных чисел, и пусть на Т определена вектор-функция 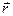 (t), т.е. сформулировано некоторое правило, согласно которому каж-дому
(t), т.е. сформулировано некоторое правило, согласно которому каж-дому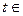 Т соответствует единственный вектор
Т соответствует единственный вектор 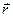 =
= 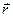 (t).. Обозначим через x (t), y(t) и z (t) проекции вектора
(t).. Обозначим через x (t), y(t) и z (t) проекции вектора 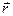 (t) на координатные оси соответственно абсцисс, ординат и ап- пликат декартовой прямоугольной системы координат. Очевидно, x (t), y(t) и z (t) – ска- лярные функции, определенные на множестве Т, причём на Т справедливо разложе- ние вектора
(t) на координатные оси соответственно абсцисс, ординат и ап- пликат декартовой прямоугольной системы координат. Очевидно, x (t), y(t) и z (t) – ска- лярные функции, определенные на множестве Т, причём на Т справедливо разложе- ние вектора 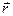 (t) по базису, составленному из ортов координатных осей:
(t) по базису, составленному из ортов координатных осей: 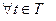
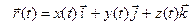 = (x (t), y (t), z (t)).
= (x (t), y (t), z (t)).
Функции x (t), y(t) и z (t) называют координатными функциями вектор-функции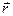 (t). Следовательно, если на множестве Т определена вектор-функция
(t). Следовательно, если на множестве Т определена вектор-функция 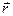 (t), то на Т определена и упорядоченная тройка (x (t), y(t), z (t)) её координатных (скалярных) функ- ций.
(t), то на Т определена и упорядоченная тройка (x (t), y(t), z (t)) её координатных (скалярных) функ- ций.
Заметим, что справедливо и обратное: если (x (t), y (t), z (t)) - упорядоченная тройка каких-то скалярных функций, определенных на Т, то на Т можно определить вектор-функцию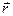 (t) с помощью равенства:
(t) с помощью равенства: 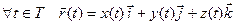 . Таким образом, задание на каком-либо множествевектор-функции эквивалентно заданию на этом множестве упорядоченной тройки скалярных функций.
. Таким образом, задание на каком-либо множествевектор-функции эквивалентно заданию на этом множестве упорядоченной тройки скалярных функций.
Может оказаться, что все значения 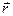 (t),
(t), 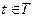 , компланарны, т.е. параллельны некоторой плоскости. Введя на этой плоскости декартову прямоугольную систему координат, получим:
, компланарны, т.е. параллельны некоторой плоскости. Введя на этой плоскости декартову прямоугольную систему координат, получим: 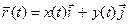 , где
, где 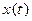 и
и 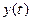 – проекции вектора
– проекции вектора 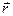 (t) на оси Ox и Oy соответственно. Таким образом, в этом случае задание на множестве T,
(t) на оси Ox и Oy соответственно. Таким образом, в этом случае задание на множестве T, 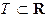 , вектор- функции
, вектор- функции 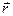 (t) эквивалентно заданию на T упорядоченной пары скаляр- ных функций:
(t) эквивалентно заданию на T упорядоченной пары скаляр- ных функций: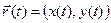 . Можно, конечно, и здесь считать, что на T задана упорядоченная тройка функций
. Можно, конечно, и здесь считать, что на T задана упорядоченная тройка функций 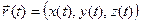 , причем
, причем 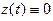 на T. Везде ниже мы связываем задание вектор- функции с заданием упорядоченной тройки скалярных функций.
на T. Везде ниже мы связываем задание вектор- функции с заданием упорядоченной тройки скалярных функций.
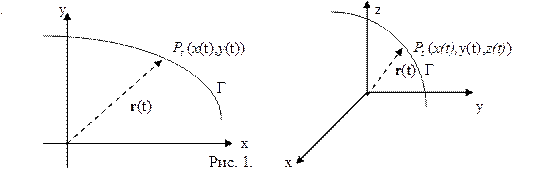 Удобной геометрической интерпретацией вектор- функции является её годограф.По- местим начало вектора
Удобной геометрической интерпретацией вектор- функции является её годограф.По- местим начало вектора  (t) в начало координат и обозначим его конец через
(t) в начало координат и обозначим его конец через  За- метим, что координатные функции образуют набор координат этой точки:
За- метим, что координатные функции образуют набор координат этой точки: (x (t), y (t), z (t)). Когда t, возрастая, пробегает множество T, точка
(x (t), y (t), z (t)). Когда t, возрастая, пробегает множество T, точка 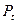 перемещается, описывая некоторую кривую Г (см. рис. 1). Эту кривую и называют годографом вектор- функции
перемещается, описывая некоторую кривую Г (см. рис. 1). Эту кривую и называют годографом вектор- функции 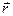 (t). Переменную t называют параметром кривой Г, уравнения x = x (t), y = y (t), z = z (t) – параметрическими уравнениями кривой Г Систему
(t). Переменную t называют параметром кривой Г, уравнения x = x (t), y = y (t), z = z (t) – параметрическими уравнениями кривой Г Систему
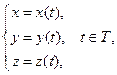 будем называть координатной формой уравнения кривой Г, а эквивалентное этой сис- теме векторное уравнение
будем называть координатной формой уравнения кривой Г, а эквивалентное этой сис- теме векторное уравнение 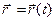 ,
, 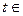 Т, где
Т, где 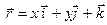 , - векторной формой уравнения этой кривой.
, - векторной формой уравнения этой кривой.
Пример 1. Пусть 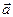 =
= 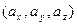 и
и 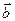 =
=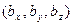 ,
, 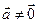 – заданные векторы. Отложим
– заданные векторы. Отложим 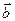 из начала координат O и обозначим через D прямую, проходящую через конец вектора
из начала координат O и обозначим через D прямую, проходящую через конец вектора 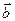 , точку В
, точку В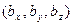 параллельно
параллельно 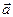 . При всяком вещественном t поло- жим:
. При всяком вещественном t поло- жим: 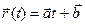 . Прямая D является годографом. этой вектор- функции, а система
. Прямая D является годографом. этой вектор- функции, а система
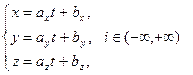 - координатной формой уравнения прямой.
- координатной формой уравнения прямой.
1.2. Предел вектор- функции в точке
Пусть t0 – вещественное число, а  - вектор- функция определенная в проко- лотой окрестности
- вектор- функция определенная в проко- лотой окрестности 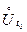 Пусть, далее,
Пусть, далее,  - некоторый вектор.
- некоторый вектор.
Определение. Вектор  называют пределом вектор-функции
называют пределом вектор-функции  при t, стремя- щемся к t0 , если для любого ε> 0 можно указать δ> 0 такое, что при всех t, принадлежа- щих проколотой δ – окрестности
при t, стремя- щемся к t0 , если для любого ε> 0 можно указать δ> 0 такое, что при всех t, принадлежа- щих проколотой δ – окрестности 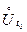 точки t0, длина разности векторов
точки t0, длина разности векторов  и
и  меньше ε..
меньше ε..
Если  удовлетворяет условиям этого определения, будем записывать:
удовлетворяет условиям этого определения, будем записывать:  =
= 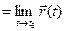 (
( является пределом
является пределом  при t, стремящемся к t0 ) или
при t, стремящемся к t0 ) или 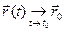 (
( стремится к
стремится к  при t, стремящемся к t0 ).
при t, стремящемся к t0 ).
Итак, равенство 
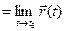 по определению означает:
по определению означает:

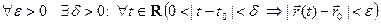 ,
,
где | t- t0 | есть модуль разности двух чисел, а | -
-  | - длина разности двух векторов (см. рис. 2)
| - длина разности двух векторов (см. рис. 2)
Замечание. Обозначим: φ (t) =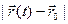 . Очевидно, φ (t) - скалярная функция, определённая в проколотой окрестности
. Очевидно, φ (t) - скалярная функция, определённая в проколотой окрестности 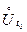 , причём (см. выше)
, причём (см. выше)
|
|
|
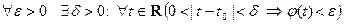 , т.е.,
, т.е., 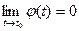 (см. определение предела скалярной функции на языке «ε-δ»). Таким образом,
(см. определение предела скалярной функции на языке «ε-δ»). Таким образом, 
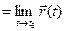 тогда и только тогда, когда длина разности
тогда и только тогда, когда длина разности  -
-  является бесконечно малой при t
является бесконечно малой при t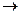 t0:
t0:
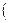

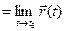
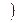
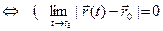
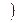 . (1)
. (1)
Теорема 1 устанавливает связь между пределом вектор-функции и пределами её координатных функций
Теорема 1. (О покоординатной сходимости) Пусть вектор-функция  опре- делена в проколотой окрестности
опре- делена в проколотой окрестности 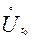 точки t0 , t0
точки t0 , t0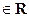 , а x (t), y (t) и z (t) - её координат- ные функции. Пусть, далее,
, а x (t), y (t) и z (t) - её координат- ные функции. Пусть, далее,  - некоторый вектор, а
- некоторый вектор, а 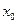 ,
, 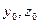 его координаты. Вектор
его координаты. Вектор  является пределом вектор-функции
является пределом вектор-функции  при
при 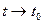 тогда и только тогда, когда его координаты являются пределами при
тогда и только тогда, когда его координаты являются пределами при 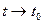 соответствующих координатных функций:
соответствующих координатных функций:
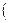

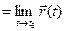
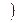
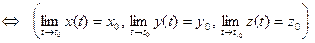
►Имеем:  =(
=(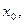
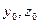 ) и
) и 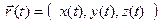 . Отсюда:
. Отсюда:
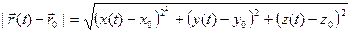 . Подкоренное выражение представляет собой сумму трёх неотрицательных слагаемых; поэтому левая часть этого равенства стремится к нулю при
. Подкоренное выражение представляет собой сумму трёх неотрицательных слагаемых; поэтому левая часть этого равенства стремится к нулю при 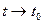 тогда и только тогда, когда каждое из этих слагаемых стремится к нулю при
тогда и только тогда, когда каждое из этих слагаемых стремится к нулю при 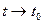 , т.е.
, т.е.
(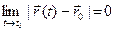 )
) 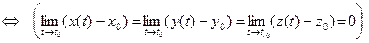 , что можно переписать так:
, что можно переписать так:
|
(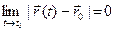 )
) 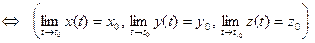 (2) Утверждение теоремы следует из (1) и (2). ◄
(2) Утверждение теоремы следует из (1) и (2). ◄
Следствие. Если 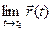 =
= , то
, то 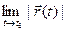 =|
=| |. ►
|. ► 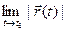 =
= 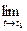
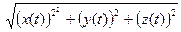 =
= 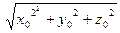 = |
= | |. ◄
|. ◄
Замечание. Если 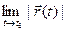 =|
=| |, то вовсе не обязательно справедливо равенство
|, то вовсе не обязательно справедливо равенство 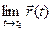 =
= . Вместе с тем, справедливо утверждение:
. Вместе с тем, справедливо утверждение:
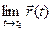 =
=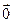
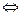
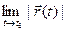 = 0
= 0
- это вытекает из (1) как частный случай при  =
= 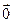 .
.
Опираясь на теорему о покоординатной сходимости можно доказывать теоремы о пределах вектор-функций, аналогичные теоремам о пределах скалярных функций.
Теорема 2. (О единственности предела) Если вектор-функция  имеет пре- дел при
имеет пре- дел при 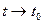 , то только один.
, то только один.
► Допустим, что вектор-функция 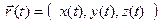 имеет при при
имеет при при 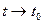 два различных предела:
два различных предела:  =(
=(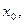
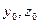 ) и
) и 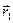 =(
=(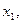
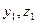 ). Так как
). Так как  ≠
≠ 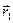 , то упорядо- ченные тройки их координат не могут совпадать. Пусть, к примеру,
, то упорядо- ченные тройки их координат не могут совпадать. Пусть, к примеру, 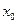 ≠
≠ 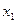 . В силу тео- ремы о покоординатной сходимости координатная функция x (t) должна при
. В силу тео- ремы о покоординатной сходимости координатная функция x (t) должна при 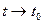 стремиться и к
стремиться и к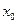 , и к
, и к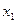 ; но это противоречит теореме о единственности предела ска- лярной функции. ◄
; но это противоречит теореме о единственности предела ска- лярной функции. ◄
Теорема 3. (О действиях над пределами вектор-функций) Пусть в проколотой окрестности 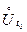 точки t0 , t0
точки t0 , t0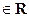 , определены вектор-функции
, определены вектор-функции 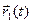 и
и 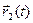 и скалярная функция λ (t), и пусть эти функции имеют пределы при
и скалярная функция λ (t), и пусть эти функции имеют пределы при 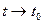 :
: 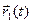
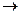
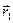 ,
, 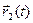
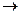
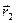 λ (t)
λ (t) 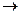 λ. Тогда:
λ. Тогда:
|
|
|
1) 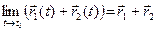 ; 2)
; 2) 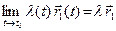 ;
;
3) 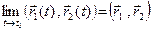 ; 4)
; 4) 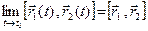 .
.
► Доказательства всех четырёх утверждений проводятся по единой схеме, по- этому достаточно продемонстрировать одно из них. Изложим доказательство утверж- дения 4).
Запишем разложения векторов 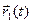 ,
, 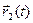 ,
, 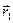 и
и 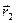 по базису
по базису 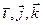 , составлено- му из ортов координатных осей:
, составлено- му из ортов координатных осей:
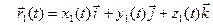 ,
, 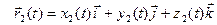 ,
,
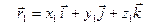 ,
, 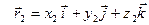 . Используя формулу векторной алгебры, запишем разложение вектора векторного про- изведения
. Используя формулу векторной алгебры, запишем разложение вектора векторного про- изведения 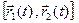 :
:
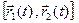 =
= 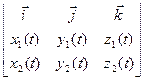 =
=
= 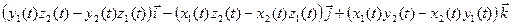 Из теоремы об арифметических действиях с пределами скалярных функций и теоремы о покоординатной сходимости следует:
Из теоремы об арифметических действиях с пределами скалярных функций и теоремы о покоординатной сходимости следует:
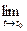
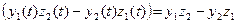 ;
;
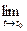
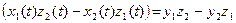 ;
;
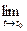
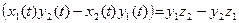 . Опираясь на эти равенства и теорему о покоординатной сходимости, теперь получим:
. Опираясь на эти равенства и теорему о покоординатной сходимости, теперь получим:
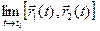 =
= 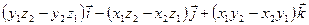 =
=  . ◄
. ◄
Замечание. Для векторов не определены отношения «больше» или «меньше»; утверждение «вектор  больше вектора
больше вектора 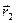 » смысла не имеет. По этой причине среди теорем о вектор-функциях нет аналогов тех теорем о пределах скалярных функций, формулировки которых содержат неравенства, а именно, теоремы о предельном пере- ходе в неравенстве, о стабилизации знака неравенства, о «сжатой» функции.
» смысла не имеет. По этой причине среди теорем о вектор-функциях нет аналогов тех теорем о пределах скалярных функций, формулировки которых содержат неравенства, а именно, теоремы о предельном пере- ходе в неравенстве, о стабилизации знака неравенства, о «сжатой» функции.
Пусть вектор-функция  определена на интервале (α,β),
определена на интервале (α,β),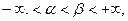 а
а  - некоторый вектор.
- некоторый вектор.
Определение. Вектор  назовём односторонним пределом вектор-функции
назовём односторонним пределом вектор-функции  при t, стремящемся к α справа (при t, стремящемся к β слева), если для любого ε> 0 можно указать δ> 0 такое, что при всех t, принадлежащих интервалу (α, α + δ)
при t, стремящемся к α справа (при t, стремящемся к β слева), если для любого ε> 0 можно указать δ> 0 такое, что при всех t, принадлежащих интервалу (α, α + δ) 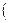 при- надлежащих интервалу (
при- надлежащих интервалу (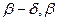 )
)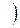 , длина разности
, длина разности  -
- меньше ε.
меньше ε.
Пусть вектор-функция  определена на интервале (α,β),
определена на интервале (α,β),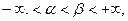 а x (t), y (t) и z (t) - её координатные функции. Пусть, далее,
а x (t), y (t) и z (t) - её координатные функции. Пусть, далее,  - некоторый вектор, а
- некоторый вектор, а 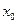 ,
, 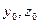 его координаты. Справедливы утверждения, аналогичные теореме о покоорди- натной сходимости:
его координаты. Справедливы утверждения, аналогичные теореме о покоорди- натной сходимости:
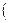

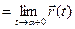
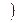
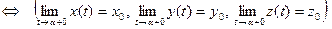 ;
;
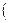

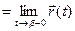
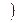
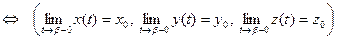 .
.
Доказательства этих утверждений нетрудно скопировать с доказательства тео- ремы о покоординатной сходимости.
Теорема 4. (О связи предела вектор-функции с её односторонними пределами)
Пусть вектор-функция  определена в проколотой окрестности
определена в проколотой окрестности 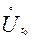 точки t0 , t0
точки t0 , t0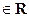 ,, а
,, а - некоторый вектор. Для того, чтобы
- некоторый вектор. Для того, чтобы  являлся пределом
являлся пределом  при
при 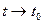 , необходимо и достаточно, чтобы этот вектор был односторонним пределом
, необходимо и достаточно, чтобы этот вектор был односторонним пределом  и при t, стремящемся к t0 слева, и при t, стремящемся к t0 справа:
и при t, стремящемся к t0 слева, и при t, стремящемся к t0 справа:
( =
= 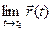 )
) 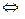 (
( =
= 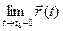 =
= 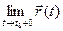 ).
).
►Пусть x (t), y (t) и z (t) - координатные функции вектор-функция  , а
, а 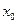 ,
, 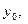
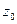 -координаты вектора
-координаты вектора  .
.
Необходимость. Пусть 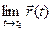 =
= . По теореме о покоординатной сходимости
. По теореме о покоординатной сходимости 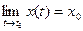 ,
, 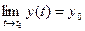 ,
, 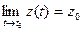 . Отсюда по теореме об односторонних пределах скалярной функции следует:
. Отсюда по теореме об односторонних пределах скалярной функции следует: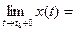
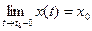 ,
, 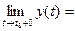
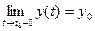 ,
, 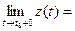
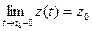 .Отсюда и из сформулированных выше аналогов теоремы о покоординатной сходимости следует:
.Отсюда и из сформулированных выше аналогов теоремы о покоординатной сходимости следует: 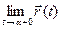
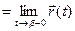 =
= .
.
Доказывая Достаточность следует приведенные выше рассуждения располо- жить в обратном порядке. ◄
1.3. Непрерывность вектор- функции
Определение. Вектор-функцию  называют непрерывной в точке t0 , t0
называют непрерывной в точке t0 , t0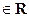 , если она определена в некоторой окрестности этой точки, а её предел при
, если она определена в некоторой окрестности этой точки, а её предел при 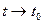 равен
равен 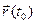 .
.
Теорема 5. (Критерий непрерывности) Пусть вектор-функция  определена в окрестности
определена в окрестности 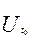 . t0
. t0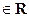 . Для того, чтобы
. Для того, чтобы  была непрерывной в точке t0, необхо- димо и достаточно, чтобы каждая из её координатных функций была непрерывной в этой точке.
была непрерывной в точке t0, необхо- димо и достаточно, чтобы каждая из её координатных функций была непрерывной в этой точке.
► Пусть x (t), y(t) и z (t) - координатные функции вектор-функции  :
: 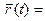
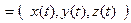 Обозначим: х0 = х (t 0), у0 = y(t 0), z0 = z (t 0); тогда
Обозначим: х0 = х (t 0), у0 = y(t 0), z0 = z (t 0); тогда 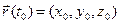 . В силу теоремы о покоординатной сходимости
. В силу теоремы о покоординатной сходимости
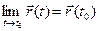
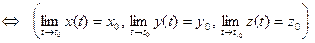 . Отсюда вытекает справедливость утверждений теоремы, так как равенство в левой части есть условие непрерывности вектор-функции в точке t 0, а равенства в правой части – условия непрерывности её координатных функций в той же точке. ◄
. Отсюда вытекает справедливость утверждений теоремы, так как равенство в левой части есть условие непрерывности вектор-функции в точке t 0, а равенства в правой части – условия непрерывности её координатных функций в той же точке. ◄
Разность t – t0 будем называть приращением аргумента t в точке t0 и обозначать через Δ t или h. Заметим: t = t0 + Δ t= t0 + h. Вектор разности  -
-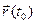 =
= 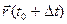 -
-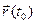 =
= 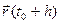 -
-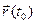 назовем приращением вектор-функции
назовем приращением вектор-функции  в точке t0 и обозначим че- рез Δ
в точке t0 и обозначим че- рез Δ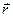 или через Δ
или через Δ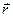 (h), подчеркнув во втором обозначении зависимость этого векто- ра от приращения h = Δ t аргумента t. Заметим:
(h), подчеркнув во втором обозначении зависимость этого векто- ра от приращения h = Δ t аргумента t. Заметим: 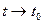
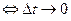 .
.
Теорема 6 (О приращении непрерывной вектор-функции) Пусть вектор-функция  определена в окрестности
определена в окрестности 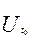 . t0
. t0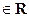 . Для того, чтобы
. Для того, чтобы  была непрерывной в точке t0, необходимо и достаточно, чтобы её приращение было бесконечно малым при
была непрерывной в точке t0, необходимо и достаточно, чтобы её приращение было бесконечно малым при 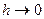 :
: 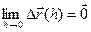 .
.
►Пусть 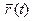
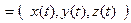 , х0 = х (t 0), у0 = y(t 0), z0 = z (t 0); тогда
, х0 = х (t 0), у0 = y(t 0), z0 = z (t 0); тогда  -
-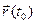 = (x (t)- x (t0), y(t)- y(t0), z (t) - z (t0)), т.е.
= (x (t)- x (t0), y(t)- y(t0), z (t) - z (t0)), т.е.
Δ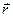 (h) =
(h) = 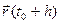 -
-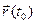 = (x (t0+h)- x (t0), y(t0+h)- y(t0), z (t0+h) - z (t0)) =
= (x (t0+h)- x (t0), y(t0+h)- y(t0), z (t0+h) - z (t0)) =
= (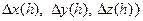
По теореме о покоординатной сходимости
(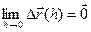 )
)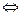 (
(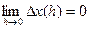 ,
, 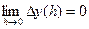 ,
, 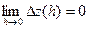 ). Отсюда и из теоремы 5 вытекает справедливость утверждений теоремы 6, так как по теореме о приращении непрерывной скалярной функции равенства
). Отсюда и из теоремы 5 вытекает справедливость утверждений теоремы 6, так как по теореме о приращении непрерывной скалярной функции равенства 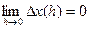 ,
, 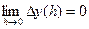 ,
, 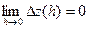 представляют собой необходимые и достаточные условия непрерывности в точке t0 соответствующих координатных функций ◄
представляют собой необходимые и достаточные условия непрерывности в точке t0 соответствующих координатных функций ◄
Определение. Вектор-функцию  назовем непрерывной на интервале (α,β),
назовем непрерывной на интервале (α,β),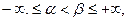 если она непрерывна в каждой его точке. Вектор-функцию
если она непрерывна в каждой его точке. Вектор-функцию  назовём непрерывной на сегменте [α,β],
назовём непрерывной на сегменте [α,β],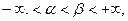 если она непрерывна на интервале (α,β) и, кроме того, непрерывна в точке α справа (т.е.
если она непрерывна на интервале (α,β) и, кроме того, непрерывна в точке α справа (т.е. 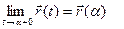 ) и непрерывна в точке β слева (т.е.
) и непрерывна в точке β слева (т.е. 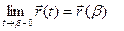 ).
).
 2014-02-09
2014-02-09 5276
5276