Лекция 2. Пример обработки результатов. Функция желательности

Глава 1. Представление результатов экспериментов.

Содержание.

Планирование и обработка результатов экспериментов (дисц.4634).

Лекции

Численные значения могут быть в принципе целочисленными (дискретными, например, число предметов в штуках) и могут быть статистическими, округленными до целых значений или до какого-либо знака после запятой.

Если мы говорим о такой статистической величине, как, например, о длине, которая равна 5 м, то подразумеваем, что величина длины составляет от 4,5 до 5,4. Если мы говорим, что длина равна 5,0 м, то это значит, что ее значение составляет от 4,95 до 5,04 м, если же мы пишем, что длина равна 5,00 м, то это значит, что она составляет от 4,995 до 5,004.

Бессмысленно и безграмотно написать х=5,15 с погрешностью 10%, так как значение 5,15 уже означает, что значение х лежит в пределах от 5,145 до 5,154 или 5,15±0,05 или 0,05/5,15=0,0097≈0,01=1% 5,15±1%.

Если погрешность 10%, или 5,2±0,5, то это значит, что значение х лежит в пределах от 4,7 до 5,7 (или 0,5/5,15=10%).

Бессмысленно и безграмотно написать σ=22,15 с погрешностью 10%, так как значение 22,15 уже означает, что истинное значение σ находится в пределах от 22,15+0,01 до 22,15-0,01 (σ=0,045%) либо, если проводилось округление до 0,05, от 22,15+0,05 до 22,15-0,05 (σ=0,23%). Не совсем правильно написать 20 с погрешностью 10%, это означает, что истинное значение σ лежит в пределах от 20-2 до 20+2, т.е. среднее значение 22,15 выходит за эти пределы.

Правильно написать σ=22 с погрешностью 10%, это будет означать, что σ находится в пределах от 22-2,2 до 22+2,2. Запись в виде σ=22 подразумевает, что истинное значение находится в пределах от 22-1 до 22+1, что указывает на погрешность 5%, несколько лучше фактической погрешности 10%.

Таким образом, допустимо приводить значение без указания погрешности, но так, чтобы подразумеваемая погрешность была такого же порядка, что и фактическая погрешность, но недопустимо приводить значение величины таким образом, чтобы подразумеваемая погрешность отличалась от фактической на несколько порядков (0,045-0,23% вместо фактической 10%.).

В результате экспериментов при определении одного и того же параметра, если отсутствует постоянное влияние внешних факторов, измеряемая величина принимает некоторые случайные значения в определенном диапазоне.

Случайной величиной называется величина, которая принимает определенное значение в допустимых пределах, но само это значение предсказать нельзя. Если исходные факторы одинаковы, то случайная величина может быть различной. Случайная величина может быть непрерывной и дискретной.

Частота появления события (Х) равна частному от деления числа опытов m, когда получается случайная величина Х, на общее число опытов n: m/n. Если n велико, то эта частота стабильна и называется вероятностью события р.

Вероятность того, что наступит хотя бы одно из нескольких несовместимых событий А оавна сумме вероятностей этих событий:

р(А₁+А₂+А₃+...+А_n)=р(А₁)+р(А₂)+ р(А₃)+...+р(А_n)

Вероятность появления всех событий одновременно является произведением вероятностей этих событий:

р(А₁*А₂*А₃*...*А_n)=р(А₁)*р(А₂)*p(А₃)*...*р(А_n)

----------------------------------------------------------------------------------------------

Пример 1. Вероятность безотказной работы прибора зависит от трех узлов, соединенных последовательно. Каждый из них может выйти из строя независимо. Вероятность безотказной работы первого 0,8, второго 0,9 и третьего 0,8. Найти надежность (безотказность) работы прибора в целом. Получаем

р=0,8*0,9*0,8=0,576

---------------------------------------------------------------------------------------------

Сумма вероятностей всех возможных значений случайной величины равна 1 (Sр_i=1), т.е. случайная величина в результате опыта примет одно из своих значений и это есть достоверное событие.

Эта суммарная вероятность распределена определенным образом между отдельными значениями. Дискретную случайную величину можно задать вероятностным рядом, указав вероятность р_i каждого значения х_i.

Соотношение между возможными значениями случайной величины и соответствующими им вероятностями называется законом распределения.

Распределение непрерывной случайной величины характеризуется функцией распределения F(X).

В теории статистических исследований найдено, что нормальная функция распределения равна:

_x

F(x)={1/[s_x (2p)^1/2 ]} ò[exp(-(x-m_x )²/2s_x² ] dx

^-¥

где m_x – среднее арифметическое результатов измерения х

m_x = Σx/N,

N- количество экспериментов, -¥ <x<+¥, σ² – среднеквадратичная погрешность, равная

σ²= Σ(m_x – х)²)/(N-1)

Это распределение наиболее часто встречается на практике.

Нормальное распределение нормированной случайной величины называется стандартным.

_х

F_o(x)={1/[ (2p)^1/2 ]} ò[exp(-(x)²/2 ] dx

^-¥

Для такой величины Р(х₁ <x<x₂ )=F_o(x₂)- F_o(x₁)

Функция F_o(x)-(1/2) называется функцией Лапласа и именно значения этой функции чаще всего приводятся в справочниках в пределах от 0 до 4. При этом Ф(х) изменяется от 0 до 1.

Чтобы от естественных значений х перейти к нормализованным, чтобы было возможно использовать табличные значения Ф(х_о), требуется провести нормализацию:

х_о =(x-m_x)/ s_x

где х_о – нормализованное значение х.

Заметим, что разница F_o(x₂)- F_o(x₁) = Ф(х₀₁) - Ф(х₀₂)

---------------------------------------------------------------------------------------

Вероятность р события случайной величины х<X_m:

р(Х_m<х)=F(x).

Функция F(x) неубывающая. Вероятность

р(х₁<Х<х₂) = F(x₂)-F(x₁)

F(-¥)=0; F(+¥)=1.

Плотность распределения случайной величины

f(x)=dF(x)/dx

Эта величина неотрицательная.

Закон распределения случайной величины (вместо полного распределения) можно охарактеризовать с помощью моментов случайных величин. Начальный момент k-го порядка:

m_k= Sx_i^k p_i

Для непрерывной случайной величины

¥

m=ò xF(x)dx

-¥

Начальный момент первого порядка называется математическим ожиданием (средним арифметическим значением) случайной величины.

Для дискретных случайных величин m₁=Sx_i p_i

Таким образом, первый момент (не центральный) - это математическое ожидание (среднее арифметическое).

Первый центральный момент всегда равен нулю.

Второй центральный момент называется дисперсией (D). Дисперсия случайной величины называется математическим ожиданием квадрата отклонения случайной величины от ее математического ожидания:

_n

D(x)=M[(x-m_x )²] = S((x_i-m_x )²p_i

ⁱ⁼¹

где p_i=n_i/N (N -общее число испытаний, n_i - число испытаний, случающихся с частотой р_i) или,для непрерывной функции распределения,

_¥

D(x) = ò ((x-m_x )²f(x)dx

^-¥

Дисперсию обозначают также D_x. Эта величина равна D_x=s_х² . s_х называют также “стандартом”.

Третий центральный момент, деленный на s_х³ называется коэффициентом асимметрии:

g = m₃/ s_х³

Этот коэффициент выражается через центральные моменты, причем:

m₃ =m₃-3m₁m₂ +2m₁³

Четвертый центральный момент связан с коэффициентом эксцесса (крутости)

t=(m₄/s ⁴)-3

причем, -2< t < +¥. При t>0 - функция распределения более крутая, чем нормальная, при t< 0 - плосковершинная. При t= - 2 она двухвершинная.

Если у случайной величины Х существуют 1-й и 2-й моменты, то можно рассчитать нормированную случайную величину

х_о =(Х-m_x)/s

Для нормированной случайной величины М(х_о)=0; D(x_o )=1.

Существуют зависимости между функциями распределения, соответствующими нормированной х_о и ненормированной Х случайной величиной

f(x)=(1/s_x )f₁(x_o )=(1/s_x)f₁ [(X-m_x )/s_x]

f₁(x_o)= s_xf(x)= s_xf(m_x +s_xx_o)

F(x)=F₁(x_o)= F₁ [(x-m_x )/ s_x]

Ошибки вычислений (измерений)

D_х =S/n^1/2 ; D_s =S/(2N)^1/2;; D_g =(6/N)^1/2 ; D_t =2D_g

Здесь S-выборочная дисперсия.

Доказательство,что распределение нормальное:

g£2D_g и t£2D_t =4D_a

или

|g₁ | £3(D(g₁))^1/2 и t £=5(D(t))^1/2

где

D(g₁ )=6(n-1)/[(n+2)(n+3)];

D(t)=24n(n-2)(n-3)/[(n+1)² (n+3)(n+5)]

Точность вычислений

e=(D(х_ср)/х_ср ).100%

Графики функций распределения с ненулевыми коэффициентами асимметрии g₁ и эксцесса t показаны на рис. 1. Если g₁ >0,то вершина кривой сдвинута влево. Если g₁<0, то вправо. Если t>0, то кривая ненормально узкая. Если t<0, то кривая двугорбая.

Если меры косости и крутости не превышают свои основные ошибки более чем в 3-4 раза, то это является основанием для заключения о нормальном законе распределения.

Результаты экспериментов, перед их представлением, опубликованием, требуют анализа для оценки погрешности.

Для получения достаточно надежных экспериментальных данных требуется, чтобы эти результаты были получены многократно, например N раз. В этом случае за результат принимают среднее арифметическое значение Хср=ΣХ/N Однако это значение будет верным только в том случае, если получаемые экспериментальные значения будут случайными и их распределение будет подчиняться закону Гаусса – в частности распределение Х по значениям будет симметрично.(См. рис.1).

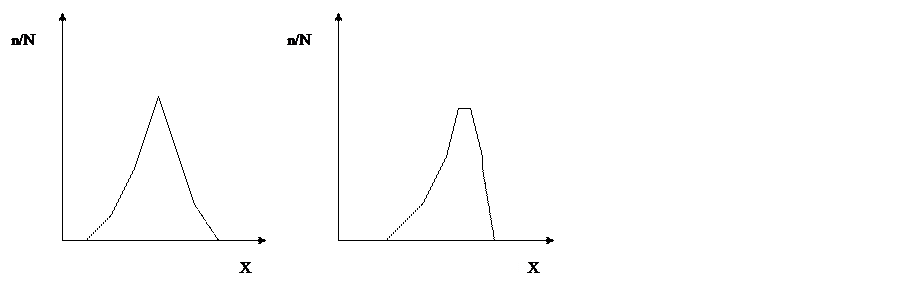
Рис.1. Нормальное (и симметричное) распределение случайной величины.

Рис.2. Асимметричное распределение случайной величины.

Если же кривая распределения не симметрична (См. рис.2), то можно попытаться выбрать такую функцию Ф(Х), чтобы получить симметричный вид распределения, тогда среднее арифметическое значение уже этой функции Ф(Х) можно будет рассматривать как представительное. Одним из вариантов получения симметричного распределения является логарифмическое распределение Ф(lgХ).

Представляемое экспериментальное значение имеет определенную погрешность. Стандартное значение дисперсии σ =Σ(Х-Хср)²/(N-1) представляет собой значение, характеризующее интервал, в котором искомое значение Х с вероятностью 72% находится в диапазоне от Х+σ до Х-σ. Однако достаточно надежным считаются значение, вероятность правильности которого составляет, например, 95%, от Х- ε до Х+ε. Значение ε связано с σ соотношением включающем критерий Стьюдента t:

ε=σt/(N)^0,5.

Значение t найдем из Таблицы 1, где приведены значения t при разном количестве экспериментов N c разной степенью вероятности.

Таблица 1. Критерий Стьюдента t: Значения t при данном числе испытаний N и заданной величине доверительной вероятности (уровне значимости) Р.

N-1	Р= 0,90	P= =0,95	P= =0,98	Р= 0,99	N-1	Р= 0,90	P= =0,95	P= =0,98	Р= =0,99
	6,31	12,704	31,821	63,7		1,80	2,201	2,718	3,11
	2,92	4,303	6,965	9,93		1,78	2,179	2,681	3,06
	2,35	3,182	4,541	5,84		1,77	2,160	2,650	3,01
	2,13	2,778	3,747	4,60		1,76	2,145	2,624	2,98
	2,02	2,571	3,365	4,03		1,75	2,131	2,602	2,95
	1,94	2,447	3,143	3,71		1,75	2,120	2,583	2,92
	1,90	2,365	2,998	3,50		1,74	2,110	2,567	2,90
	1,86	2,306	2,896	3,36		1,73	2,086	2,528	2,85
	1,83	2,262	2,821	3,25		1,71	2,060	2,485	2,79
	1,81	2,288	2,764	3,17		1,70	2,042	2,457	2,75

Таким образом, для повышения точности значения Х (т.е. снижения ε) требуется увеличение количества экспериментов N.

Зачастую нет необходимости указывать параметры погрешности σ или ε, можно просто привести цифровое значение, например предел прочности при растяжении f = 22 кг/мм². Если именно так приведено это значение, то это значит, что f лежит в пределах от 21,5 до 22,4 или σ лежит в пределах от 22-0,5 до 22+0,5 или ε ≈ 0,5. Эта величина составляет 0,5/22*100%= 2,3%, что очень неплохая точность. Обычно прочностные показатели определяются с погрешностью до +-15%. Если же вы хотите показать, что f определено с более высокой погрешностью, то представляемое число следует округлить до 20, или 2.10¹, что указывает на то, что действительная величина лежит в пределах от 15 до 25 или от 20-5 до 20+5, или ε=5 или ε=5/20≈25%.

Пример 2.

Решение задач о погрешностях.

Найти вероятность того, что абсолютное отклонение Dх= êx-m_х êне превзойдет заданного числа e

Р(Dх£e)=З(m_x-e £ m_x+e)

Для нормированной случайной функции

P(-e£ x_o £ e)=Ф(e)-Ф(-e)=2Ф(e)

Для случайной величины, имеющей нормальное распределение с параметрами m_x и s_х

Р(Dх£e)=Р(Dх_о£e/s_х)=2Ф(e/s_х)

Обозначив k=e/s_х получим функцию Лапласа Ф:

Р(Dх£ks_х)= 2Ф(k)

P(Dх£s_х)=2Ф(1)=0,6826

P(Dх£2s_х)=2Ф(2)=0,9544

P(Dх£3s_х)=2Ф(3)=0,9973

Последняя величина указывает на практически невозможное событие.

Пример 3. Толщину керамической плитки h можно считать случайной величиной, распределенной по нормальному закону с s_х =0,3 мм. Какова вероятность брака, при котором Dh³0,5 мм?

Вероятность противного события: Р(Dh£0,5)=2Ф(0,5/0,3)=0,905

Отсюда Р(Dh³0,5)=1-0,905=0,095.

Определение параметров функции распределения.

Берем выборку (n значений) из генеральной совокупности (т.е. все

допустимые значения случайной величины. Весь диапазон изменения случайной величины делим на k интервалов. Рекомендуемое значение k:

k=1+3,2lg(n)

Длина интервала h=(X_макс -X_мин)/k. Подсчитаем число элементов

выборки,попадающих в отдельный интервал n. Относительная частота попадания случайной величины в i-й интервал Р_i =n_i/n. Все точки, попавшие в i-й интервал относят к середине интервала

X_i^* =(X_i-1 +X_i)/2

Строят диаграмму-график, по оси абсцисс откладывают значения

X_i ^* и по оси ординат значения n_i. Полученные точки соединяют между собой, таким образом получают экспериментальную кривую распределения - “полигон”. Это дифференциальная кривая распределения. Интегральную кривую распределения получают, откладывая по оси ординат суммы n_i всех точек, находящихся слева (со стороны более низких значений X).

Оценка математического ожидания и дисперсии. Для нормального

распределения получают среднее арифметическое значение X_cp =S X_i /n и выборочную дисперсию S²=S(X_i -X_cp)² /n. Величина S “смещена”.

Для получения несмещенной оценки ее умножают на n/(n-1). Тогда получаем:

S² =S(X_i -X_cp)²/(n-1). Удобная для программирования формула:

S²=│(SX_i ² -(SX_i)²)/n│

Ошибки измерений.

Ошибки бывают грубые, систематические и случайные. Случайные

ошибки - остающиеся после устранения грубых и систематических, они вызываются большим количеством таких факторов, эффекты действия которых столь незначительны, что их нельзя выделить в отдельности.

Если результатов испытаний много, то значения X частичной совокупности из n значений, полученных путем независимых испытаний, распределяется нормально со средним значением X_ср и дисперсией s². Нормированное отклонение (X_ср -X_i)/sn^-1/2) распределяется нормально со средним значением равным нулю и дисперсией, равной единице. Однако при исследованиях дисперсия s² почти всегда остается

неизвестной и мы не можем произвести нормирование. Отклонение среднего значения частичной (выборочной) совокупности от среднего значения нормальной общейокупности, нормированное с помощью S² (несмещенная оценка выборочной дисперсии) обозначается t:

t=((X_cp - m_x)/S) n^1/2

Функция распределения t имеет сложный вид, в нее входит число степеней свободы n. Интегрируя f(t) от - ¥ до t найдем вероятность S_n(t) случайных значений t_o меньших, чем заданное t:

S_n(t)=Р[t_о <t]

Распределение S(t) - распределение Стьюдента или t-распределение.Это распределение используется для ответа на вопрос, является ли значимым наблюдаемое значение (для оценки средних значений).

Результаты испытаний на электрическую прочность
			(U-Ucp)^2
		5,1	26,01
		0,1	0,01
		-1,9	3,61
		3,1	9,61
		2,1	4,41
		2,1	4,41
		4,1	16,81
		1,1	1,21
		0,1	0,01
		-0,9	0,81
summa			66,9
srednee	22,9
σ^2=	=66,9/ (10-1)	7,433333
σ=		2,726414
ε=	2,262*S/N^0,5
	1,950224
U=	22,9+-1,95
U≈	23 ± 2	±

В качестве примера рассмотрим обработку результатов при определении электрической прочности. В целях получения достоверных результатов при значительном разбросе данных проводят ряд повторных (иногда десятки) испытаний одного и того же материала.

Пусть при одних и тех же условиях проведено N пробоев, пробивные напряжения при этом оказались равны U1,U2…Ui, Ux. Среднее значение пробивного напряжения – сумма всех значений Ui, деленная на число пробоев

Ucp= ΣUi/N

Разброс пробивных напряжений Ui относительно среднего значения Ucp характеризуется среднеквадратичным отклонением σ

σ= [Σ(Ui-Ucp)²/(N-1)]^1/2

Вероятность пробоя одного и того же материала при неизменных условиях и при многократных испытаниях на партии образцов определяют путем построения дифференциальной и интегральной кривых вероятности в функции напряжения. Пусть все необходимые значения пробивного напряжения находятся в определенном диапазоне. Разобьем это диапазон на ряд небольших одинаковых интервалов ΔU и найдем число пробоев n для каждого интервала. Таким образом, первому интервалу напряжений будет соответствовать n1 пробоев, второму n2 -число пробоев, k–тому число пробоев n_k и т.д. Пусть таких интервалов оказалось m, очевидно m<N. Сумма всех значений n_k должна равняться общему числу пробоев.

Σn_k=N

При большом числе пробоев вместо трудоемкого определения среднего значения пробивного напряжения для всех N пробоев довольствуются приближенным средним статистическим пробивным напряжением Ucp.cт., Оно определяется следующим образом. Для каждого интервала k напряжений находят произведение p_k*U_k, где р_k=(n_k/N)*100. Сумма этих произведений, деленная на 100 и даст значение Ucp.cт:

Ucp.cт=(1/100)Σp_kU_k

Эта величина близка к Ucp, но не равна ей, так как в пределах интервала усреднялись значения напряжения. При достаточно малых интервалах

Ucp.cт ≈ Uср

Вероятность р того, что пробой произойдет при напряжении U, соответствующем интервалу определяется в % отношением

100(n_k/N)=p_k

Можно построить ступенчатый график p(U) выражающий зависимость р от напряжения U. Сумма всех значений p_k равняется

Σp_k=(100/N)Σn_k=(100/N)N = 100%

Откладывая по оси ординат р, а по оси абсцисс напряжение при пробое для каждого интервала, получают ступенчатый график (рис.) называемый гистограммой. Плавная кривая, проведенная через средние точки графика, представляет собой дифференциальную кривую вероятности.

Заметим, что при увеличении числа наблюдений график р(U) приближается в плавной кривой, симметрично расположенной около центральной ординаты. Уравнение такой кривой (для рассматриваемого процесса пробоя однородных диэлектриков) имеет вид:

p(U)=1/[σ(2π)^1/2]exp[-(U-Ucp)/(2σ²)]

Эта кривая выражает так называемый нормальный закон распределения вероятностей Гаусса.

Для построения интегральной кривой найдем соответствующее каждому интервалу k число пробоев М (в процентах от общего числа пробоев N), т.е. число образцов, пробитых при напряжении U_k и при более низких значениях напряжения. Нарастающая зависимость М(U) носит название интегральной кривой.

Дифференциальная и интегральная кривые вероятности играют важную роль не только при определении электрической прочности материалов, но также при оценке других их свойств.

Доверительный интервал. Вероятность того, что абсолютное значение отклонения какой-либо величины (пробивного напряжения) от среднего значения этой величины

│Uk-Ucp│

не превышает некоторого значения u, выражается функцией Лапласа

Ф(z)=Ф(u /(σ^1/2))

Где σ – среднеквадратичной отклонение. Эта функция представляет собой определенный интеграл вида

z

Ф(z)=(2/π)∫еxp(-t²)dt

Ee значения даются в виде таблиц в справочниках.

Рассмотрим значения вероятности отклонения для некоторых частных случаев.

1) u=σ. Тогда вероятность отклонения при │Uk-Ucp│<= σ,будет равна Ф=0,68.

2) u=1,5σ. Ф=0,866 ≈ 0,9.

3) u=2σ. Ф=0,954.

Таким образом, если на гистограмме отложить влево и вправо от средней величины 2σ, то количество пробоев в этом интервале составляет 95% от общего числа пробоев. Зачастую довольствуются значением 1,5σ, считают, что за этим интервалом измеряемые величины встречаются редко, в виде единичных случаев.

Коэффициентом вариации называют отношение

k=σ/Ucp*100%

Считают, что материалы с k ≤15% являются однородными, а при большей величине k - недостаточно однородными.

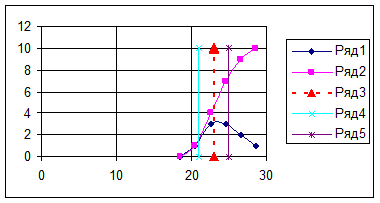
Рис.2. Пример интегральной (ряд 2) и дифференциальной (ряд 1) функций распределения. По оси абсцисс нанесены значения электрической прочности. По оси ординат нанесены величины пропорциональные плотности вероятности. Показано среднее значение (ряд 3), совпадающее с наивероятнейшим значением.

Пороговое пробивное напряжение.

Определение наиболее низкого пробивного напряжения, при котором (как и при более высоких значениях) пробивается значительное количество образцов (или происходит большое число пробоев) имеет важное значение для конструирования электроизоляционных конструкций и их расчетов. Очевидно, при многократных испытаниях всегда будут наблюдаться единичные пробои, отвечающие некоторому значению U_пр.мин; вероятность появления таких пробоев ничтожно мала, и едва ли можно эту величину, U_пр.мин положить в основу оценки электрической прочности материала. Иногда в качестве критерия используют величину среднего пробивного напряжения U_ср≈ U_ср.ст, но при этом следует учитывать, что около половины пробоев будет наблюдаться при более низких (по с сравнению с U_ср) пробивных напряжениях.

Более обоснованным является подход к оценке электрической прочности, основанный на разумной минимально допустимой (пороговой) вероятности пробоя М_пор, равной, например, 5-10%. Пробивное напряжение, U_пор, при котором (как и при более низких) пробьется М_пор процентов общего числа образцов, называют пороговым пробивным напряжением при заданной минимально допустимой вероятности. Нетрудно заметить, что

U_мин <U_пор< U_ср

Для получения порогового напряжения U_пор откладывают по вертикальной оси М значение интегральной вероятности М_пор и, проведя горизонтальную прямую до пересечения с интегральной кривой, находят U_пор.

Проследим на численном примере методику статистической обработки результатов испытаний. Определение электрической прочности одного из материалов показало, что значение U_пр лежит в пределах от 27 до 33 кВ. Весь диапазон напряжений можно разбить на интервалы по 0,4 кВ, причем таких интервалов оказалось 15, а вероятность р числа пробоев для отдельных интервалов колебалась от 0,3 до 16%. По этим данным построим дифференциальную кривую вероятности, которая оказалась близкой к нормальному закону распределения. Складывая значения р для каждого интервала со значениями р в предыдущих интервалах, получают значения М, по которым построена интегральная кривая распределения. Пусть М_пор=5%; отложив это значение по оси М и проведя горизонтальную прямую до пересечения с интегральной кривой, находит U_пор =28,2 кВ.

Интересно отметить, что в данном случае среднестатистическое пробивное напряжение составляет

U_ср.ст=30,24 кВ.

Среднеквадратичное отклонение равняется σ=0,676 кВ.

Коэффициент вариации составляет величину

k_вар=2,24%.

Таким образом, материал, подвергнутый испытаниям, относится к

материалам первой группы однородности («материал однородный»).