Определение 7. Непрерывная случайная величина имеет нормальное распределение, с двумя параметрами a, s, если
 , s>0. (5)
, s>0. (5)
Тот факт, что случайная величина имеет нормальное распределение, будем кратко записывать в виде Х ~ N (a; s).
Покажем, что p (x) – плотность
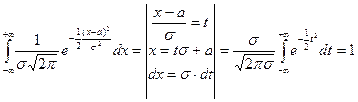 (показано в лекции 6).
(показано в лекции 6).
График плотности нормального распределения (рис. 3) называют нормальной кривой (кривой Гаусса).
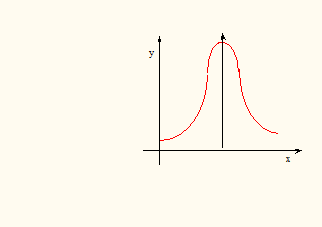
Рис.3
Плотность распределения симметрична относительно прямой х = a. Если х ® ¥, то р (х) ® 0. При уменьшении s график «стягивается» к оси симметрии х = a.
Нормальное распределение играет особую роль в теории вероятностей и ее приложениях. Это связано с тем, что в соответствии с центральной предельной теоремой теории вероятностей при выполнении определенных условий сумма большого числа случайных величин имеет «примерно» нормальное распределение.
Так как 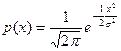 – плотность нормального закона распределения с параметрами а = 0 и s =1, то функция
– плотность нормального закона распределения с параметрами а = 0 и s =1, то функция  = Ф (х), с помощью которой вычисляется вероятность
= Ф (х), с помощью которой вычисляется вероятность 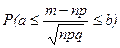 , является функцией распределения нормального распределения с параметрами а = 0 и s =1.
, является функцией распределения нормального распределения с параметрами а = 0 и s =1.
Функцию распределения случайной величины Х с произвольными параметрами а, s можно выразить через Ф (х) – функцию распределения нормальной случайной величины с параметрами а = 0 и s =1.
Пусть Х ~ N (a;s), тогда
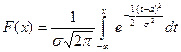 . (6)
. (6)
Сделаем замену переменных под знаком интеграла 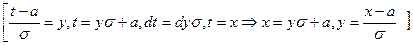 , получим
, получим
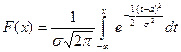 =
=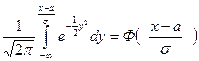
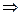
F (x) = 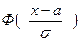 . (7)
. (7)
В практических приложениях теории вероятностей часто требуется найти вероятность того, что случайная величина примет значение из заданного отрезка 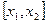 . В соответствии с формулой (7) эту вероятность можно найти по табличным значениям функции Лапласа
. В соответствии с формулой (7) эту вероятность можно найти по табличным значениям функции Лапласа
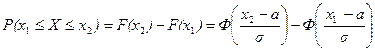 . (8)
. (8)
Найдем медиану нормальной случайной величины Х ~ N (a; s). Так как плотность распределения р(х) симметрична относительно оси х = а, то
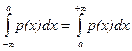
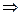
 р (х < a) = p (x > a) = 0,5.
р (х < a) = p (x > a) = 0,5.
Следовательно, медиана нормальной случайной величины совпадает с параметром а:
Х 0,5 = а.
Задача 1. Поезда в метро идут с интервалом в 2 мин. Пассажир выходит на платформу в некоторый момент времени. Время Х, в течение которого ему придется ждать поезд, представляет собой случайную величину, распределенную с равномерной плотностью на участке (0, 2) мин. Найти вероятность того, что пассажиру придется ждать ближайший поезд не более 0,5 мин.
Решение. Очевидно, что p(x) = 1/2. Тогда, Р0,5 = Р( 1,5 <X< 2 ) = 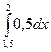 = 0,25
= 0,25
Задача 2. Волжский автомобильный завод запускает в производство новый двигатель. Предполагается, что средняя длина пробега автомобиля с новым двигателем – 160 тыс. км, со стандартным отклонением – σ = 30 тыс.км. Чему равна вероятность, что до первого ремонта число км. пробега автомобиля будет находиться в пределах от 100 тыс. км. до 180 тыс. км.
Решение. Р(100000< X < 180000) = 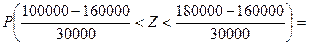 Ф(2/3)–Ф(–2) = 0,2454 + 0,4772 = 0,7226.
Ф(2/3)–Ф(–2) = 0,2454 + 0,4772 = 0,7226.
 2014-02-18
2014-02-18 938
938








