4.1. а) 4 %
б) 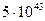
4.2. 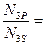 1.4×
1.4×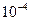
4.3. а) 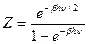 .
.
На основании того, что 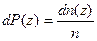 , из (7.2) получается выражение для пространственной концентрации частиц
, из (7.2) получается выражение для пространственной концентрации частиц 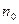 как функции от высоты z:
как функции от высоты z:
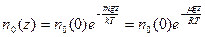 , (7.3)
, (7.3)
где 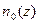 – концентрация частиц на высоте z,
– концентрация частиц на высоте z, 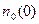 -концентрация на высоте, где потенциальная энергия равна нулю,
-концентрация на высоте, где потенциальная энергия равна нулю, 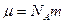 – молярная масса газа, R=8,314 Дж/(моль×К) (универсальная газовая постоянная). Выражение для
– молярная масса газа, R=8,314 Дж/(моль×К) (универсальная газовая постоянная). Выражение для 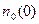 может быть получено из условия сохранения количества частиц в газовом столбе высотой Н и площадью сечения S =1
может быть получено из условия сохранения количества частиц в газовом столбе высотой Н и площадью сечения S =1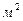 :
:
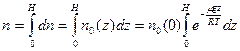 ,
,
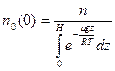 . (7.4)
. (7.4)
В поле центробежных сил, например, во вращающейся с угловой скоростью 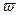 центрифуге,
центрифуге, 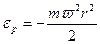 – потенциальная энергия молекулы зависит от ее удаленности r от оси вращения. В этом случае пространственная концентрация определяется следующим образом:
– потенциальная энергия молекулы зависит от ее удаленности r от оси вращения. В этом случае пространственная концентрация определяется следующим образом:
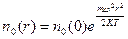 , (7.5)
, (7.5)
где 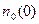 – концентрация частиц на оси вращающегося цилиндра. Значение этой величины можно получить из условия сохранения полного числа частиц в объеме
– концентрация частиц на оси вращающегося цилиндра. Значение этой величины можно получить из условия сохранения полного числа частиц в объеме 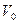 цилиндра радиуса R и высоты H.
цилиндра радиуса R и высоты H.
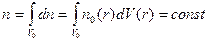 . (7.6)
. (7.6)

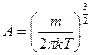 (5.2)
(5.2)
При решении некоторых задач удобно пользоваться распределением Максвелла по отдельным компонентам скоростей:
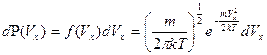 (5.3)
(5.3)
– это вероятность того, что значение компоненты скорости 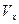 частицы лежит в интервале от
частицы лежит в интервале от 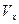 до
до 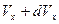 . Аналогичные выражения справедливы для вероятностей
. Аналогичные выражения справедливы для вероятностей 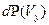 и
и 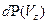 . Примерный вид плотности вероятности
. Примерный вид плотности вероятности 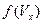 приведен на рис.5.1.
приведен на рис.5.1.
В сферической системе координат распределение Максвелла, в случае изотропного пространства, имеет следующий вид:

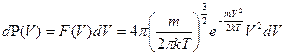 . (5.4)
. (5.4)
Оно отвечает на вопрос какова вероятность того, что абсолютная скорость частицы лежит в интервале от 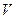 до
до 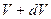 , а также на вопрос, сколько частиц
, а также на вопрос, сколько частиц 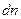 из
из 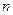 имеют абсолютную скорость в заданном интервале:
имеют абсолютную скорость в заданном интервале:
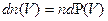 . (5.5)
. (5.5)
Следует отметить, что 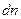 и
и 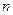 – очень большие числа, но
– очень большие числа, но 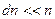 . Соответственно, доля частиц, имеющих абсолютную скорость в интервале от
. Соответственно, доля частиц, имеющих абсолютную скорость в интервале от 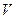 до
до 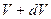 , равна
, равна
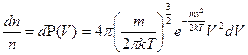 . (5.6)
. (5.6)
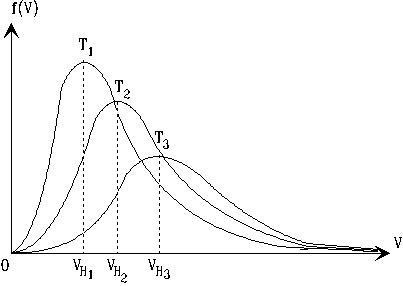
На рис.5.2 приведен примерный вид плотностей вероятности распределения Максвелла для различных температур. Здесь же
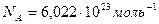 (постоянная Авогадро),
(постоянная Авогадро), 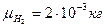 , T =300K, V =500 м/с,
, T =300K, V =500 м/с, 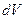 =2 м/с, R =8,31
=2 м/с, R =8,31 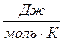 , получаем
, получаем 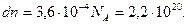
5.2. Значения всех величин равны нулю.
5.3. 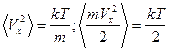 .
.
5.4. 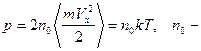 концентрация идеального газа.
концентрация идеального газа.
5.5. a) 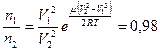 , б)
, б) 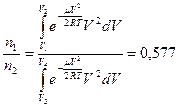 .
.
5.6. 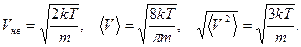
5.7. 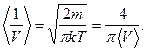
5.8. 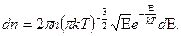
5.9. 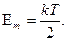
5.10. 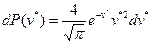
5.11. 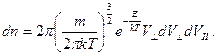
Рис.5.2
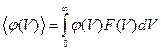 . (5.8)
. (5.8)
Среднее значение параметра, зависящего от одной компоненты скорости, вычисляется по формуле
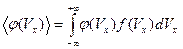 . (5.9)
. (5.9)
В случае, когда параметр зависит от двух или трех компонент скорости, для его усреднения следует использовать распределение (5.1).
Характерными скоростями распределения Максвелла принято называть три величины:
1. Наивероятнейшая скорость - 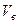 .
.
2. Средняя скорость - 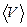 .
.
3. Средняя квадратичная скорость - 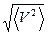 .
.
 |
З а д а ч и
|
|
5.2. Исходя из распределения Максвелла, найти следующие величины:
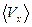 ,
, 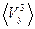 ,
,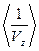 .
.
5.3. Получить выражение для среднего квадрата x-компоненты скорости молекулы газа. Найти среднюю кинетическую энергию, приходящуюся на одну степень свободы поступательного движения молекулы газа.
5.4. Используя распределение Максвелла по одной компоненте скорости, получить выражение для давления на стенку сосуда.
5.5. Найти отношение числа молекул водорода 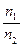 , если температура водорода 300°С: а) число частиц
, если температура водорода 300°С: а) число частиц 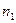 имеют скорости от 3000 м/c до 3010 м/с, а
имеют скорости от 3000 м/c до 3010 м/с, а 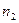 - в пределах от 1500 м/c до 1510 м/c; б) для
- в пределах от 1500 м/c до 1510 м/c; б) для 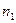 интервал скоростей от 3000 м/с до 4000 м/с, для
интервал скоростей от 3000 м/с до 4000 м/с, для 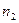 – от 2000 м/c до 3000 м/c.
– от 2000 м/c до 3000 м/c.
5.6. Получить выражения для трех характерных скоростей распределения Максвелла.
5.7. Найти среднее значение обратной величины скорости молекулы в газе.
5.8. Написать выражение для среднего числа 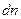 молекул газа, кинетические энергии которых заключены между
молекул газа, кинетические энергии которых заключены между 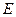 и
и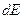 .
.
 2014-02-24
2014-02-24 407
407








