Стохастическая модель стоимости товаров в торговых центрах

КОНТРОЛЬНЫЕ ВОПРОСЫ 8

Задача оптимального размещения предприятий

Задача о выборе геометрических размеров бака заданного объема

Пусть требуется выбрать геометрические размеры цилиндрического бака заданного объема V, из условия минимального расхода материала на его изготовление. Введем вектор проектных решений 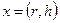, где 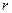– радиус, h – высота бака. Будем считать, что бак изготовлен сваркой из трех деталей (рис. 5.1).

В этом случае расход материала при произвольном векторе решения x равен площади поверхности бака S

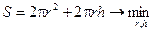. (5.1)

Условие того, что бак должен иметь заданное значение объема:

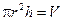. (5.2)

На компоненты вектора 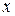нужно наложить ограничения

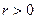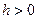, . (5.3)

Таким образом, выражения (5.1) - (5.3) описывают нелинейную однокритериальную модель задачи формирования оптимальных решений. Отметим, что данная модель была построена с использованием закономерностей элементарной геометрии. Если потребовать, чтобы бак имел минимальную трудоемкость его изготовления, а также предположить, что трудоемкость изготовления крышек и боковой стенки пренебрежимо малы (штамповка), то затраты времени на изготовление бака будут пропорциональны длине свариваемых швов.

, (5.4)

где t – затраты времени на сварку единицы длины шва. Выражения (5.4), (5.2), (5.3) также представляют собой однокритериальную нелинейную модель. Выражения (5.1), (5.4), (5.2), (5.3) описывают двухкритериальную нелинейную модель формирования оптимального проектного решения на бак.

Как было сказано выше, нелинейные модели в некоторых частных случаях допускают получение аналитического решения, то есть решения в виде формул. Построим аналитическое решение задачи (5.4), (5.2), (5.3), отбросив условие (5.3). Будем определять оптимальные значения r и h с помощью метода Лагранжа, применяемого в случае, когда все ограничения вида (3.2) имеют вид равенств:

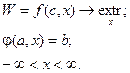
Функция Лагранжа имеет следующий вид:

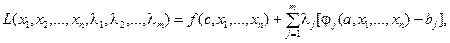
где l₁, l₂, …, l _m – неопределенные множители Лагранжа.

Точки экстремума этой функции определяются из решения системы уравнений вида

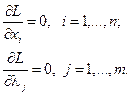
Решая эту систему, получим решение вида

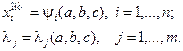
Запишем функцию Лагранжа для задачи (5.4), (5.2):

,

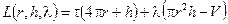Используя необходимое условие экстремума функции L, получаем систему уравнений для определения неизвестных h, 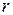и l:

.

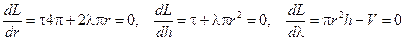Оптимальное проектное решение имеет вид: , .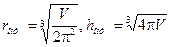

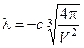Оптимальное решение не зависит от квалификации сварщика (t), причем оптимальная высота бака равна длине его окружности:

.

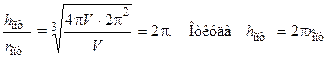Пусть имеется два пункта потребления некоторого товара, на расстоянии 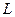друг от друга. Между этими пунктами требуется разместить предприятие, обеспечивающее выпуск 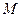единиц товара. Будем считать, что пункты потребления должны использовать весь товар в объеме 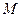. Известно, что стоимость перевозки единицы товара пропорциональна расстоянию от предприятия до пункта потребления.

Требуется определить точку размещения предприятия и объемы поставок товара каждому потребителю, так чтобы суммарные транспортные расходы были минимальными (рис. 5.2).

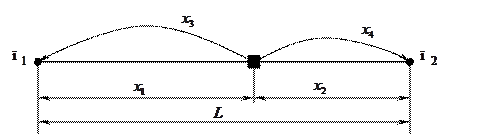
Рис. 5.2

Введенные переменные должны удовлетворять условиям:

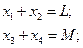(5.5)

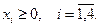(5.6)

Построим целевую функцию задачи. Стоимость перевозок единиц товара потребителям записывается как:

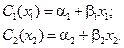(5.7)

Здесь 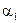, 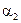– постоянные части стоимости перевозки единицы товара (например, з/п шофера, не зависящая от расстояния). Тогда стоимость перевозки всего объема произведенного товара вычисляется по формуле:

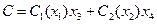. (5.8)

Подставляя сюда выражения (5.7) получаем окончательный вид целевой функции:

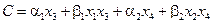. (5.9)

Получим нелинейную однокритериальную модель, которая описывается выражениями (5.9), (5.5), (5.6).

Решим поставленную задачу методом Лагранжа.

Функция Лагранжа имеет вид:

.

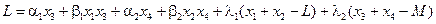Возьмем частные производные по х ₁, х ₂, х ₃, х ₄, l₁, l₂:

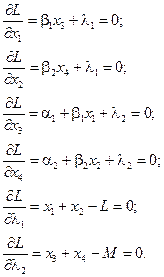
Решая полученную систему уравнений, получим:

, , , .

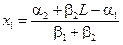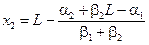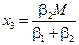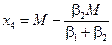1. Сформулируйте задачу о выборе геометрических размеров бака заданного объема.

2. Приведите ММ минимизации расхода материала в задаче о баке.

3. Приведите ММ минимизации трудоемкости изготовления бака.

4. В чем заключается метод Лагранжа при построении аналитического решения ЗПР?

5. Приведите общий вид функции Лагранжа.

6. Как найти точки экстремума функции Лагранжа?

7. Запишите функцию Лагранжа для однокритериальной задачи о баке.

8. Запишите функцию Лагранжа для двухкритериальной задачи о баке.

9. Сформулируйте задачу оптимального размещения предприятий.

10. Приведите ММ стоимости всего объема произведенного товара в задаче оптимального размещения предприятий.

11. Каким методом решена задача оптимального размещения предприятий?

12. Почему в задаче оптимального размещения предприятий возможно использование метода Лагранжа?

13. Приведите функцию Лагранжа для решения задачи оптимального размещения предприятий.

5.3. Стохастическая модель выбора оптимальной производственной
программы

Лекция 9

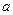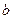Все рассмотренные выше задачи относились к детерминированным задачам принятия решений, то есть к задачам в которых , и 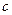были достоверно известны до решения задач. Существует класс задач, в которых эти параметры описываются случайными векторами. В этом случае соответствующие ММ относятся к классу стохастических задач. Рассмотрим пример одной из таких задач.

Рассмотренная выше классическая модель выбора оптимальной программы:

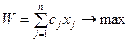; (5.10)

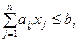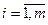, ; (5.11)

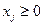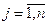, (5.12)

относится к классу детерминированных моделей, так как предполагалось, что все параметры 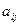, 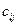и 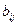не случайные величины. В реальности за счет нестабильности в экономике и действия в производственных процессах всевозможных факторов эти параметры могут рассматриваться как случайные величины. В этом случае оптимальный выбор производственной программы необходимо осуществить с помощью стохастических моделей.

Рассмотрим случаи, когда прибыль от реализации единицы продукции, запасы сырья и материалов являются случайными величинами.

Пусть значения прибыли от реализации j -й продукции 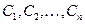являются случайными величинами. В этом случае суммарная прибыль от реализации продукции:

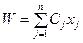. (5.13)

Максимизировать это выражение нельзя, так как в этом случае компоненты вектора решения х будут являться случайными величинами. Отметим, что при использовании любых стохастических моделей обязательно получение детерминированных компонент 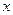, учитывающих тот факт, что в задаче имеются случайные параметры. Будем считать, что из обработанной статистики нам известны математические ожидания и дисперсии случайных величин.

, , .

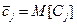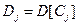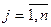Тогда критерий максимума средней прибыли записывается так:

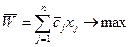. (5.14)

Здесь было использовано выражение (5.13), в котором все случайные величины были заменены их математическими ожиданиями (свойство линейной комбинации случайных величин). Теперь вид ММ определяют выражения (5.14), (5.11), (5.12).

Можно сформулировать задачу выбора оптимального вектора 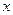, обеспечивающего минимальную дисперсию суммарной прибыли (5.13). Для этого используем следующее правило теории вероятности. Пусть случайная величина 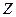вычисляется на основе коррелированных случайных величин 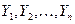как сумма линейной комбинации

,

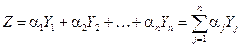где 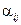– неслучайные константы.

Тогда дисперсия случайной величины 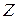вычисляется так:

,

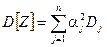где 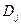– дисперсия случайной величины Y_j.

Применим это правило к выражению (5.13), где роль неслучайных параметров играют компоненты вектора 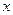, получаем:

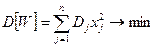(5.15)

Таким образом, при случайных значениях прибыли можно решать двухкритериальную задачу (5.15), (5.14), (5.11), (5.12), обеспечивающую максимум средней прибыли и минимум ее дисперсии.

Рассмотрим случай, когда случайным является объем ресурсов входящих в условие (5.11). Пусть 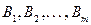– случайные величины, описывающие эти объемы. В этом случае условие (5.11) становится случайным неравенством вида:

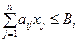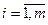, (5.16)

Будем считать, что каждая случайная величина описывается ее функцией распределения:

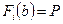
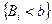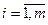, (5.17)

Потребуем, чтобы неравенство (5.16) выполнялись с вероятностью близкой к единице. Это требование можно записать в виде

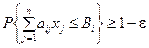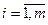, (5.18)

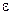– достаточно малая величина, которая в практических задачах принимает значения 0,01; 0,05; 0,1. Из выражения (5.17) следует, что вероятность

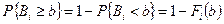. (5.19)

С учетом этого левую часть выражения (5.18) представим в виде

.

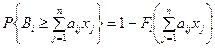Подставим полученное выражение в неравенство (5.18), получим

.

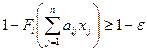Приводя подобные члены и изменяя вид неравенств, получаем:

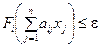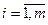, . (5.20)

Таким образом, выражения (5.10), (5.20), (5.12) представляют собой стохастическую однокритериальную модель оптимальной производственной программы при случайной доступности ресурсов.

Рассмотрим пример, когда все случайные величины 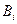распределены по равномерному закону в соответствующих интервалах (рис. 5.3).

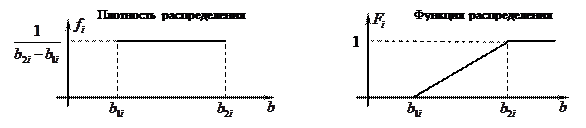
Рис. 5.3

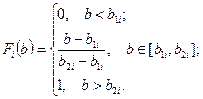
С учетом этого неравенство (5.18) примет вид:

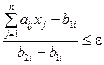
Проведя преобразования, имеем:

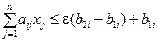
Эти линейные неравенства заменяют неравенства вида (5.16) в конкретных задачах ПР.

Построим конкретный вид неравенства (5.16) для случая, когда случайная величина 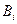распределена по показательному закону с функцией распределения вида:

.

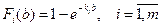Согласно (5.20) 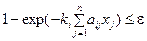. Перенесем «единицу» в правую часть и прологарифмируем обе части неравенства, получим: 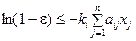. Отсюда:

.

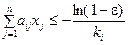Будем считать, что некоторому ТЦ предоставлена возможность варьирования розничной ценой на некоторый товар.

Обозначим через 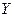случайную величину, описывающую спрос на рассматриваемый товар за некоторый промежуток времени (день, неделя, месяц). Доход от реализации товара за этот промежуток времени будет описываться случайной величиной

,

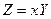(5.21)

где х – розничная цена рассматриваемого товара.

Сформулируем задачу выбора оптимальной цены, обеспечивающей максимум математического ожидания величины дохода, которое с учетом (5.21) вычисляется как

,

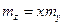(5.22)

где 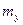, 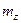– соответственно математические ожидания случайных величин 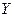и .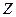

На розничную цену реализуемого товара наложим ограничение вида:

x o ≤ х ≤ х п.

(5.23)

Здесь x _o, х _п – соответственно значения рекомендуемой и предельной цен на рассматриваемый товар.

Если ТЦ имеет право проводить оптовые закупки товаров, то величина х _о определяется как оптовая цена рассматриваемого товара. Значение цены х _п назначается маркетологом ТЦ с учетом того, что при ней может быть обеспечен ненулевой спрос на товар. Кроме этого, значением х _п может быть существующая розничная цена на аналогичный товар у конкурентов.

Задача оптимизации

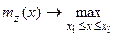
(5.24)

с учетом выражения (5.22) имеет очевидное решение вида:

, .

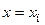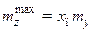(5.25)

Случайный характер дохода 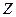вызывает разброс его реализаций, который отрицательно влияет на планирование деятельности вышестоящих организаций. Поэтому естественным требованием является выбор такого значения цены х, при котором дисперсия дохода в рассматриваемом промежутке времени была бы минимальной. Это приводит к задаче оптимизации вида:

,

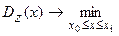(5.26)

где дисперсия случайной величины 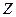с учетом (5.21) вычисляется как

.

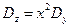(5.27)

В этом выражении 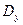– дисперсия случайной величины .

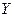Задача (5.26), (5.27) имеет очевидное решение:

, .

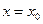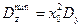(5.28)

Из выражений (5.25) и (5.24) видно, что задачи оптимизации (5.24) и (5.26) имеют несовпадающие решения, соответствующие граничным точкам интервала 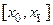. Решение двухкритериальной задачи будет рассмотрено позднее.