Определение. Непрерывная случайная величина  имеет нормальный закон распределения, если её плотность вероятности имеет вид:
имеет нормальный закон распределения, если её плотность вероятности имеет вид:
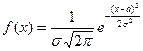 , где
, где 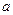 и
и  - параметры распределения.
- параметры распределения.
Параметры 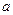 и
и  представляют собой соответственно математическое ожидание и среднеквадратическое отклонение этой случайной величины, т.е.
представляют собой соответственно математическое ожидание и среднеквадратическое отклонение этой случайной величины, т.е.
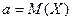 ,
, 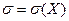 .
.
Отсюда 
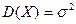 .
.
В частном случае при 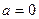
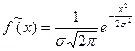 .
.
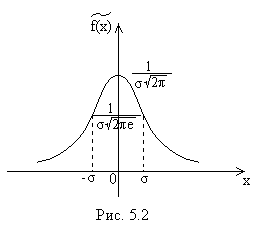
Рассмотрим график этой функции (рис. 5.2).
1) Кривая пересекает ось  в точке
в точке 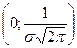 . Она является точкой максимума.
. Она является точкой максимума.
2) С осью 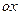 кривая не пересекается; ось
кривая не пересекается; ось 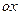 является асимптотой, так как
является асимптотой, так как
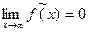 .
.
3) Кривая симметрична относительно оси  , так как функция
, так как функция 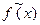 чётная.
чётная.
При 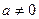 кривые
кривые  получаются путём сдвига на
получаются путём сдвига на 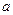 единиц по горизонтали кривой
единиц по горизонтали кривой 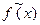 при тех же значениях параметра
при тех же значениях параметра  . Если
. Если  увеличивается, то кривая сжимается вдоль оси
увеличивается, то кривая сжимается вдоль оси  , с уменьшением
, с уменьшением  график функции
график функции 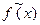 вытягивается. Таким образом, параметр
вытягивается. Таким образом, параметр 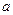 характеризует положение, а параметр
характеризует положение, а параметр  - форму нормальной кривой.
- форму нормальной кривой.
Для нормально распределённой случайной величины функция распределения равна
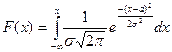 .
.
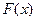 можно представить через функцию
можно представить через функцию 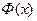 , значения которой затабулированы:
, значения которой затабулированы:
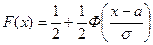 - функция распределения для нормального закона.
- функция распределения для нормального закона.
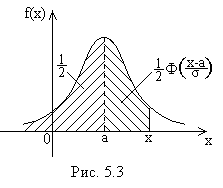
Геометрически функция распределения представляет собой площадь под нормальной кривой на интервале 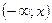 , которая состоит из двух частей: I часть соответствует площади под кривой на интервале
, которая состоит из двух частей: I часть соответствует площади под кривой на интервале 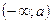 ,равной половине всей площади под нормальной кривой; II часть соответствует площади под кривой на интервале
,равной половине всей площади под нормальной кривой; II часть соответствует площади под кривой на интервале 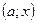 , равной
, равной 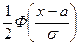 (рис. 5.3).
(рис. 5.3).
 2014-02-09
2014-02-09 461
461








