Ненулевое собственное значение l компактного самосопряженного оператора имеет конечную кратность, т. е. число линейно независимых собственных векторов, отвечающих собственному значению l, конечно (см. раздел 8.3).
Лемма 9.1. Пусть A : H ® H – компактный самосопряженный оператор в гильбертовом пространстве H. Для любого e > 0 число собственных значений, удовлетворяющих условию | l | ³ e, конечно.
Доказательство. Предположим противное. Пусть e 1, e 2, ¼, en, ¼ – бесконечная ортонормированыая последовательность, состоящая из собственных векторов с собственными значениями lk, где | lk | ³ e > 0. Тогда множество A ek = lk ek как образ ограниченного множества должно быть предкомпактным. Ho || A ek – A en || = || lk ek – ln en || =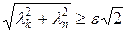 . Это означает, что из последовательности A ek нельзя выделить подпоследовательность Коши. Лемма доказана.
. Это означает, что из последовательности A ek нельзя выделить подпоследовательность Коши. Лемма доказана.
Следствие 9.1. Собственные значения l ¹ 0 самосопряженного компактного оператора с учетом кратности могут быть занумерованы в последовательность l 1, l 2, ¼, ln, ¼ так, что | lk | ³ | lk + 1| и lk ® 0 при k ® ¥.
Докажем теорему Гильберта о приведении к диагональному виду самосопряженного компактного оператора в сепарабельном гильбертовом пространстве.
Теорема 9.3 (Д. Гильберт). Пусть A – самосопряженный компактный оператор в сепарабельном гильбертовом пространстве H. Тогда в H существует полная ортонормированная система, состоящая из собственных векторов оператора A.
Доказательство. Для каждого ненулевого собственного значения l в пространстве Ker (A – l I) выберем ортогональный базис. Пусть L – подпространство в H, порожденное объединением всех выбранных базисов. Тогда L инвариантно относительно A и, значит, L ^ также инвариантно относительно A. Сужение оператора A на L ^ является самосопряженным компактным оператором. Покажем, что B = A | L = 0, т. е. что это нулевой оператор. Согласно теореме 9.2, существует спектральное значение m оператора B такое, что | m | = || B ||. Предположим, что || B || ¹ 0, т. е. m ¹ 0. Тогда по теореме 8.7 оператор B – m I фредгольмов и ind ( B – m I ) = 0. Если Ker ( B – m I ) = {0}, то Im ( B – m I ) = L ^ и, значит, B – m I имеет ограниченный обратный оператор. Следовательно, m, не является спектральным значением. Значит, Ker ( B – m I ) ¹ {0}, т. е. m есть собственное значение оператора A с собственным вектором v Î L ^. Но по построению все собственные векторы с ненулевыми собственными значениями принадлежат L. Получаем противоречие. Значит, || B || = 0 и все векторы из L ^ являются собственными векторами оператора A с собственным значением l = 0. Выберем в L ^ базис и, объединяя его с построенным ранее базисом в L, получаем базис в пространстве H, состоящий из собственных векторов оператора A. Теорема доказана.
Замечание 9.1. Сепарабельность пространства H использована только для построения счетного базиса в L ^. Поэтому для произвольных гильбертовых пространств аналогичная теорема формулируется следующим образом.
Теорема 9.4. Если A – самосопряженный компактный оператор в гильбертовом пространстве H, то существует инвариантное подпространство L Ì H такое, что в L есть счетный базис, состоящий из собственных векторов оператора A с ненулевыми собственными значениями, а на ортогональном дополнении L ^ оператор A нулевой.
Замечание 9.2. Если для оператора A в гильбертовом пространстве H существует полная ортонормированная система { ek } такая, что A ek = lk ek, причем lk вещественны и lk ® 0 при k ® ¥, то A – самосопряженный компактный оператор. Действительно, обозначая через An оператор, действующий по формуле
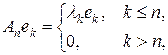
получаем, что An – оператор конечного ранга и, следовательно, компактен. Так как 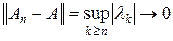 , то A компактен.
, то A компактен.
Замечание 9.3. Если оператор A действует в гильбертовом пространстве l 2, то он может быть задан бесконечной матрицей (ai j), его квадратичная форма имеет вид 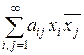 , т. е. является квадратичной формой бесконечного числа переменных xk. Если перейти к базису ek, состоящему из собственных векторов оператора A с собственными значениями lk, то квадратичная форма примет вид
, т. е. является квадратичной формой бесконечного числа переменных xk. Если перейти к базису ek, состоящему из собственных векторов оператора A с собственными значениями lk, то квадратичная форма примет вид 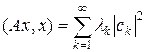 , где ck = (x, ek) – новые координаты вектора x. Таким образом, из теоремы Гильберта получаем, что квадратичная форма компактного самосопряженного оператора приводится к сумме квадратов.
, где ck = (x, ek) – новые координаты вектора x. Таким образом, из теоремы Гильберта получаем, что квадратичная форма компактного самосопряженного оператора приводится к сумме квадратов.
Простейшими операторами в гильбертовом пространстве являются проекторы P 2 = P, P * = P. Обозначим через Pk оператор проектирования на подпространство, порожденное собственным вектором ek, соответствующим собственному значению lk, Pk x = (x, ek) ek.
Проекторы P 1 и P 2 называются ортогональными друг к другу, если P 1 P 2 = P 2 P 1 = 0, т. е. если ортогональны подпространства, на которые они проектируют. Тогда теорему Гильберта можно сформулировать в следующем виде.
Теорема 9.5. Если A – самосопряженный компактный оператор, то существует последовательность попарно ортогональных проекторов Pk такая, что 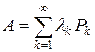 , причем lk ® 0 и ряд сходится по норме.
, причем lk ® 0 и ряд сходится по норме.
Пусть { ek } – базис в пространстве H, состоящий из собственных векторов оператора A с собственными значениями lk. Если 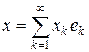 – разложение x Î H в ряд Фурье по этой сисгеме, то действие оператора A задается простой формулой
– разложение x Î H в ряд Фурье по этой сисгеме, то действие оператора A задается простой формулой
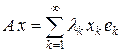 ,
,
которая позволяет определить функции от оператора
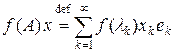 .
.
Оператор f (A) определен для функций, заданных и ограниченных на множестве собственных значений { lk }. В частности, если l – регулярное значение для оператора A, то определена резольвента оператора
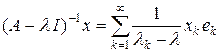 . (4)
. (4)
Формула (4) позволяет явно выписать решение уравнения A x – l x = y для регулярного значения l:
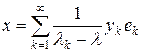 ,
,
где yk = (y, ek) – коэффициенты Фурье элемента y.
 2014-02-09
2014-02-09 1166
1166