Рис. 5.1
5.4.2 Основные правила преобразования структурных схем.
1) Последовательное соединение звеньев. При последовательном соединении выходная величина каждого предшествующего звена является входным воздействием последующего звена (рис. 5.2, а). Цепочку из последовательно соединенных звеньев можно заменить одним звеном (рис. 5.2, б) с передаточной функцией W(s), равной произведению передаточных функций отдельных звеньев:
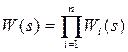
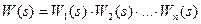 (5.12)
(5.12)



|

|
 у0 у1 у2 yn-1 уn у0 уn
у0 у1 у2 yn-1 уn у0 уn а) б)
Рис. 5.2
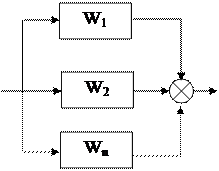
2) Параллельное соединение звеньев. При параллельном соединении на вход всех звеньев подается один и тот же сигнал, а выходные величины складываются. Цепь из параллельно соединенных звеньев (рис. 5.3, а) можно заменить одним звеном (рис. 5.3 б) с передаточной функцией W(s), равной сумме передаточных функций входящих в нее звеньев: 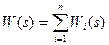 .
.
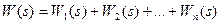 (5.13)
(5.13)
 y1
y1
 y2 y0 y
y2 y0 y
Y0 y
yn
а) б)
Рис. 5.3
3) Правила структурных преобразований при наличии обратных связей. Принято считать, что звено охвачено обратной связью (рис. 5.4, а), если его выходной сигнал через какое-либо другое звено подается на вход. При этом если сигнал у1 обратной связи вычитается из входного воздействия у0 , т.е. е1=у0-у1, то обратную связь называют отрицательной. Если сигнал у1 обратной связи складывается с входным воздействием у0, т.е. е1=у0+у1, обратную связь называют положительной.
Разомкнем обратную связь перед сравнивающим звеном (рис. 5.4, а). Тогда получим цепь из двух последовательно соединенных звеньев. Поэтому передаточная функция W разомкнутой цепи (рис. 5.4, а) равна произведению передаточной функции Wп прямой цепи и передаточной функции Wо.с. обратной связи: 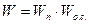 (рис. 5.4, б).
(рис. 5.4, б).
Передаточная функция Wз замкнутой цепи с отрицательной обратной связью, - равна передаточной функции прямой цепи, деленной на единицу плюс передаточная функция разомкнутой цепи:
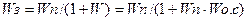 (5.14)
(5.14)
Передаточная функция замкнутой цепи с положительной обратной связью, - равна передаточной функции прямой цепи, деленной на единицу минус передаточная функция разомкнутой цепи.
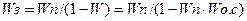 (5.15)
(5.15)
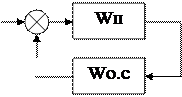 у0 е1
у0 е1
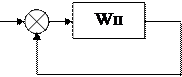
 у0 у1 у0 е1
у0 у1 у0 е1
_ _

 (+)»у1 (+)
(+)»у1 (+)
а) б) в)
Рис. 5.4
Если передаточная функция Wо.с.=1, то обратная связь называется единичной и структурная схема изображается так, как показано на рис. 5.4, в. Передаточная функция Wз при этом принимает вид 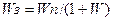 при отрицательной обратной связи и
при отрицательной обратной связи и 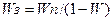 при положительной обратной связи.
при положительной обратной связи.
4) Перенос сумматора (рис. 5.5). Легко показать, что при переносе сумматора по ходу сигнала необходимо добавить звено с передаточной функцией, равной передаточной функции звена, через которое переносится сумматор (рис.5.5, а). Если сумматор переносится против хода сигнала, то необходимо добавить звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится сумматор (рис. 5.5,б).
При переносе сумматора возникают неэквивалентные участки линии связи. Эти участки на рис. 5.5 заштрихованы.
 z
z
 z
z
у0 у1 e1 y2 у0 у1 y2
а)
 |
z
 z
z
у0 у1 e1 y2 у0 e1 y2
 |
б)
Рис. 5.5
5) Перенос узла (рис. 5.6, а). При переносе узла также необходимо добавить звено. Если узел переносится по ходу сигнала, то добавляется звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится узел (рис.5.6,б). Если узел переносится против хода сигнала, то добавляется звено передаточной функции звена, через которое переносится узел (рис.5.6, в).
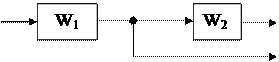 у0 у1 у2
у0 у1 у2
а)
у1
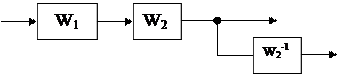 у0 у1 у2
у0 у1 у2
б)
у1
|
|
 в)
в)

у1
Рис. 5.6
6) Вычисление передаточной функции одноконтурной системы.
Замкнутую систему (структурную схему) называют одноконтурной, если при ее размыкании в какой-либо точке получается цепочка из последовательно соединенных звеньев или цепь, не содержащая параллельных и обратных связей.
На рис.5.7, а приведена одноконтурная система. Найдем передаточную функцию по входу g и выходу y.
Справедливо следующее правило: передаточная функция одноконтурной системы с отрицательной (положительной) обратной связью равна передаточной функции прямой цепи, деленной на единицу плюс (минус) передаточная функция разомкнутой цепи:
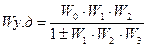 (5.16)
(5.16)
Сформулированное правило справедливо для любой одноконтурной системы.
Прямая цепь

g y
а)
_
(+)
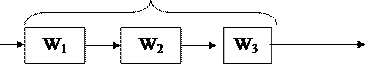 Разомкнутая цепь
Разомкнутая цепь
б)
Рис. 5.7
7) Вычисление передаточной функции многоконтурной системы.
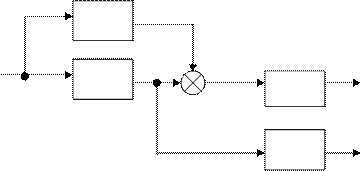
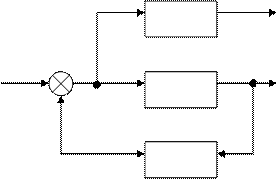
Замкнутую систему (структурную схему) называют многоконтурной, если при ее размыкании получается цепь, содержащая параллельные или обратные связи, или, иначе, если она помимо главной обратной связи содержит местные обратные или параллельные связи. Говорят, что многоконтурная система имеет перекрещивающие связи, если контур обратной или параллельной связи охватывает участок цепи, содержащий только начало или конец другой цепи обратной или параллельной связи (рис.5.8, а, б).
Для вычисления передаточной функции многоконтурной системы необходимо прежде всего перестановкой и переносом узлов и сумматоров освободится от перекрещивающихся связей. Затем, использую первые три правила преобразования схем, преобразовать ее в одноконтурную систему, передаточную функцию которой легко вычислить согласно сформулированному выше правилу. Следует помнить, что при преобразовании структурной схемы нельзя переносить сумматор через точку съема выходного сигнала, так как при этом точка съема оказывается на неэквивалентном участке.
 |
а)
 |
б)
Рис.5.8
Пример. Определим передаточные функции системы, приведенной на рис.5.9,а, по ”входам” g и f и “выходам” y и e. Эта система является многоконтурной с перекрещивающимися обратными связями. Перенеся и переставив сумматоры, ее можно привести к многоконтурной системе без перекрещивающихся связей (рис.5.9,б). После замены параллельно соединенных звеньев и звена, охваченного обратной связью, эквивалентными звеньями с передаточной функцией 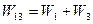 ;
; 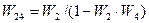 получим одноконтурную схему (рис.5.9,в).
получим одноконтурную схему (рис.5.9,в).
При вычислении передаточной функции по входному воздействию g полагаем f=0. Согласно правилу вычисления передаточной функции одноконтурных систем:
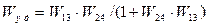 ;
;
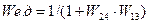
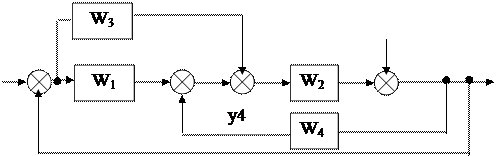
При вычислении передаточной функции по входному воздействию f g полагаем g=0. При этом сравнивающее звено становится инвертирующим звеном с передаточной функцией, равной (-1). Инвертирующее звено в замкнутый контур можно не вводить, если суммирующее звено преобразовать в сравнивающее. Поэтому структурную схему можно представить так, как это показано на рис.5.9, г.
Из этой схемы очевидно:
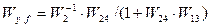
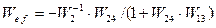
 y3
y3
f
y1 e1 y2
g y
а)
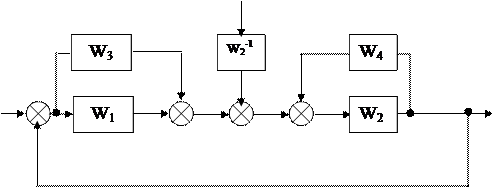 |
f
g e y1
y
- б)
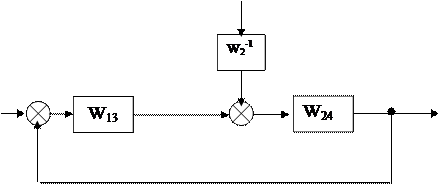 f
f
g e
y в)
-
y
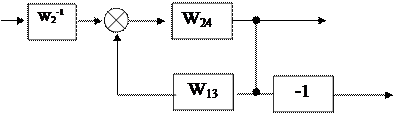 f
f
г)
e
Рис. 5.9
6.1. Временные характеристики.
Важной характеристикой систем автоматического управления являются переходные и импульсные функции и их графики - временные характеристики. Их используют при описании линейных систем, как стационарных, так и нестационарных.
Переходной функцией системы (звена) называют функцию, описывающую изменение выходной величины системы (звена) когда на ее вход подается единичное ступенчатое воздействие при нулевых начальных условиях. Переходную функцию обозначают h(t). Иначе: переходная функция h(t)3 есть функция, описывающая реакцию системы (звена) на единичное ступенчатое воздействие при нулевых начальных условиях.
График переходной функции – кривая зависимости функции h(t) от времени t - называют переходной или разгонной характеристикой.
Импульсной переходной или весовой функцией (функцией веса) системы называют функцию, описывающую реакцию системы на единичное импульсное воздействие при нулевых начальных условиях; обозначают эту функцию w(t).
График импульсной переходной функции называют импульсной переходной характеристикой.
Переходную и импульсную переходную характеристики называют временными характеристиками.
 X(t)=1(t) Y(t)=h(t)
X(t)=1(t) Y(t)=h(t)
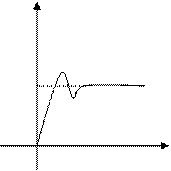
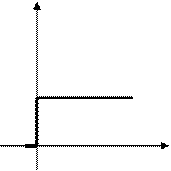 Х h Y
Х h Y
a)
0 t 0 t
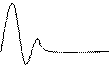
 X x(t)=s(t) y(t)=w(t)
X x(t)=s(t) y(t)=w(t) 
Y
 |


 б)
б)

 t t
t t
Рис.6.1 К определению переходной функции а) и функции веса звена б).
Переходная функция может быть определена экспериментально или вычислена аналитически.
Если работа звена описывается дифференциальным уравнением, то для аналитического определения переходной функции необходимо найти решение дифференциального уравнения при нулевых начальных условиях.
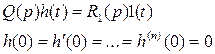
Воспользовавшись преобразованием Лапласа, получим изображение переходной функции
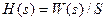 , (6.1)
, (6.1)
т.к. 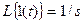

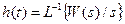 (6.2)
(6.2)
Таким образом переходная функция представляет собой обратное преобразование Лапласа от передаточной функции звена, деленной на s.
Если система описывается дифференциальным уравнением выше третьего порядка n>3, для получения функции h(t) целесообразно использовать компьютер.
Результаты вычисления переходной функции обычно представляют в виде графика, построенного в координатах (t, h), (см.6.1.а).
Функция веса (импульсная переходная функция) может быть найдена аналитически и экспериментально.
Для экспериментального определения функции веса осциллографируют процесс изменения выходной величины звена (системы) при входном воздействии в виде реального импульса с единичной площадью. Возникшая при этом методическая поверхность будет тем меньше, чем меньше длительность входного импульса по сравнению с временем затухания переходных процессов в исследуемом звене.
Для аналитического определения функции веса звена, необходимо решить дифференциальное уравнение при нулевых начальных условиях.
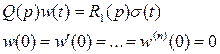
Преобразовав это выражение по Лапласу получим:
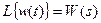 , (6.3)
, (6.3)
т.к. 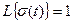
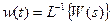 (6.4)
(6.4)
Таким образом, функция W(s) веса звена представляет собой обратное преобразование Лапласа от передаточной функции звена.
Если функция W(s) является правильной рациональной дробью, то практические расчеты при помощи выражения (6.4) могут быть выполнены по теореме разложения (7-ое свойство преобразования Лапласа).
Результаты вычисления функции веса могут быть представлены в виде графика, построенного в координатах (t, w) (см. рис. 6.1,б).
К преимуществам временных характеристик перед передаточными функциями и дифференциальными уравнениями относится возможность их экспериментального определения и наглядность.
6.2. Частотные характеристики.
Для определения характера переходного процесса в системах автоматического управления удобно пользоваться временными характеристиками. Однако в реальных системах очень часто входной сигнал изменяется по гармоническому закону заданной амплитуды и частоты.
При исследовании САР ставится задача нахождения параметров колебаний на выходе системы по известным параметрам колебаний на входе.
Частотный метод позволяет получить реакцию звена (системы) на любой периодический сигнал.
Для линейных систем справедлив принцип суперпозиции, который можно сформулировать следующим образом: реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет ограничиться изучением систем только с одним входом.
Если задана передаточная функция W(s)=W(p), то путем подстановки: 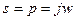 получаем
получаем 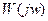 -данную функцию называют частотная передаточная функция.
-данную функцию называют частотная передаточная функция.
Частотная передаточная функция является комплексной функцией от действительной переменной w, которая называется частотной.
Функцию 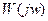 можно представить в виде:
можно представить в виде:
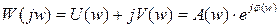 (6.5)
(6.5)
где 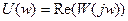 ;
; 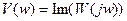 (6.6)
(6.6)
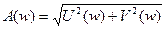 ;
; 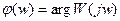 (6.7)
(6.7)
Если 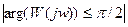 , то
, то
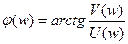 (6.8)
(6.8)
Модуль 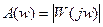 называют амплитудной частотной функцией, ее график - амплитудной частотной характеристикой (А.Ч.Х).
называют амплитудной частотной функцией, ее график - амплитудной частотной характеристикой (А.Ч.Х).
Аргумент 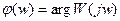 называют фазовой частотной функцией, ее график - фазовой частотной характеристикой (Ф.Ч.Х.)
называют фазовой частотной функцией, ее график - фазовой частотной характеристикой (Ф.Ч.Х.)
Функции 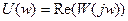 и
и 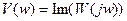 называются соответственно вещественной и мнимой частотной функцией. Их графики вещественной и мнимой частотными характеристиками системы (звена).
называются соответственно вещественной и мнимой частотной функцией. Их графики вещественной и мнимой частотными характеристиками системы (звена).
На комплексной плоскости (рис.6.2.) частотная передаточная функция 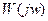 определяет вектор
определяет вектор 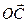 , длина которого равна
, длина которого равна 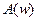 , а аргумент (угол, образованный этим вектором с действительной положительной полуосью)-
, а аргумент (угол, образованный этим вектором с действительной положительной полуосью)- 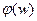 . Кривую (годограф), которую описывает конец вектора
. Кривую (годограф), которую описывает конец вектора 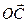 при изменении частоты от 0 до ¥, называют амплитудно-фазовой частотной характеристикой (А.Ф.Ч.Х.)
при изменении частоты от 0 до ¥, называют амплитудно-фазовой частотной характеристикой (А.Ф.Ч.Х.)
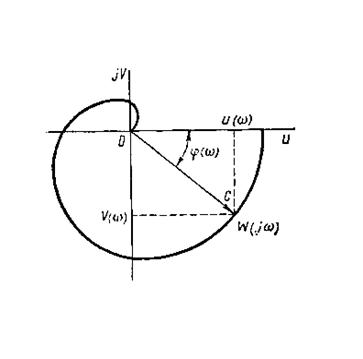
Рис.6.2
Таким образом, для определенной частоты имеем вектор на комплексной плоскости, который характеризуется модулем 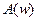 и аргументом
и аргументом 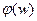 . Модуль
. Модуль 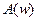 представляет собой численное отношение амплитуды выходного сигнала по отношению к входному. При этом отрицательный фазовый сдвиг представляется вращением вектора на комплексной плоскости по часовой стрелке относительно вещественной положительной оси, а положительный фазовый сдвиг представляется вращением против часовой стрелки (рис.6.2).
представляет собой численное отношение амплитуды выходного сигнала по отношению к входному. При этом отрицательный фазовый сдвиг представляется вращением вектора на комплексной плоскости по часовой стрелке относительно вещественной положительной оси, а положительный фазовый сдвиг представляется вращением против часовой стрелки (рис.6.2).
Из приведенной физической интерпретации частотных характеристик ясно, как строить их экспериментальным путем. Для экспериментального построения частотных характеристик имеется специальная аппаратура, в состав которой входят генератор гармонических колебаний с регулируемой частотой и устройства для измерения амплитуды и фазы колебаний.
Частотные характеристики используют для описания как устойчивых, так и неустойчивых систем. Но в последнем случае они не имеют такого ясного физического смысла.
6.3. Логарифмические частотные характеристики.
Частотные методы исследования линейных систем автоматического управления существенно упростились после того как для построения графиков частотных характеристик были введены логарифмические шкалы.
Частотные характеристики, построенные в логарифмических шкалах, называются логарифмическими частотными характеристиками.
Чаще всего строятся характеристики 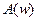
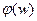 и
и 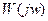 , называемые соответственно логарифмической амплитуно - частотной характеристикой (ЛАЧХ), логарифмической фазо - частотной характеристикой (ЛФЧХ), и логарифмической амплитудно-фазовой частотной характеристикой (ЛАФЧХ).
, называемые соответственно логарифмической амплитуно - частотной характеристикой (ЛАЧХ), логарифмической фазо - частотной характеристикой (ЛФЧХ), и логарифмической амплитудно-фазовой частотной характеристикой (ЛАФЧХ).
При построении логарифмических характеристик на шкале частот вместо w откладывается lg w. Единицами измерения логарифмических координат является декада (дек) и децибел (дб). Логарифм - величина безразмерная и указание единиц измерения вводится условно, для удобства. Декадой называется интервал частот, соответствующей изменению частоты в 10 раз. На логарифмической шкале декада изображается отрезком единичной длины, так как Lg 10w - Lg w=1.
Поэтому относительно величины lg 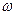 логарифмическая шкала является равномерной, а относительно частоты - неравномерной (рис.6.3).
логарифмическая шкала является равномерной, а относительно частоты - неравномерной (рис.6.3).
 -3 -2 -1 0 1 2 3 4 5
-3 -2 -1 0 1 2 3 4 5 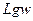 , (дек)
, (дек)
 0.001 0.01 0.1 1 10 100 1000 104 105 w, (сек-1)
0.001 0.01 0.1 1 10 100 1000 104 105 w, (сек-1)
Рис. 6.3. Логарифмическая шкала
Децибел используется при введении логарифмической шкалы по оси ординат амплитудно - частотной характеристики (АЧХ), которая, показывает, во сколько раз амплитуда выходного сигнала больше или меньше амплитуды входного сигнала. Усилением в децибелах называется величина 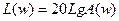 . Усилению соответствуют положительные децибелы, а ослаблению - отрицательные. В натуральном масштабе 1дб соответствует усилению в 1,12 раза, т.е. 20Lg1.12
. Усилению соответствуют положительные децибелы, а ослаблению - отрицательные. В натуральном масштабе 1дб соответствует усилению в 1,12 раза, т.е. 20Lg1.12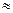 1, кроме того А=10L/20. Таким образом, получается, что 1дб = 1/20 дек. Смысл введения по шкале частот декады, а по оси усиление децибела, заключается в том, чтобы при изменении w от 0 до ¥ усиление (ослабление) по амплитуде изменялось в заметных пределах (усилению в 1 млн. раз соответствует всего лишь 6 декад).
1, кроме того А=10L/20. Таким образом, получается, что 1дб = 1/20 дек. Смысл введения по шкале частот декады, а по оси усиление децибела, заключается в том, чтобы при изменении w от 0 до ¥ усиление (ослабление) по амплитуде изменялось в заметных пределах (усилению в 1 млн. раз соответствует всего лишь 6 декад).
Ниже приводится соотношение между величинами А и L (таб.6.1).
Таб. 6.1.
| A | 0.1 | 0.2 | 1.12 | 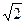 | 106 | ||||||
| L | -20 | -14 |
Чтобы получить ЛАЧХ, необходимо взять функцию 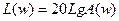 и построить ее график, используя логарифмическую шкалу частот.
и построить ее график, используя логарифмическую шкалу частот.
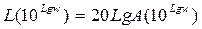 .
.
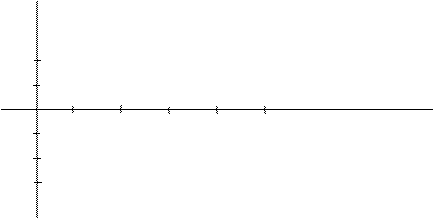
При построении ЛФЧХ логарифмическая шкала применяется только по оси частот, а по оси ординат используется натуральный масштаб. Для практических расчетов оказывается удобным при изображении ЛАЧХ и ЛФЧХ использовать одну и ту же ось частот, совместив точку –1800 оси ординат ЛФЧХ с точкой 0 дб ординат ЛАЧХ (рис.6.4).
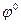
 L, дб
L, дб
-360
-270
-180 0 1 2 3 4 5 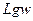 , (дек)
, (дек)
10 100 103 104 105 w, (сек-1)
-90
+90
Рис. 6.4 Оси системы координат ЛАЧХ и ЛФЧХ.
В некоторых случаях построение совмещенной системы координат выполняют таким образом, что совмещается точка 00 оси ординат ЛФЧХ с точкой 0 дб оси ординат ЛАЧХ (рис.6.5).
Логарифмическая амплитудно-частотная и логарифмическая фазо-частотная характеристики представлены на рис.6.5. На практике обычно ограничиваются построением так называемой асимптотической ЛАЧХ (ломаная линия на том же рис.6.5). Только в особых случаях, когда небольшая погрешность может повлиять на выводы, рассматривают точную ЛАЧХ. Впрочем, точную ЛАЧХ можно легко построить по асимптотической ЛАЧХ если воспользоваться следующей зависимостью (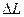 - разность между асимптотической и точной ЛАЧХ) таблица 6.2.:
- разность между асимптотической и точной ЛАЧХ) таблица 6.2.:
Таблица 6.2.
| Т w | 0.1 | 0.25 | 0.4 | 0.5 | 1.0 | 2.0 | 2.5 | 4.0 | |
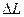 | 0.04 | 0.25 | 0.62 | 0.96 | 3.0 | 0.96 | 0.62 | 0.25 | 0.04 |
Частоту ws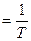 (на рис. 6.5.- w1), при которой пресекаются асимптоты, называют сопрягающей. Точная и асимптотическая ЛАЧХ наиболее сильно отличаются при сопрягающей частоте; отклонение при этой частоте примерно равно 3 дб.
(на рис. 6.5.- w1), при которой пресекаются асимптоты, называют сопрягающей. Точная и асимптотическая ЛАЧХ наиболее сильно отличаются при сопрягающей частоте; отклонение при этой частоте примерно равно 3 дб.
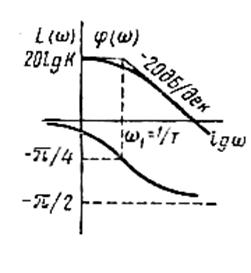
Рис.6.5
Пример. Построение логарифмических частотных характеристик системы автоматического управления.
Пусть система состоит из трех последовательно соединенных звеньев и описывается передаточной функцией
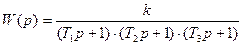 ,
,
где Т1=1с, Т2=0,1с, Т3=0,03с, к=180
Заменив в передаточной функции p на 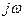 и прологарифмировав полученные выражения, найдем:
и прологарифмировав полученные выражения, найдем:
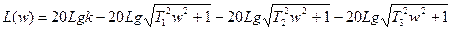 ;
;
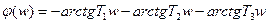
Сопрягающие частоты: w1=1/T1=1c-1; w2=1/T2=10c-1; w3=1/T3=33,3c-1.
График 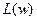 (рис.6.6) строится следующим образом. За начало отсчета по оси w примем w= 0,1.Отложив по оси ординат 20Lg 180=45дБ, проводим прямую АВ, параллельную оси абсциссс, до сопрягающей частоты w1=1.Так как каждая из составляющих ЛАЧХ (второй, третий и четвертый члены правой части выражения для (
(рис.6.6) строится следующим образом. За начало отсчета по оси w примем w= 0,1.Отложив по оси ординат 20Lg 180=45дБ, проводим прямую АВ, параллельную оси абсциссс, до сопрягающей частоты w1=1.Так как каждая из составляющих ЛАЧХ (второй, третий и четвертый члены правой части выражения для (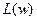 ) имеет отрицательный наклон -20дб/дек, проводим прямую, проходящую через точку В с наклоном 20дб/дек, до сопрягающей частоты w2=10 (точка С). Через точку С проводим прямую с отрицательным наклоном -40дб/дек до сопрягающей частоты w3=33,3 (точка D). Последняя асимптота DE, уходящая в бесконечность, проводится через точку D с отрицательным наклоном - 60дб/дек. Логарифмическая фазовая характеристика
) имеет отрицательный наклон -20дб/дек, проводим прямую, проходящую через точку В с наклоном 20дб/дек, до сопрягающей частоты w2=10 (точка С). Через точку С проводим прямую с отрицательным наклоном -40дб/дек до сопрягающей частоты w3=33,3 (точка D). Последняя асимптота DE, уходящая в бесконечность, проводится через точку D с отрицательным наклоном - 60дб/дек. Логарифмическая фазовая характеристика строится по точкам (рис.6.6).
строится по точкам (рис.6.6).
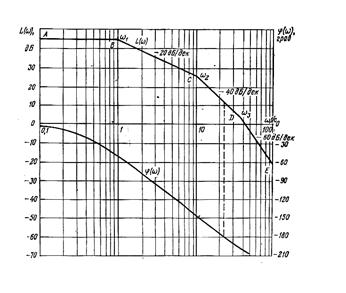
Рис.6.6. Логарифмические амплитудная и фазовая частотные характеристики ЛАЧХ - L(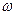 ), ЛФЧХ -
), ЛФЧХ - 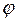 (
( )
)
 2014-02-09
2014-02-09 2718
2718
