Разработка оптимальной программы снижения риска

Вопрос №3.

Снижение интегральной оценки риска достигается за счет проведения мероприятий, снижающих локальные риски по различным направлениям. Так для нашего примера имеются направления снижения риска: направление 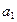связано с мероприятиями, снижающими экономический риск, направление 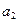- экологический риск, направление 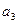- риск людских потерь и направление 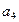- риск ухудшения условий жизни. Примем для определенности, что исходное состояние объекта характеризуется высокими локальными рисками (оценки 3) по всем направлениям. Соответственно, интегральная оценка также равна 3 (высокий или существенный риск). Снижение локального риска по каждому направлению требует затрат на проведение соответствующих мероприятий. Обозначим 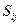- затраты на снижение локального риска по направлению 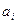до оценки j,

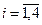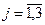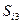, (соответствует затратам на поддержание локального риска на том же уровне). Поставим задачу разработать вариант программы снижения интегрального риска до оценки 2 (средний или ощутимый риск) с минимальными затратами. Каждый вариант программы будем описывать вектором локальных рисков. Так вариант (2, 1, 2, 3) означает, что реализация программы обеспечивает снижение экономического риска до среднего уровня, экологического - до низкого уровня, риска людских потерь - до среднего уровня, а риск ухудшения условий жизни остается высоким. Интегральный риск при этом равен 2, то есть данный вариант программы является допустимым. Затраты на реализацию данного варианта составляют: .

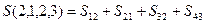Для разработки программы минимальной по стоимости можно рассмотреть все допустимые варианты и выбрать из них вариант с минимальными затратами. Однако, при большом числе локальных рисков и большом числе возможных оценок локальных рисков число допустимых вариантов становится большим и простой перебор не эффективен.

Определение. Вариант программы называется напряженным, если увеличение локального риска хотя бы по одному направлению приводит к увеличению интегрального риска.

Важность понятия напряженного варианта связана с тем, что как легко показать, оптимальный вариант программы является напряженным вариантом. Действительно, пусть имеется допустимый, не напряженный вариант. Тогда существует направление, по которому можно увеличить локальный риск без изменения оценки интегрального риска. Очевидно, что новый вариант является допустимым и требует меньших затрат. Опишем алгоритм построения всех напряженных вариантов. Заметим, что напряженный вариант по существу является Парето-оптимальным вариантом. Определение Парето-оптимальных вариантов при дискретных шкалах оценок - задача известная и для двух критериев (обобщенных оценок, свертка которых определяется одной матрицей) алгоритм также известен. Дадим его краткое описание.

Рассматриваем последний столбец матрицы и определяем максимальную строку с требуемой оценкой. Напоминаем, что в нашем случае нумерация столбцов идет справа налево, а строк - сверху вниз. Для этой строки определяем максимальный столбец с требуемой оценкой. Эта оценка будет определять напряженный вариант. Далее, начиная со столбца с меньшим номером (на единицу), повторяем процедуру, и т.д. Будем для краткости обозначать этот базовый алгоритм символом Н. Для описания всех напряженных вариантов применяем алгоритм Н к матрице интегральной оценки (корневая вершина дерева критериев). Заметим, что каждому напряженному варианту матрицы интегральной оценки соответствуют две обобщенные оценки следующего уровня дерева критериев. Для каждой из них находим все напряженные варианты в соответствующих матрицах обобщенных оценок (применяя алгоритм Н). Продолжаем таким образом строить сеть напряженных вариантов. Эта сеть для нашего примера приведена на рис. 8.

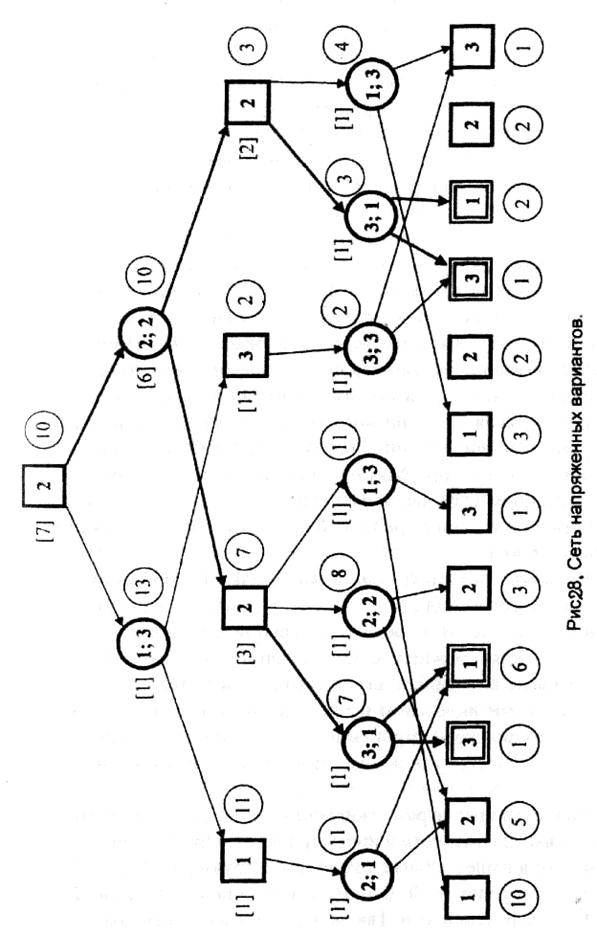
В ней чередуются вершины двух типов. Вершины одного типа обозначены квадратами, в которых указаны значения обобщенных оценок, для которых нужно определить напряженные варианты в соответствующих матрицах (вход сети всегда квадрат, в котором указано значение комплексной оценки, а выходы - квадраты, в которых указаны значения оценок по направлениям). Вершины-квадраты соединены дугами с вершинами-кружками, в которых указаны все напряженные варианты для данной обобщенной оценки. Любому напряженному варианту соответствует прадерево (подграф сети) с корнем в начальной вершине. В каждую вершину-кружок этого прадерева заходит только одна дуга от вершины-квадрата более высокого уровня, а из каждой вершины-кружка выходят две дуги к вершинам-квадратам более низкого уровня (на рис. 8 один из вариантов выделен жирным дугами). Построив сеть напряженных вариантов, нетрудно определить их число.

Для этого присваиваем выходным вершинам сети (квадратам) индекс 1. Индексы вершин-кружков получаются произведением индексов смежных им вершин-квадратов нижнего уровня, а индексы вершин-квадратов получаются сложением индексов смежных им вершин-кружков нижнего уровня. Двигаясь таким образом снизу вверх, определяем индекс входной вершины сети. Значение этого индекса определяет число напряженных вариантов. Для сети рис. 8 число напряженных вариантов равно семи (индексы указаны в квадратных скобках у соответствующих вершин).

Пусть построена сеть напряженных вариантов. Для определения варианта минимальной стоимости присваиваем выходам сети индексы, равные затратам на реализацию соответствующих мероприятий. Двигаясь снизу вверх, определяем индексы остальных вершин. При этом индекс вершин-кружков равен сумме индексов соответствующих вершин-квадратов более низкого уровня, а индекс вершин квадратов равен минимальному из индексов смежных с ним вершин-кружков более низкого уровня. Индекс вершины-входа будет равен величине минимальных затрат. Обоснование алгоритма следует из очевидного факта, что индекс любой вершины-квадрата при описанном способе вычисления индексов равен минимальным затратам на получение требуемой величины соответствующей обобщенной оценки.

Вариант, соответствующий минимальной стоимости определяется алгоритмом «обратного хода». Начиная с вершины верхнего уровня (входа сети), определяем вершину-кружок с минимальным индексом. Для смежных с ней вершин-квадратов более низкого уровня также определяем вершины-кружки более низкого уровня с минимальными индексами и т.д. Если оптимальных вариантов несколько, то можно построить подсеть оптимальных вариантов.

Для матрицы затрат, изображенной на рис. 8, оптимальный вариант выделен на сети жирными дугами. Оптимальный набор мероприятий в нашем случае получился следующим: 3, 1, 3, 1, а функционал цели равным 10. Выбранные мероприятия на рис 8 выделены двойными линиями. Таким образом, задача решена.