Т е м а. Классификация уравнений с частными производными второго порядка. Преобразование уравнений. Уравнения характеристик и общие интегралы. Канонический вид гиперболических, параболических и эллиптических уравнений
Л е к ц и и 3 - 4.
Общий вид уравнений с частными производными второго порядка можно записать в виде соотношений между независимыми переменными, искомой функцией и ее частными производными первого и второго порядков:
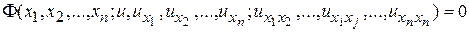 .
.
Очень часто эти уравнения являются линейными относительно старших производных – производных второго порядка, то есть, имеют вид:
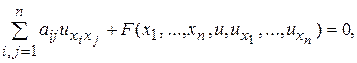
где коэффициенты при старших производных 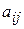 являются функциями только независимых переменных
являются функциями только независимых переменных 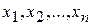 . Если коэффициенты
. Если коэффициенты 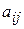 зависят не только от
зависят не только от 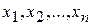 , а являются, подобно F, функциями
, а являются, подобно F, функциями 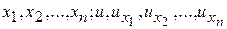 , то такое уравнение называется квазилинейным. Если функция
, то такое уравнение называется квазилинейным. Если функция 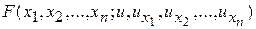 линейна относительно аргументов
линейна относительно аргументов 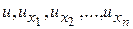 , то уравнение называется линейным. Линейные уравнения имеют вид:
, то уравнение называется линейным. Линейные уравнения имеют вид:
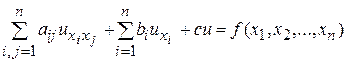 , (1)
, (1)
где коэффициенты 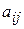 ,
, 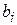 c являются функциями только независимых переменных
c являются функциями только независимых переменных 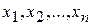 . Если
. Если 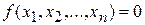 , то уравнение (1) называется линейным однородным, в противном случае - неоднородным. Если коэффициенты
, то уравнение (1) называется линейным однородным, в противном случае - неоднородным. Если коэффициенты 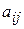 ,
, 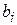 c постоянны, уравнение (1) называется линейным уравнением с постоянными коэффициентами.
c постоянны, уравнение (1) называется линейным уравнением с постоянными коэффициентами.
Все многообразие уравнений линейных относительно старших производных может быть разделено на три класса (типа). В каждом классе есть простейшие уравнения, которые называют каноническими. Решения уравнений одного и того же типа (класса) имеют много общих свойств.
Принадлежность уравнения к тому или иному классу (типу) – классификация уравнений – определяется коэффициентами при старших производных. Мы проведем классификацию прежде всего для уравнений, в которых искомая функция u зависит лишь от двух переменных: u = u (x, y). В этом случае уравнения, линейные относительно старших производных, можно записать в виде:
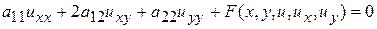 , (2)
, (2)
где 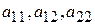 являются функциями x и y. А линейные уравнения – в виде:
являются функциями x и y. А линейные уравнения – в виде:
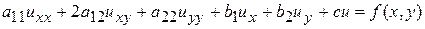 , (3)
, (3)
где 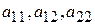 ,
, 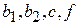 - функции только от x и y. Любое такое уравнение (2) и (3) с помощью замены независимых переменных может быть приведено к более простому – каноническому виду.
- функции только от x и y. Любое такое уравнение (2) и (3) с помощью замены независимых переменных может быть приведено к более простому – каноническому виду.
При помощи замены переменных
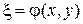 ,
, 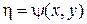 , (4)
, (4)
где 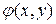 ,
, 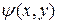 - дифференцируемые функции, преобразуем исходные уравнения к наиболее простому виду. Вычислим частные производные
- дифференцируемые функции, преобразуем исходные уравнения к наиболее простому виду. Вычислим частные производные
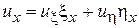 ,
, 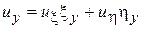 ,
,
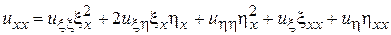 , (5)
, (5)
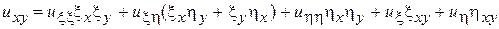 ,
,
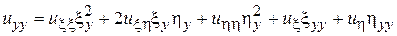 .
.
Подставляя значения производных из (5) в уравнение (2), будем иметь
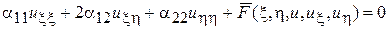 , (5а)
, (5а)
где
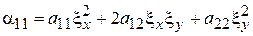 ,
,
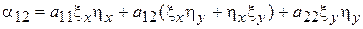 , (6)
, (6)
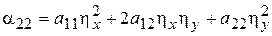 .
.
Заметим, что если уравнение линейно, то
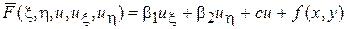 ,
,
где
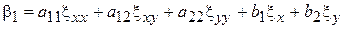 ,
,
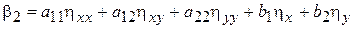 .
.
Непосредственной проверкой устанавливаем справедливость тождества
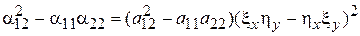 . (7)
. (7)
Обозначим через 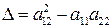 - дискриминант исходного уравнения в частных производных второго порядка. Из этого тождества следует, что знаки дискриминанта исходного и преобразованного уравнения одинаковые.
- дискриминант исходного уравнения в частных производных второго порядка. Из этого тождества следует, что знаки дискриминанта исходного и преобразованного уравнения одинаковые.
Теперь мы можем принять следующую классификацию уравнений вида (2).
Если в некоторой области D дискриминант 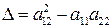 положителен,
положителен, 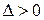 , то уравнение (2) называется гиперболическим в D (гиперболического типа в D).
, то уравнение (2) называется гиперболическим в D (гиперболического типа в D).
Если 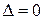 во всех точках области D, то уравнение (2) называется параболическим в D (параболического типа в D).
во всех точках области D, то уравнение (2) называется параболическим в D (параболического типа в D).
Если 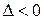 в области D, то уравнение (2) называется эллиптическим в D (эллиптического типа в D).
в области D, то уравнение (2) называется эллиптическим в D (эллиптического типа в D).
Из тождества (7) следует, что при замене независимых переменных по формулам (4) тип уравнения (2) не изменяется.
Приведем уравнение (2) к каноническому виду. Для каждого типа уравнения существует своя каноническая форма.
Рассмотрим теперь задачу преобразования исходного уравнения в частных производных к более простому виду, например, преобразуем так, чтобы в преобразованном уравнении коэффициенты 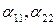 в области
в области 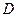 оказались равными нулю, то есть
оказались равными нулю, то есть
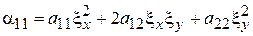 =0
=0
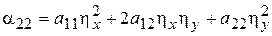 =0.
=0.
Представим эти уравнения в виде:
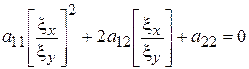 ,
,
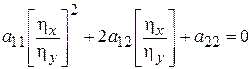 .
.
Разрешив их относительно 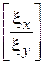 и
и 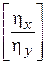 , получим:
, получим:
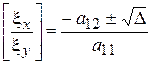 и
и 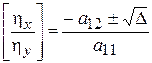 , (8)
, (8)
где 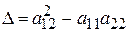 . Квадратные уравнения имеют одинаковые коэффициенты, следовательно, будут иметь одинаковые корни. Обозначим эти корни как
. Квадратные уравнения имеют одинаковые коэффициенты, следовательно, будут иметь одинаковые корни. Обозначим эти корни как
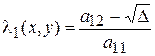 и
и 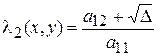 .
.
В этих выражениях предполагается, что 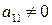 . Если это условие не выполнено, то уравнения будут линейными, и будут иметь простые решения. Решения квадратных уравнений можно записать в виде
. Если это условие не выполнено, то уравнения будут линейными, и будут иметь простые решения. Решения квадратных уравнений можно записать в виде
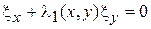 ,
, 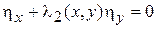 . (9)
. (9)
Докажем, что система уравнений в частных производных (10) эквивалентна системе обыкновенных дифференциальных уравнений:
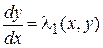 и
и 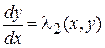 . (10)
. (10)
В самом деле, пусть функции 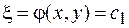 и
и 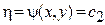 есть общие интегралы уравнений (10), то есть, постоянны вдоль решения этой системы.
есть общие интегралы уравнений (10), то есть, постоянны вдоль решения этой системы.
Тогда полное приращение этих функций вдоль решения будет равен нулю:
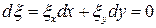 ,
, 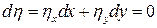 .
.
Откуда получим
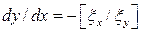 ,
, 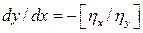 .
.
В силу равенств (10) получим
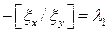 ,
, 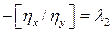 .
.
Преобразуя эти равенства, получим 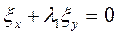 ,
, 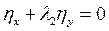 . То есть, все решения системы (10) являются также решениями системы (9). Можно доказать, что верно и обратное утверждение. Следовательно, системы (9) и (10) эквивалентны.
. То есть, все решения системы (10) являются также решениями системы (9). Можно доказать, что верно и обратное утверждение. Следовательно, системы (9) и (10) эквивалентны.
Общие интегралы уравнений (10) 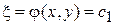 и
и 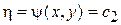 образуют два семейства кривых, называемых характеристиками уравнения (3). Уравнения (10) называются дифференциальными уравнениями характеристик.
образуют два семейства кривых, называемых характеристиками уравнения (3). Уравнения (10) называются дифференциальными уравнениями характеристик.
 2014-02-09
2014-02-09 2858
2858
