2014-02-12
1533
Лекция 2. Линейные дифференциальные уравнения 1-го порядка. Уравнения Бернулли. Уравнения в полных дифференциалах.
Линейные дифференциальные уравнения занимают особое место в инженерной практике. Решение многих задач геометрии также приводит к этому виду уравнений. Уравнения Бернулли интересны тем, что достаточно просто сводятся к линейным. Но не только этим: широк класс практических задач, приводящих к уравнениям Бернулли. Уравнения в полных дифференциалах важны тем, что затрагивают раздел математического анализа для функций нескольких переменных. Но и у этих уравнений есть своя очень важная «ниша» в физике.
Вспомним: если сказано, что некоторые величины x, y, y′, y′′,... участвуют в некотором выражении F «линейно», то это значит, что эти величины входят в выражение только в «первой степени».
| Определение: (1.1) | Дифференциальное уравнение 1-го порядка F (x, y, y′)=0 называют линейным, если входящие в него независимая переменная x, искомую функцию y и ее производная y′ входят в уравнение в 1-й степени. Запись линейного уравнения считаем «стандартной, если она имеет вид»: y′ + P (x)∙ y = Q (x), (1) где P (x) и Q (x) – непрерывные функции от х или постоянные. |
Замечание: Свойства P (x) и Q (x) обеспечивают выполнение требований Теоремы «о существовании и единственности решения...».
|
|
|
Способов решения уравнения (1) – можно было бы рассмотреть несколько. Здесь мы рассмотрим только способ «подстановки». В пособии будет рассмотрен ещё способ «вариации произвольной постоянной», который считаем также обязательным при изучении настоящего курса «Дифференциальные уравнения».
Способ подстановки. Кто-то «догадался», что решение возможно в форме:
y = u (x)∙ v (x). (2)
Далее следует применить уже отработанную «технологию»: подставить эту функцию и её производную в уравнение (1) и «потребовать» превращения уравнения в тождество! Если такое возможно при выделении реализуемых требований, значит способ «срабатывает». Итак, выполним действия:
▪ вычислим производную: y′ = u′ ∙ v + u ∙ v′;
▪ подставим: функцию y = u ∙ v и её производную y′ = u′ ∙ v + u ∙ v′ в уравнение (1):
u′ ∙ v + u ∙ v′ + P (x)∙ u ∙ v = Q (x) → u ∙ v′ + v ∙(u′ + P (x)∙ u) = Q (x). (3)
Так как функции u и v пока не ограничены в свойствах, то «потребуем» от функции u (x) выполнения свойства: u′ + P (x)∙ u =0 или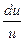 
= – P (x)∙ dx. (4)
Уравнение (4) есть уравнение с разделяющимися переменными. Его решение можно записать в виде: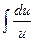 
= –
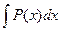→ u =
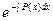. (5)
Замечание: При интегрировании уравнения (4) не применяется произвольная постоянная, так как важно только одно свойство функции u (x): обнулить одно слагаемое в уравнении (3). Понятно, требования к функции v (x) должны обеспечить решение задачи Коши, то есть содержать произвольную постоянную!
|
|
|
Теперь из уравнения (3) имеем: u ∙ v′ = Q (x) или dv =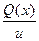
dx. (6)
Уравнение (6) есть уравнение с разделёнными переменными. Его решение можно записать в виде: v =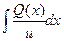 
+С. (7)
Условия (5) и (7) обеспечивают для y = u ∙ v свойство быть решением уравнения (1). Теперь решение (2) принимает вид: y =∙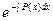
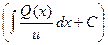. (8)
Замечание: При решении конкретного линейного дифференциального уравнения необходимо использовать готовый результат в виде формулы (8), а не «выводить» её каждый раз заново!
