Тема: применение языка логики предикатов для записи математических предложений, определений, построения отрицания предложений

Лекция 13

ПЛАН:

1. Запись математических предложений в виде формул логики предикатов.

2. Построение противоположных утверждений.

3. Прямая, обратная и противоположные теоремы.

4. Необходимые и достаточные условия.

5. Доказательство методом от противного.

Главная

 

1. Запись математических предложений в виде формул логики предикатов.

Язык логики предикатов удобен для записи матема­тических предложений. Он дает возможность выражать логические связи между понятиями, записывать опреде­ления, теоремы, доказательства. Приведем ряд приме­ров таких записей.

1) Определение предела числовой последовательности.

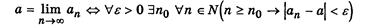
Здесь использован трехместный предикат Q(e,n,n_o):

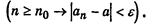
2). Определение предела функции в точке.

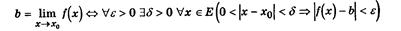
Здесь использован трехместный предикат Р(e,d,х):

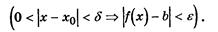
3). Определение непрерывности функции в точке.

Функция f(x), определенная на множестве Е, непре­рывна в точке х₀ Î Е, если

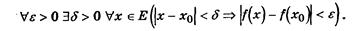
Здесь также использован трехместный предикат Р(e,d,х).

4). Определение возрастающей функции.

Функция f(x), определенная на множестве Е, возра­стает на этом множестве, если

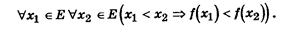
Здесь использован двухместный предикат B(x₁, x₂):

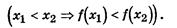
5). Определение ограниченной функции.

Функция f(х), определенная на множестве Е, огра­ничена на этом множестве, если

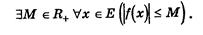
Здесь использован двухместный предикат L(x,M):(|f(x)|£M).

Как известно, многие теоремы математики допускают формулировку в виде условных предложений. Например, рассмотрим следующую теорему: «Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла». Условием этой теоремы является предложение «Точка лежит на биссектрисе угла», а заключением – предложение «Точка равноудалена от сторон угла». Видим, что и усло­вие, и заключение теоремы представляют собой предика­ты, заданные на множествеR². Обозначая эти предикаты

соответственно через Р(х) и Q(x), где х Î R², теорему можем записать в виде формулы:

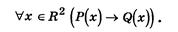
В связи с этим, говоря о строении теоремы, можно выделить в ней три части:1) условие теоремы: предикат Р(х), заданный на множестве R²; 2) заключение теоре­мы: предикат Q(x), заданный на множестве R²; 3) разъяс­нительная часть: в ней описывается множество объек­тов, о которых идет речь в теореме.

 

2. Построение противоположных утверждений.

Пусть дано некоторое математическое утверждение А. Ему противоположным будет утверждение .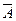

Логика предикатов позволяет путем равносильных преобразований формулы 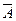придать ей хорошо обозри­мый вид.

Так, например, определение ограниченной функции дается формулой:

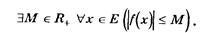
Определение неограниченной функции мы получим, беря отрицание этой формулы и проводя равносильные пре­образования:

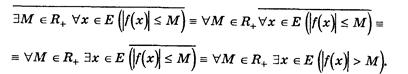
Последняя формула дает не негативное, а положитель­ное определение неограниченной функции.

Из приведенного определения видно, что для постро­ения противоположного утверждения к утверждению, заданному формулой логики предикатов, содержащей все кванторы впереди, необходимо заменить все кванторы на противоположные и взять отрицание от предиката, стоящего под знаком кванторов.

Так, утверждение, что 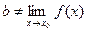даст формула:

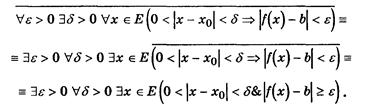
Особый интерес представляет построение утвержде­ния, отрицающего справедливость некоторой теоремы: "хÎE(P(x)®Q(x)).

Это будет утверждение:

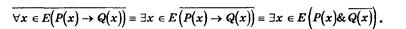
Следовательно, чтобы доказать, что теорема "хÎE(P(x)®Q(x)) неверна, достаточно указать такой эле­мент х Î Е, для которого Р(х) - истина, a Q(x) - ложь, то есть привести контрпример.

Используя данный прием докажем несправедливость утверждений:

1. «Если дифференцируемая функция y = f(x) имеет в точке х₀ производную, равную нулю (y’=0), то то точка х₀ – точка экстремума.» достаточно указать один пример, опровергающий утверждение теоремы. Функция y = x³ в точке х=0 имеет производную у’=3х² = 0, но эта точка не является точкой экстремума. Значит, теорема не верна.
2. «Если в четырехугольнике диагонали равны, то четырехугольник является параллелограммом.» В качестве контрпримера можно привести равнобокую трапецию, у которой диагонали равны, но она не является прямоугольником.

 

3. Прямая, обратная и противоположная теоремы.

Рассмотрим четыре теоремы:

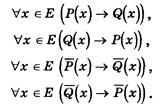
Пара теорем, у которых условие одной является зак­лючением второй, а условие второй является заключени­ем первой, называются взаимно обратными друг другу.

Так, теоремы (1) и (2), а также (3) и (4) - взаимно обратные теоремы. При этом, если одну из них называ­ют прямой теоремой, то вторая называется обратной.

Пара теорем, у которых условие и заключение одной является отрицанием соответственно условия и заключе­ния другой, называются взаимно противоположными.

Так, теоремы(1) и (3), а также теоремы (2) и (4)являются взаимно противоположными теоремами.

Например, для теоремы «Если в четырехугольнике диагонали равны, то четырехугольник является прямоу­гольником» (1) обратной является теорема «Если четы­рехугольник является прямоугольником, то его диаго­нали равны» (2). Для теоремы (1) противоположной яв­ляется теорема «Если в четырехугольнике диагонали не равны, то четырехугольник не является прямоугольни­ком» (3), а для теоремы (2) противоположной является теорема «Если четырехугольник не является прямоуголь­ником, то его диагонали не равны» (4).

В рассмотренном примере теоремы (1) и (4) являют­ся одновременно ложными, а теоремы (2) и (3) одновре­менно истинными. Контрпримером к теореме (1) являет­ся равнобокая трапеция.

Ясно, что прямая и обратная теоремы, вообще гово­ря, не равносильны, то есть одна из них может быть истинной, а другая ложной. Однако легко показать, что теоремы (1) и (4), а также теоремы (2) и (3) всегда равно­сильны. Действительно,

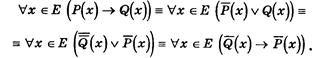
Аналогично доказывается равносильность

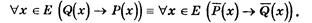
Из этих равносильностей следует, что, если доказа­на теорема(1), то доказана и теорема (4), а если доказа­на теорема (2), то доказана и теорема(3).