Экстраполяция – распространение результатов, полученных из наблюдения над одной частью эксперимента, на другую его часть. Так, если известны значения функции y =f (x) на отрезке [ a, b ], то по ее значениям в точках x0 ,x1 ,…, xn (x0 < x1 < …< xn) можно определить значение функции в точках, лежащих вне отрезка [ a, b ].
Аппаратом для этого служит, например, параболическая экстраполяция, при которой в качестве значения f (x) в точке x берется значение многочлена Pn (x) степени n, принимающего в n +1 точке xi заданные значения yi =f (xi).
Для параболической экстраполяции используются обычные интерполяционные формулы, например формула Ньютона для равностоящих точек xi = x0 + t h:
Pn (xn + t h) = yn + 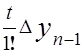 +
+ 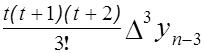 + … + +
+ … + +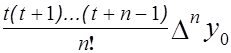 ,
,
где 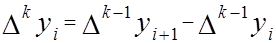 .
.
Например, если для функции y =f (x) составлен ряд частных значений y0 , y1 , …, yn, соответствующих a, a + h, …, a + n h, то
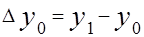 ,
,
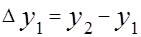 ,
,
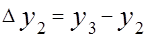
и
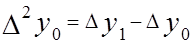 ,
,
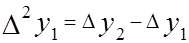 ,
,
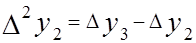 и т.д.
и т.д.
Наконец,
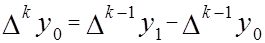 ,
,
…
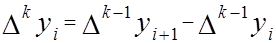 ,
,
где 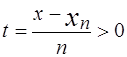 и x > xn.
и x > xn.
Погрешность, совершаемая при вычислении по этой формуле значения f (x) в точке xi = x0 + t h, не превышает
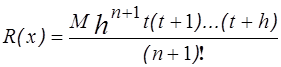 ,
,
где M - максимум абсолютного значения n + 1-й производной f (x) на отрезке [ a, b ].
|
|
|
 2014-02-09
2014-02-09 3348
3348








