Если через точку М(x 0, y 0, z 0 ) некоторой поверхности S провести всевозможные кривые и к ним в этой точке провести касательные прямые, то окажется, что все эти касательные лежат в одной плоскости, которая называется касательной плоскостью к поверхности S в точке М, а перпендикуляр к касательной плоскости, восстановленный к ней в точке касания М, называется нормалью к поверхности.
Пусть поверхность задана уравнением 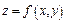 , где
, где 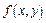 - дифференцируемая функция, тогда уравнение касательной плоскости в точке М( x 0, y 0, z 0 ) поверхности S есть
- дифференцируемая функция, тогда уравнение касательной плоскости в точке М( x 0, y 0, z 0 ) поверхности S есть 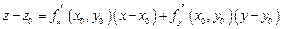 , (2)
, (2)
а уравнение нормали к поверхности в точке 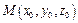 :
: 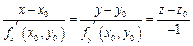 . (3)
. (3)
Пример 5. Составить уравнение касательной плоскости и нормали к поверхности 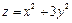 в точке
в точке 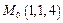 .
.
Решение:
1). Проверим, принадлежит ли точка М 0поверхности 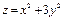 . Для этого подставим ее координаты в уравнение этой поверхности. В результате получится верное равенство. Следовательно, точка
. Для этого подставим ее координаты в уравнение этой поверхности. В результате получится верное равенство. Следовательно, точка  принадлежит поверхности
принадлежит поверхности 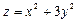 .
.
2). Определим частные производные первого порядка и вычислим их значения в точке касания:
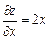 ,
, 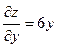 ,
, 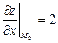 ,
, 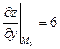 .
.
3). Так как поверхность задана в явном виде, то уравнение касательной плоскости будет иметь вид (2): 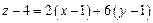 или
или 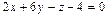 .
.
|
|
|
4). Уравнение нормали запишется в виде (3): 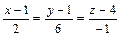 .
.
 2015-01-30
2015-01-30 1283
1283








