Механическая система состоит из грузов 1 и 2 (коэффициент трения грузов о плоскость f = 0,1), сплошного однородного цилиндрического катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней: R4 = 0,3 м, r4 = 0,1 м, R5 = 0,2 м, r5 = 0,1 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу) (схемы
0 – 9). Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям.
Под действием силы F = f (s), зависящей от перемещения точки приложения силы, система приходит в движениеиз состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивлений, равные соответственно М4 и M5.
Варианты схем к задаче 3
0) 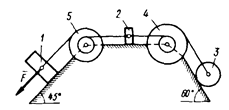 2) 2) 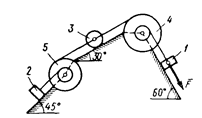 4) 4) 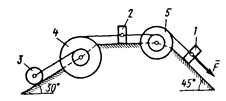 6) 6) 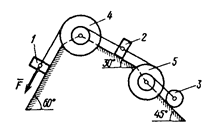 8) 8) 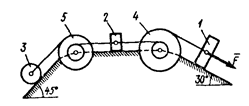 | 1) 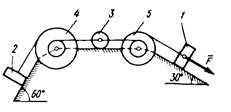 3) 3) 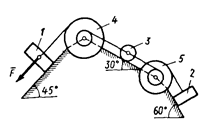 5) 5) 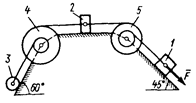 7) 7) 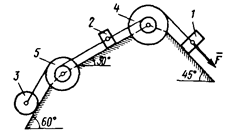 9) 9) 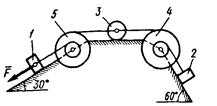 |
Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы 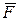 равно s1. Искомая величина указана в табл. 7.8, где обозначено v1 – скорость груза 1, vC3 – скорость центра масс катка 3, ω4 – угловая скорость тела 4 и т.д.
равно s1. Искомая величина указана в табл. 7.8, где обозначено v1 – скорость груза 1, vC3 – скорость центра масс катка 3, ω4 – угловая скорость тела 4 и т.д.
Таблица 7.8
| Номер варианта условий | m1, кг | m2, кг | т3, кг | m4, кг | m5, кг | М4, Н м | M5, Н м | F = f(s), Н | s1 м | Найти |
| 0,8 | 50 (2 + 3 s) | 1,0 | v1 | |||||||
| 0,6 | 20 (5 + 2 s) | 1,2 | ω5 | |||||||
| 0,4 | 80(3 + 4s) | 0,8 | vC3 | |||||||
| 0,3 | 40(4 + 5 s) | 0,6 | v2 | |||||||
| 0,6 | 30(3 + 2 s) | 1,4 | ω4 | |||||||
| 0,9 | 40(3+5 s) | 1,6 | v1 | |||||||
| 0,8 | 60(2 + 5 s) | 1,0 | ω4 | |||||||
| 0,6 | 30 (8 + 3 s) | 0,8 | ω5 | |||||||
| 0,3 | 40(2 + 5 s) | 1,6 | vC3 | |||||||
| 0,4 | 50(3 + 2 s) | 1,4 | v2 |
Указания. Это задача на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел. Эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении кинетической энергии катка, движущегося плоскопараллельно, для установления зависимости между его угловой скоростью и скоростью его центра масс воспользоваться понятием о мгновенном центре скоростей (кинематика). При определении работы все перемещения следует выразить через заданное перемещение s1, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями
Когда по данным табл. 7.8 m2 = 0, груз 2 на чертеже не изображать, шкивы 4 и 5 всегда входят в систему.
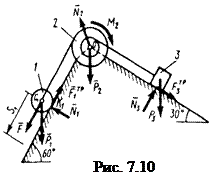 Пример решения задачи 3
Пример решения задачи 3
Механическая система (рис. 7.10) состоит из сплошного цилиндрического катка 1, ступенчатого шкива 2 с радиусами ступеней R2 и r2, (масса шкива равномерно распределена по его внешнему ободу) и груза 3 (коэффициент трения груза о плоскость равен f). Тела системы соединены друг с другом нитями, намотанными на шкив 2.
Под действием силы F = f (s),зависящей от перемещения (s) точки ее приложения, система приходит в движения из состояния покоя. При движении на шкив 2 действует постоянный момент (М2) cил сопротивления.
Дано: т1 = 4 кг; т2 = 10 кг; т3 = 8 кг; R2 = 0,2 м; r2 = 0,1 м; f = 02;
М2 = 0,6 Нּм; F = 2 (1 + 2 s); s1 = 2 м.
Определить скорость vC1, центра масс катка, когда s = s1.
 2015-01-30
2015-01-30 5383
5383








