При исследовании социально-экономических явлений часто приходится иметь дело с взаимосвязанными показателями. При этом часто связь, существующая между двумя или несколькими показателями, усложняется, так как на их взаимодействие оказывает множество факторов. Изучить, насколько изменение одного показателя зависит от изменения другого (или нескольких), - одна из важнейших задач статистики.
Следует различать функциональные и корреляционные связи. При функциональной зависимости каждому значению одной переменной строго соответствует определенное значение другой. Зависимость, при которой одному значению переменной 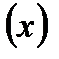 может соответствовать множество значений другой переменной
может соответствовать множество значений другой переменной 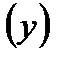 , называют корреляционной. Корреляционная зависимость проявляется лишь на основе массового наблюдения. Например, зависимость производительности труда от стажа работы.
, называют корреляционной. Корреляционная зависимость проявляется лишь на основе массового наблюдения. Например, зависимость производительности труда от стажа работы.
Наиболее простым случаем корреляционной зависимости является парная корреляция, то есть зависимость между двумя признаками (результативным и одним из факторных).
|
|
|
Основными задачами при изучении корреляционных зависимостей являются:
1) выявление формы связи в виде математической формулы, выражающей эту зависимость у от х;
2) измерение тесноты такой зависимости.
Решение первой задачи, то есть определение формы связи с последующим отысканием параметров уравнения, называется нахождением уравнения связи (уравнения регрессии). Результативный показатель, рассматриваемый как функция 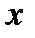 , обозначает
, обозначает 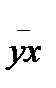
Возможны различные формы связи:
1) прямолинейная: 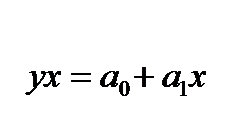 ; (77)
; (77)
2) криволинейная в виде:
– параболы второго порядка 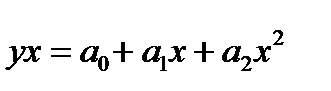 ; (78)
; (78)
– гиперболы 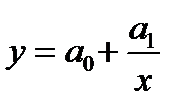 ; (79)
; (79)
– показательной функции 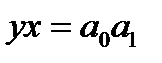 . (80)
. (80)
Параметры для всех уравнений связи чаще всего определяют системой нормальных уравнений, отвечающих требованию метода наименьших квадратов. Это требование можно записать:
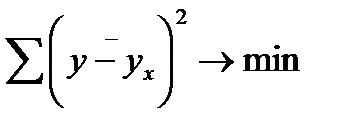 (81)
(81)
или при линейной зависимости
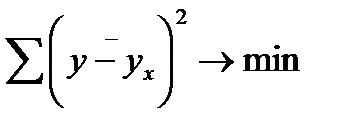 (82)
(82)
То есть требуется, определить при каких значениях параметров 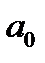 и
и 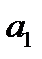 , сумма квадратов отклонений
, сумма квадратов отклонений 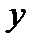 от
от 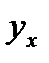 будет минимальной. Найдя частные производные указанной суммы по
будет минимальной. Найдя частные производные указанной суммы по 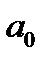 и
и 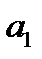 и приравняв их к нулю, легко записать систему уравнений, решение которой и дает параметры искомой функции, то есть уравнения регрессии.
и приравняв их к нулю, легко записать систему уравнений, решение которой и дает параметры искомой функции, то есть уравнения регрессии.
Система нормальных уравнений при линейной зависимости имеет вид:
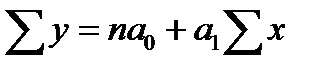 ; (83)
; (83)
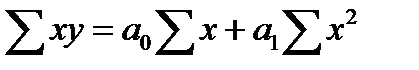 .
.
Необходимые для решения данной системы показатели 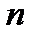 ,
, 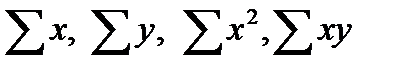 определяются по наблюдаемым эмпирическим данным. Решить такую систему нормальных уравнений можно разными способами.
определяются по наблюдаемым эмпирическим данным. Решить такую систему нормальных уравнений можно разными способами.
Для нахождения 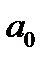 и
и 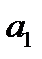 при линейной зависимости можно воспользоваться формулами:
при линейной зависимости можно воспользоваться формулами:
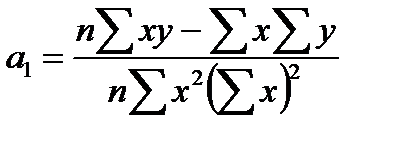 (84)
(84)
или
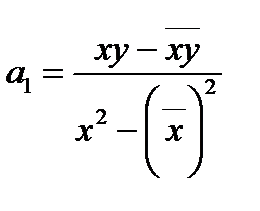 . (85)
. (85)
Параметр 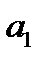 – коэффициент при х – именуемый коэффициентом регрессии. Он показывает, на сколько в абсолютном выражении изменится результативный показатель
– коэффициент при х – именуемый коэффициентом регрессии. Он показывает, на сколько в абсолютном выражении изменится результативный показатель 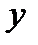 при изменении факторного показателя
при изменении факторного показателя 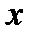 на единицу.
на единицу.
|
|
|
Зная 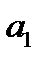 , легко определить второй параметр уравнения регрессии:
, легко определить второй параметр уравнения регрессии:
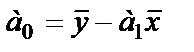 (86)
(86)
Если связь выражена параболой второго порядка:
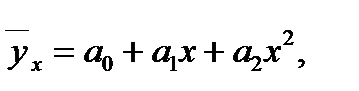 (87)
(87)
Нахождение уравнений регрессии сопровождается измерением тесноты связи (зависимости).
Измерить тесноту корреляционной зависимости - значит определить, насколько (в какой мере) вариация результативного показателя вызвана вариацией факторного признака.
Для оценки тесноты связи в статистическом анализе используют показатели:
эмпирического корреляционного отношения (ηэ):
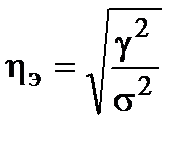 , (88)
, (88)
где 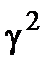 – межгрупповая вариация результативного признака;
– межгрупповая вариация результативного признака;
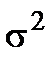 – общая вариация результативного признака.
– общая вариация результативного признака.
Наличие взаимосвязей между результативным и факторным признаком имеет при η ≤ 0,5.
Универсальным показателем тесноты связи является показатель теоретического корреляционного отношения или индекс корреляции (ηm):
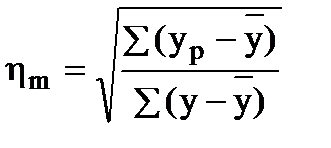 , (89)
, (89)
где 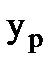 – рассчитанные (теоретические) значения результативного признака.
– рассчитанные (теоретические) значения результативного признака.
Показатель теоретического корреляционного отношения может использоваться для оценки тесноты связи не только в парных, но и многофакторных зависимостей.
Для оценки тесноты связи прямолинейной зависимости используется линейный коэффициент корреляции (r):
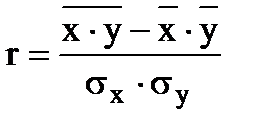 (90)
(90)
или
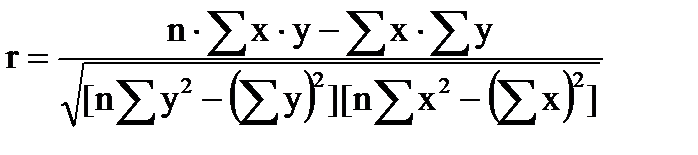 . (91)
. (91)
Линейный коэффициент корреляции может изменяться от -1 до +1. Чем ближе значение r по абсолютной величине к единице, тем теснее связь. Если r>0, то связь между факторным и результативным признаками прямо пропорциональная, если r<0, то обратно пропорциональная.
Для предварительной оценки тесноты связи корреляции может использоваться коэффициент корреляции знаков (коэффициент Г. Фехнера).
Для определения коэффициента знаков Г. Фехнера вычисляются средние значения факторного и результативного признаков, затем определяются знаки отклонений от средней всех значений взаимосвязанных признаков. Приняв число совпадений знаков отклонений индивидуальных значений от средней за «С», а число несовпадений за «Н», коэффициент определяется следующим образом:
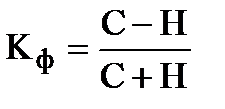 . (92)
. (92)
Коэффициент Г. Фехнера может принимать значения от
-1 до +1; если он положительный, то связь между признаками признается прямой, если отрицательный, то обратной.
Рассмотренные выше показатели корреляции приемлемы лишь для условий нормального или близкого к нормальному распределения и только для количественных признаков. Если эти условия отсутствуют и к тому же исследуются атрибутивные признаки, то приходится пользоваться непараметрическими методами корреляционного анализа, в частности - корреляцией рангов или ранговой корреляцией. Ранг признака (Ri) указывает то место, которое занимает i-й признак среди других n-признаков в ранжированном ряду распределения.
Если одно и то же значение признака в ранжированном ряду распределения занимает разные порядковые номера, то ранг признака определяется по сопряженному рангу (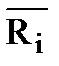 ), рассчитанному как среднее арифметическое порядковых номеров, занимаемых данным признаком.
), рассчитанному как среднее арифметическое порядковых номеров, занимаемых данным признаком.
Для такого рода ранжированных признаков показателями тесноты связи служат коэффициенты корреляции рангов К. Спирмэна (ρ) и М. Кендэла (τ).
Коэффициент корреляции К. Спирмэна (ρ) определяется по формуле:
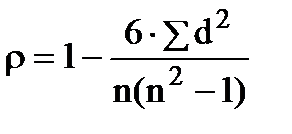 , (93)
, (93)
где n – число сопоставимых пар;
d – разность между рангами коррелирующих признаков (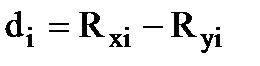 ).
).
Этот коэффициент интерпретируется также, как и линейный коэффициент корреляции, имеет те же свойства и пределы значений (от -1 до +1).
Коэффициент корреляции М. Кендэла (τ) определяется по формуле:
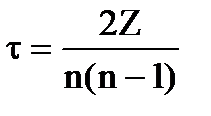 , (94)
, (94)
где Z – алгебраическая сумма числа высших (P) и низших (Q) рангов по отношению к каждому последующему рангу y, сопоставленному в строгом соответствии с рядом значений х в восходящем или нисходящем порядках, т.е. Z=P-Q.
|
|
|
Расчет данного коэффициента выполняется в следующем порядке:
1. Значения признака х выстраиваются в строчной последовательности возрастания или убывания.
2. Значения у располагаются в порядке, соответствующем значениям х.
3. Для каждого ранга у определяется число следующих за ним значений рангов, превышающих его величину. Суммируя эти числа, определяется величина Р как мера соответствия последовательностей рангов х и у.
4. Для каждого ранга у определяется число следующих за ним значений рангов, меньших его величины. Суммарная величина этих чисел обозначается Q.
Как правило, коэффициент Кендэла меньше коэффициента Спирмэна:
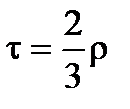 . (95)
. (95)
Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации)  , который вычисляется по формуле:
, который вычисляется по формуле:
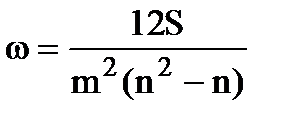 , (96)
, (96)
где m – количество факторов;
S – отклонение суммы квадратов рангов от средней квадратов рангов:
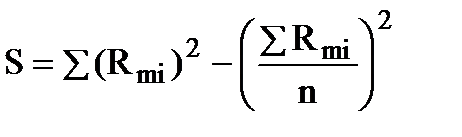 . (97)
. (97)
Связь между признаками признается значимой, если значение коэффициентов корреляции рангов больше 0,5.
Для оценки тесноты связей между атрибутивными признаками, помимо коэффициентов ранговой корреляции, могут применяться специальные коэффициенты.
 2015-01-30
2015-01-30 856
856








