Метод проекций

ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ

Начертательная геометрия является одной из фундаментальных наук, составляющих основу инженерно-технического образования. Она изучает методы изображения пространственных геометрических фигур на плоскости и способы решения метрических и позиционных задач в пространстве по этим изображениям.

МЕТОД ПРОЕКЦИЙ

Под проецированием подразумевается процесс, в результате которого получаются изображения – проекции на плоскости.

Основными элементами проецирования являются:

1. Проецируемый объект (точка А).

2. Плоскость проекций (плоскость П₁).

3. Центр проецирования S.

4. Проецирующий луч i.

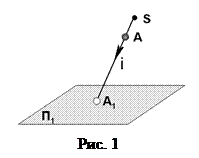
Проецирующий луч (рис.1) выходит из центра проецирования S через точку А до пересечения с плоскостью П₁. Точка пересечения А₁ является проекцией точки А.

А₁ = i Ç П₁

Если центр проецирования находится на определенном расстоянии от плоскости проекций (рис.2), то такое проецирование называется центральным.

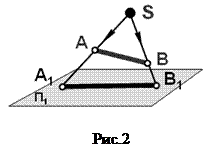
Полученное изображение дает представление только о форме предмета, но не о его размерах, т.к. изображение получается увеличенным. Центральное проецирование применяют для изображения предметов в перспективе.

Если центр проецирования удален в бесконечность (рис.3), то все проецирующие лучи становятся параллельными и проецирование называется параллельным.

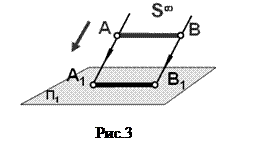В зависимости от направления проецирования к плоскости проекций параллельное проецирование разделяют на косоугольное и прямоугольное (ортогональное).

Если угол наклона проецирующего луча к плоскости проекций меньше 90⁰, то проецирование называется косоугольным (рис.4).

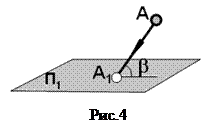
Если проецирующий луч перпендикулярен плоскости проекций, то проецирование называется ортогональным (рис.5).

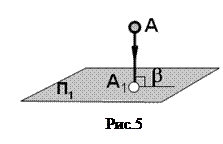Этот метод широко используется при составлении чертежей, т.к. имеет ряд преимуществ перед центральным и косоугольным параллельным проецированием. К ним относятся простота геометрических построений ортогональных проекций точек и сохранение на проекциях, при определенных условиях, формы и размеров проецируемой фигуры.

ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ

Геометрические фигуры в общем случае проецируются на плоскость проекций с искажением. Проекции не сохраняют линейные и угловые величины оригинала. Характер этих искажений зависит от положения геометрической фигуры в пространстве и от аппарата проецирования.

Однако некоторые свойства фигур остаются неизменными в процессе проецирования. Такие свойства называются независимыми или инвариантными для данного аппарата проецирования.

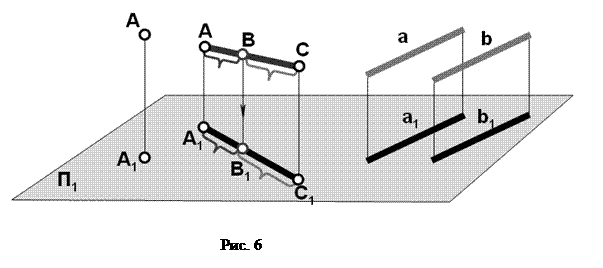
1. Проекция точки есть точка (рис.6).

2. Проекция прямой есть прямая (в общем случае).

3. Если точка принадлежит прямой, то и проекция точки принадлежит проекции прямой.

ВÎ[АС] Þ В₁Î [ А₁С₁]

4. Отношение отрезков прямой равно отношению проекций этих отрезков.

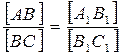
5. Если прямые параллельны, то и их проекции параллельны между собой.

А½½b Þ a₁½½b₁

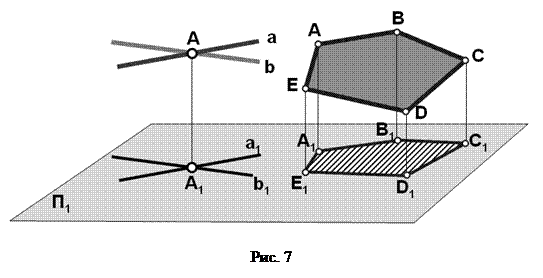
6. Проекция точки пересечения прямых есть точка пересечения проекций этих прямых (рис.7).

7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.