Тангенциальная составляющая ускорения 24 страница

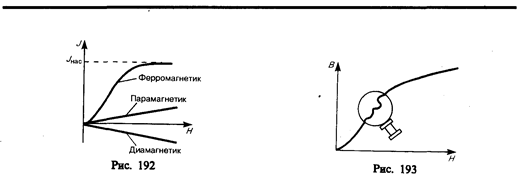
Различные ферромагнетики дают разные гистерезисные петли. Ферромагнетики с малой (в пределах от нескольких тысячных до 1—2 А/см) коэрцитивной силой Нс (с узкой петлей гистерезиса) называются мягкими, с большой (от нескольких десятков до нескольких тысяч ампер на сантиметр) коэрцитивной силой (с широкой петлей гистерезиса) — жесткими. Величины Нс, J _ос и m _max определяют применимость фер­ромагнетиков для тех или иных практических целей. Taк, жесткие ферромагнетики (например, углеродистые и вольфрамовые стали) применяются для изготовления постоянных магнитов, а мягкие (например, мягкое железо, сплав железа с нике­лем) — для изготовления сердечников трансформаторов.

Ферромагнетики обладают еще одной существенной особенностью: для каждого ферромагнетика имеется определенная температура, называемая точкой Кюри, при которой он теряет свои магнитные свойства. При нагревании образца выше точки Кюри ферромагнетик превращается в обычный парамагнетик. Переход вещества из ферромагнитного состояния в парамагнитное, происходящий в точке Кюри, не со­провождается поглощением или выделением теплоты, т.е. в точке Кюри происходит фазовый переход II рода (см. § 75).

Наконец, процесс намагничения ферромагнетиков сопровождается изменением его линейных размеров и объема. Это явление получило название магнитострикции. Величина и знак эффекта зависят от напряженности Н намагничивающего поля, от природы ферромагнетика и ориентации кристаллографических осей по отношению к полю.

§ 136. Природа ферромагнетизма

Рассматривая магнитные свойства ферромагнетиков, мы не вскрывали физическую природу этого явления. Описательная теория ферромагнетизма была разработана французским физиком П. Вейссом (1865—1940). Последовательная количественная теория на основе квантовой механики развита Я. И. Френкелем и немецким физиком В. Гейзенбергом (1901—1976).

Согласно представлениям Вейсса, ферромагнетики при температурах ниже точки Кюри обладают спонтанной намагниченностью независимо от наличия внешнего намагничивающего поля. Спонтанное намагничение, однако, находится в кажущемся противоречии с тем, что многие ферромагнитные материалы даже при температурах ниже точки Кюри не намагничены. Для устранения этого противоречия Вейсс ввел гипотезу, согласно которой ферромагнетик ниже точки Кюри разбивается на большое число малых макроскопических областей — доменов, самопроизвольно намагниченных до насыщения.

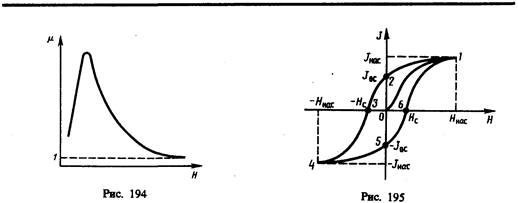
При отсутствии внешнего магнитного поля магнитные моменты отдельных до­менов ориентированы хаотически и компенсируют друг друга, поэтому результиру­ющий магнитный момент ферромагнетика равен нулю и ферромагнетик не намаг­ничен. Внешнее магнитное поле ориентирует по полю магнитные моменты не отдель­ных атомов, как это имеет место в случае парамагнетиков, а целых областей спонтан­ной намагниченности. Поэтому с ростом Н намагниченность J (см. рис. 192) и магнит­ная индукции В (см. рис. 193) уже в довольно слабых полях растут очень быстро. Этим объясняется также увеличение m ферромагнетиков до максимального значения в слабых полях (см. рис. 194). Эксперименты показали, что зависимость B от H не является такой плавной, а имеет ступенчатый вид, как показано на рис. 193. Это свидетельствует о том, что внутри ферромагнетика домены поворачиваются по полю скачком.

При ослаблении внешнего магнитного поля до нуля ферромагнетики сохраняют остаточное намагничение, так как тепловое движение не в состоянии быстро дезориен­тировать магнитные моменты столь крупных образований, какими являются домены. Поэтому и наблюдается явление магнитного гистерезиса (рис. 195). Для того чтобы ферромагнетик размагнитить, необходимо приложить коэрцитивную силу; размаг­ничиванию способствуют также встряхивание и нагревание ферромагнетика. Точка Кюри оказывается той температурой, выше которой происходит разрушение доменной структуры.

Существование доменов в ферромагнетиках доказано экспериментально. Прямым экспериментальным методом их наблюдения является метод порошковых фигур. На тщательно отполированную поверхность ферромагнетика наносится водная суспензия мелкого ферромагнитного порошка (например, магнетита). Частицы оседают преиму­щественно в местах максимальной неоднородности магнитного поля, т. е. на границах между доменами. Поэтому осевший порошок очерчивает границы доменов и подобную картину можно сфотографировать под микроскопом. Линейные размеры доменов оказались равными 10^–4 — 10^–2 см.

Дальнейшее развитие теории ферромагнетизма Френкелем и Гейзенбергом, а также ряд экспериментальных фактов позволили выяснить природу элементарных носителей ферромагнетизма. В настоящее время установлено, что магнитные свойства ферромагнетиков определяются спиновыми магнитными моментами элект­ронов (прямым экспериментальным указанием этого служит опыт Эйнштейна и де Гааза, см. § 131). Установлено также, что ферромагнитными свойствами могут обладать только кристаллические вещества, в атомах которых имеются недостроен­ные внутренние электронные оболочки с нескомпенсированными спинами. В подо­бных кристаллах могут возникать силы, которые вынуждают спиновые магнитные моменты электронов ориентироваться параллельно друг другу, что и приводит к возникновению областей спонтанного намагничения. Эти силы, называемые обменными силами, имеют квантовую природу — они обусловлены волновыми свойствами электронов.

Так как ферромагнетизм наблюдается только в кристаллах, а они обладают анизотропией (см. § 70), то в монокристаллах ферромагнетиков должна иметь место анизотропия магнитных свойств (их зависимость от направления в кристалле). Дейст­вительно, опыт показывает, что в одних направлениях в кристалле его намагничен­ность при данном значении напряженности магнитного поля наибольшая (направление легчайшего намагничения), в других — наименьшая (направление трудного намагничения). Из рассмотрения магнитных свойств ферромагнетиков следует, что они похожи на сегнетоэлектрики (см. § 91).

Существуют вещества, в которых обменные силы вызывают антипараллельную ориентацию спиновых магнитных моментов электронов. Такие тела называются антиферромагнетиками. Их существование теоретически было предсказано Л.Д. Лан­дау. Антиферромагнетиками являются некоторые соединения марганца (MnO, MnF₂), железа (FeO, FeCl₂) и многих других элементов. Для них также существует антиферромагнитная точка Кюри (точка Нееля*), при которой магнитное упорядочение спиновых магнитных моментов нарушается и антиферромагнетик превращается в парамагнетик, претерпевая фазовый переход II рода (см. § 75).

* Л. Неель (род. 1904) — французский физик.

В последнее время большое значение приобрели полупроводниковые ферромаг­нетики — ферриты, химические соединения типа МeО×Fе₂О₃, где Me — ион двухва­лентного металла (Mn, Co, Ni, Сu, Mg, Zn, Cd, Fe). Они отличаются заметными ферромагнитными свойствами и большим удельным электрическим сопротивлением (в миллиарды раз большим, чем у металлов). Ферриты применяются для изготовления постоянных магнитов, ферритовых антенн, сердечников радиочастотных контуров, элементов оперативной памяти в вычислительной технике, для покрытия пленок в магнитофонах и видеомагнитофонах и т. д.

Задачи

16.1. Напряженность однородного магнитного поля в меди равна 10 А/м. Определить магнитную индукцию поля, создаваемого молекулярными токами, если диамагнитная восприимчи­вость меди |c|=8,8×10^–8. [1.11 пТл]

16.2. По круговому контуру радиусом 50 см, погруженному в жидкий кислород, течет ток 1,5 А. Определить намагниченность в центре этого контура, если магнитная восприимчивость жидкого кислорода 3,4×10^–3. [5,1 мА/м]

16.3. По обмотке соленоида индуктивностью 1 мГн, находящегося в диамагнитной среде, течет ток 2 А. Соленоид имеет длину 20 см, площадь поперечного сечения 10 см² и 400 витков. Определить внутри соленоида: 1) магнитную индукцию; 2) намагниченность. [1) 5 мТл; 2) 20 А/м]

16.4. Алюминиевый шарик радиусом 0,5 см помещен в однородное магнитное поле (B ₀ = 1 Тл). Определить магнитный момент, приобретенный шариком, если магнитная восприимчи­вость алюминия 2,1×10^–5. [8,75 мкА×м²]

Глава 17 Основы теории Максвелла для электромагнитного поля

§ 137. Вихревое электрическое поле

Из закона Фарадея (см. (123.2)) 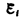=–dФ/d t следует, что любое изменение сцепленного с контуром потока магнитной индукции приводит к возникновению электродвижущей силы индукции и вследствие этого появляется индукционный ток. Следовательно, возникновение э.д.с. электромагнитной индукции возможно и в неподвижном контуре,находящемся в переменном магнитном поле. Однако э.д.с. в любой цепи возникает только тогда, когда в ней на носители тока действуют сторонние силы — силы неэлектростатического происхождения (см. § 97). Поэтому встает вопрос о природе сторонних сил в данном случае.

Опыт показывает, что эти сторонние силы не связаны ни с тепловыми, ни с хи­мическими процессами в контуре; их возникновение также нельзя объяснить силами Лоренца, так как они на неподвижные заряды не действуют. Максвелл высказал гипотезу, что всякое переменное магнитное поле возбуждает в окружающем простран­стве электрическое поле, которое и является причиной возникновения индукционного тока в контуре. Согласно представлениям Максвелла, контур, в котором появляется э.д.с., играет второстепенную роль, являясь своего рода лишь «прибором», обнаружи­вающим это поле.

Итак, по Максвеллу, изменяющееся во времени магнитное поле порождает элект­рическое поле Е _B, циркуляция которого, по (123.3),

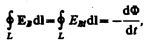(137.1)

где Е_Bl — проекция вектора Е _B на направление d l.

Подставив в формулу (137.1) выражение 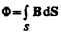(см. (120.2)), получим

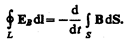
Если поверхность и контур неподвижны, то операции дифференцирования и интег­рирования можно поменять местами. Следовательно,

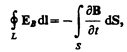(137.2)

где символ частной производной подчеркивает тот факт, что интеграл 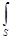B d S является функцией только от времени.

Согласно (83.3), циркуляция вектора напряженности электростатического поля (обозначим его E _Q) вдоль любого замкнутого контура равна нулю:

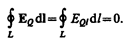(137.3)

Сравнивая выражения (137.1) и (137.3), видим, что между рассматриваемыми полями (E _B и Е _Q) имеется принципиальное различие: циркуляция вектора E _B в отличие от циркуляции вектора E _Q не равна нулю. Следовательно, электрическое поле E _B, возбуж­даемое магнитным полем, как и само магнитное поле (см. § 118), является вихревым.

§ 138. Ток смещения

Согласно Максвеллу, если всякое переменное магнитное поле возбуждает в окружа­ющем пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля. Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнит­ным полем Максвелл ввел в рассмотрение так называемый ток смещения.

Рассмотрим цепь переменного тока, содержащую конденсатор (рис. 196). Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу, через конденсатор «протекают» токи смещения, причем в тех участках, где отсутствуют проводники.

Найдем количественную связь между изменяющимся электрическим и вызываемым им магнитным полями. По Максвеллу, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обклад­ками конденсатора существовал ток смещения, равный току в подводящих проводах. Тогда можно утверждать, что токи проводимости (I) и смещения (I _см) равны: I _см =I.

Ток проводимости вблизи обкладок конденсатора

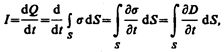(138.1)

(поверхностная плотность заряда s на обкладках равна электрическому смещению D в конденсаторе (см. (92.1)). Подынтегральное выражение в (138.1) можно рассматривать как частный случай скалярного произведения 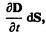когда 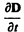и d S взаимно параллельны. Поэтому для общего случая можно записать

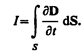
Сравнивая это выражение с 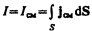(см. (96.2)), имеем

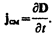(138.2)

Выражение (138.2) и было названо Максвеллом плотностью тока смещения.

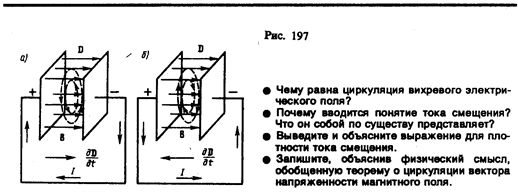
Рассмотрим, каково же направление векторов плотностей токов проводимости и смещения j и j _см. При зарядке конденсатора (рис. 197, а) через проводник, соединя­ющий обкладки, ток течет от правой обкладки к левой; поле в конденсаторе усиливается; следовательно, 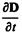>0, т. е. вектор 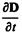направлен в ту же сторону, что и D. Из рисунка видно, что направления векторов 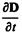и j совпадают. При разрядке конденсатора (рис. 197, б) через проводник, соединяющий обкладки, ток течет от левой обкладки к правой; поле в конденсаторе ослабляется; следовательно, 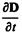<0, т. е. вектор 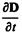направлен противоположно вектору D. Однако вектор 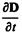направлен опять так же, как и вектор j. Из разобранных примеров следует, что направление вектора j, а следовательно, и вектора j _см, совпадает с направлением вектора 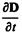, как это и следует из формулы (138.2).

Подчеркнем, что из всех физических свойств, присущих току проводимости, Макс­велл приписал току смещения лишь одно — способность создавать в окружающем пространстве магнитное поле. Таким образом, ток смещения (в вакууме или веществе) создает в окружающем пространстве магнитное поле (линии индукции магнитных полей токов смещения при зарядке и разрядке конденсатора показаны на рис. 197 штриховыми линиями).

В диэлектриках ток смещения состоит из двух слагаемых. Так как, согласно (89.2), D =e₀ E + P, где Е – напряженность электростатического поля, а Р — поляризованность (см. § 88), то плотность тока смещения

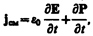(138.3)

где e₀ 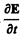— плотность тока смещения в вакууме, 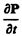— плотность тока поляризации — тока, обусловленного упорядоченным движением электрических зарядов в ди­электрике (смещение зарядов в неполярных молекулах или поворот диполей в поляр­ных молекулах). Возбуждение магнитного поля токами поляризации правомерно, так как токи поляризации по своей природе не отличаются от токов проводимости. Однако то, что и другая часть плотности тока смещения 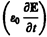, не связанная с движением зарядов, а обусловленная только изменением электрического поля во времени, также возбуждает магнитное поле, является принципиально новым утверждением Максвелла. Даже в вакууме всякое изменение во времени электрического поля приводит к возник­новению в окружающем пространстве магнитного поля.

Следует отметить, что название «ток смещения» является условным, а точ­нее — исторически сложившимся, так как ток смещения по своей сути — это изменя­ющееся со временем электрическое поле. Ток смещения поэтому существует не только в вакууме или диэлектриках, но и внутри проводников, по которым проходит переменный ток. Однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально А.А. Эйхенвальдом, изучавшим магнитное поле тока поляризации, который, как следует из (138.3), является частью тока смещения.

Максвелл ввел понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока

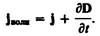
Введя понятия тока смещения и полного тока, Максвелл по-новому подошел к рас­смотрению замкнутости цепей переменного тока. Полный ток в них всегда замкнут, т. е. на концах проводника обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.

Максвелл обобщил теорему о циркуляции вектора Н (см. (133.10)), введя в ее правую часть полный ток I _полн = 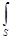j _полнd S сквозь поверхность S, натянутую на замкнутый контур L. Тогда обобщенная теорема о циркуляции вектора Н запишется в виде

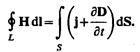(138.4)

Выражение (138.4) справедливо всегда, свидетельством чего является полное соответст­вие теории и опыта.

§ 139. Уравнения Максвелла для электромагнитного поля

Введение Максвеллом понятия тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зре­ния не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.

В основе теории Максвелла лежат рассмотренные выше четыре уравнения:

1. Электрическое поле (см. § 137) может быть как потенциальным (Е _Q), так и вихревым (Е _B), поэтому напряженность суммарного поля Е = Е _Q + Е _B. Так как цир­куляция вектора Е _Q равна нулю (см. (137.3)), а циркуляция вектора Е _B определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля

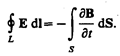
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):

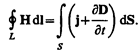
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущими­ся зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорема Гаусса для поля D (см. (89.3)):

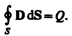(139.1)

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плот­ностью r, то формула (139.1) запишется в виде

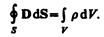
4. Теорема Гаусса для поля В (см. (120.3)):

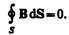
Итак, полная система уравнений Максвелла в интегральной форме:

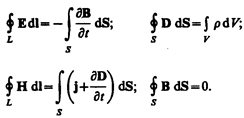
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):

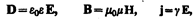
где e ₀ и m ₀ — соответственно электрическая и магнитная постоянные, e и m — соответст­венно диэлектрическая и магнитная проницаемости, g — удельная проводимость веще­ства.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Мак­свелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.

Для стационарных полей (E= const и B= const ) уравнения Максвелла примут вид

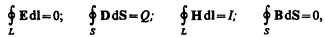
т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.

Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса

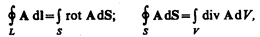
можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):

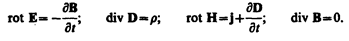
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная — эквивалентны. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.

Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму допол­няют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше (см. § 90, 134):

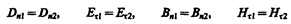
(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).

Уравнения Максвелла — наиболее общие уравнения для электрических и магнит­ных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что перемен­ное магнитное поле всегда связано с порождаемым им электрическим полем, а пере­менное электрическое поле всегда связано с порождаемым им магнитным, т. е. элект­рическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.

Теория Максвелла, являясь обобщением основных законов электрических и магнит­ных явлений, не только смогла объяснить уже известные экспериментальные факты, что также является важным ее следствием, но и предсказала новые явления. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения (см. § 138), что позволило Максвеллу предсказать существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. В дальнейшем было доказано, что скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме равна скорости света с = 3×10⁸ м/с. Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны. Электромагнитные волны на опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что законы их возбуждения и распространения полностью описываются уравнениями Максвелла. Таким образом, теория Максвелла была экс­периментально подтверждена.

К электромагнитному полю применим только принцип относительности Эйн­штейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью с не совместим с принципом относи­тельности Галилея.

Согласно принципу относительности Эйнштейна, механические, оптические и элект­ромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т. е. описываются одинаковыми уравнениями. Уравнения Максвелла инвариантны относительно преобразований Лоренца: их вид не меняется при переходе от одной инерциальной системы отсчета к другой, хотя величины Е, В, D, Н в них преобразуются по определенным правилам.

Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Taк, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный относительно одной инерциальной системы отсчета про­водник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле.

Таким образом, теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, маг­нитных и оптических явлений, базирующейся на представлении об электромагнитном поле.

4 КОЛЕБАНИЯ И ВОЛНЫ

Глава 18 Механические и электромагнитные колебания

§ 140. Гармонические колебания и их характеристики

Колебаниями называются движения или процессы, которые характеризуются опреде­ленной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качание маятника часов, переменный электрический ток и т. д. При колебательном движении маятника изменяется координата его центра масс, в случае переменного тока колеблются напряжение и ток в цепи. Физическая природа колебаний может быть разной, поэтому различают колебания механические, электро­магнитные и др. Однако различные колебательные процессы описываются одинаковы­ми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природы. Например, единый подход к изучению механических и электромагнитных колебаний применялся английским физиком Д. У. Рэлеем (1842—1919), А. Г. Столетовым, русским инжене­ром-экспериментатором П. Н. Лебедевым (1866—1912). Большой вклад в развитие теории колебаний внесли Л. И. Мандельштам (1879—1944) и его ученики.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воз­действий на колебательную систему (систему, совершающую колебания). Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеб­лющаяся величина изменяется со временем по закону синуса (косинуса). Рассмотрение гармонических колебаний важно по двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; 2) различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний. Гармонические колеба­ния величины s описываются уравнением типа