Пусть функция z=f (x,y)определена и непрерывна в ограниченной замкнутой области D плоскости Oxy. Разобьем область D произвольным образом на n областей S 1, S 2, …, Sn, которые назовем элементарными областями. В каждой из элементарных областей произвольным образом выберем по точке: 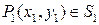 ,
, 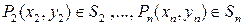 , которые назовем точками пунктуации. Обозначим через
, которые назовем точками пунктуации. Обозначим через 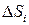 - площадь, через
- площадь, через 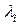 - диаметр i- ойэлементарной области (i= 1,…, n),
- диаметр i- ойэлементарной области (i= 1,…, n), 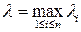 . Составим выражение
. Составим выражение
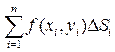 (1)
(1)
Выражение (1) называется интегральной суммой Римана для функции z=f (x,y)по области D. Заметим, что она зависит от способа разбиения области D на элементарные области и от способа выбора точек пунктуации.
Если существует предел интегральной суммы Римана (1) при 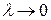 , и этот предел не зависит ни от способа разбиения области на элементарные области, ни от выбора точек пунктуации, то он называется двойным интегралом от функции z=f (x,y)по области D и обозначается
, и этот предел не зависит ни от способа разбиения области на элементарные области, ни от выбора точек пунктуации, то он называется двойным интегралом от функции z=f (x,y)по области D и обозначается
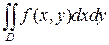
Таким образом,
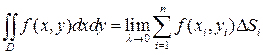 (2)
(2)
Свойства двойных интегралов аналогичны свойствам определенных интегралов. Отметим два, наиболее часто используемых на практике, свойства.
|
|
|
1) Свойство линейности. Если функции f (x,y)и g(x,y) интегрируемы по области D, то справедлива формула:
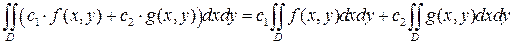
2) Свойство аддитивности. Если область D разбита на две области D 1 и D 2 без общих точек, и функция f (x,y)интегрируема во всех точках области D, то справедлива формула:
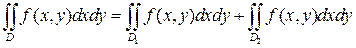
Вычисление двойных интегралов сводится к вычислению повторных интегралов следующим образом. Пусть область D ограничена слева и справа вертикальными прямыми x=a, x=b, а снизу и сверху – кривыми 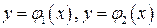 ,причем
,причем 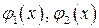 - непрерывны и
- непрерывны и 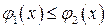 на промежутке [ a,b ](Рис.1).Такую область назовем правильной в направлении оси Oy. Тогда
на промежутке [ a,b ](Рис.1).Такую область назовем правильной в направлении оси Oy. Тогда
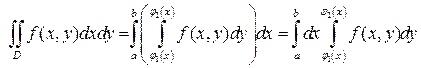 , (3)
, (3)
причем сначала вычисляется интеграл по переменной y (x - параметр), а полученный результат интегрируется по x.
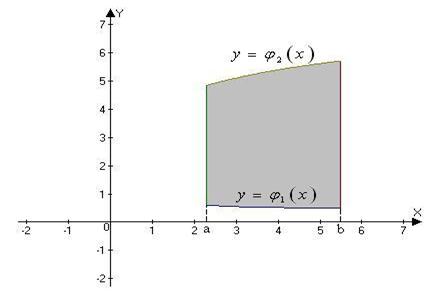
Рис.1.
Заметим, что если кривая 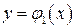 (или
(или 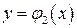 ) на промежутке [ a,b ]задается различными аналитическими выражениями, например,
) на промежутке [ a,b ]задается различными аналитическими выражениями, например,
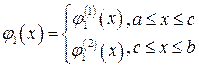 ,
,
то интеграл справа в (3) записывается в виде суммы двух интегралов:
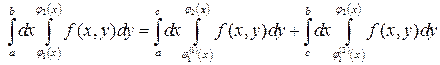 .
.
Аналогично, пусть область D ограничена снизу и сверху горизонтальными прямыми y=c, y=d, а слева и справа - кривыми 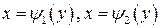 , причем
, причем 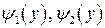 непрерывны и
непрерывны и 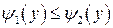 на промежутке [ c,d ](Рис.2). Такую область назовем правильной в направлении оси Ox. Тогда
на промежутке [ c,d ](Рис.2). Такую область назовем правильной в направлении оси Ox. Тогда
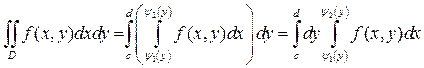 (4)
(4)
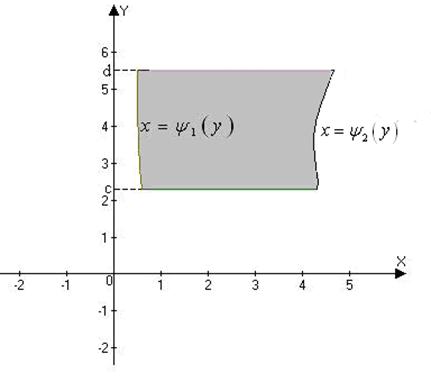
Рис. 2
Теорема (о замене переменных в двойном интеграле)
Пусть выполняются условия:
1) функции x=x (u, v) и y=y (u, v)таковы, что каждой точке с координатами (x, y) из области D соответствует единственная точка с координатами (u, v) из области D 1 и наоборот;
2) функции x=x (u, v) и y=y (u, v)имеют непрерывные частные производные по переменным u и v в области D 1;
3) функция z=f (x, y) определена и интегрируема в области D.
Тогда справедлива формула:
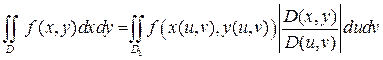 , (5)
, (5)
где
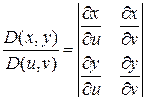
- якобиан перехода от декартовых координат к криволинейным координатам.
|
|
|
Частным случаем криволинейных координат для двойного интеграла являются полярные координаты:
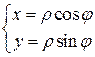 ,
,
для которых якобиан равен 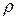 и формула (5) примет вид:
и формула (5) примет вид:
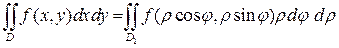 (6)
(6)
Задание 1. Вычислить повторный интеграл: 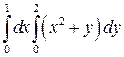 .
.
Решение. Вычислим сначала интеграл по переменной y (x - параметр). Имеем
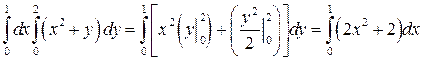 .
.
Полученный интеграл является обычным определенным интегралом. Окончательно имеем
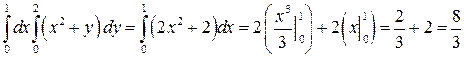 .
.
Задание 2. Записать данный двойной интеграл в виде повторных, взятых в различных порядках:
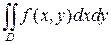 ,
,
область интегрирования D ограничена линиями x= 2, y=x, y= 1 /x.
Решение. Построим область интегрирования D (рис.3).
1)По формуле (3) при a= 1, b= 2, 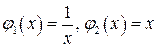 получаем
получаем
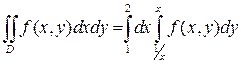 .
.
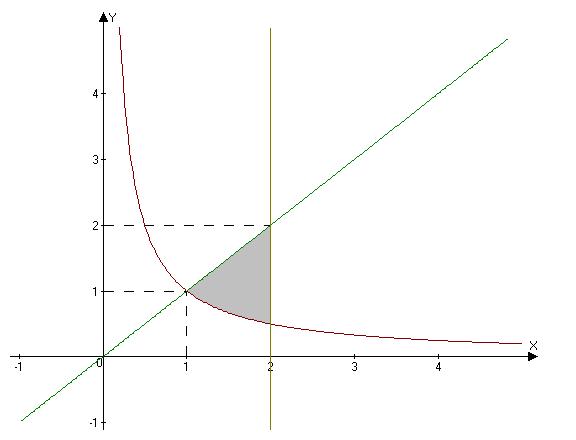
Рис. 3.
2) Если же для вычисления данного интеграла применить формулу (4), то надо положить c= 1/2, d= 2, 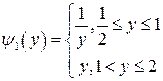 ,
, 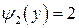 .
.
 Тогда
Тогда
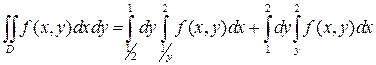 .
.
Задание 3. Изменить порядок интегрирования в повторном интеграле:
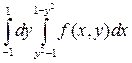 .
.
Решение. Область интегрирования D ограничена снизу кривой
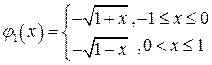 ,
,
сверху кривой
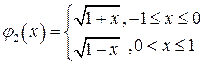
и представлена на рис. 4.
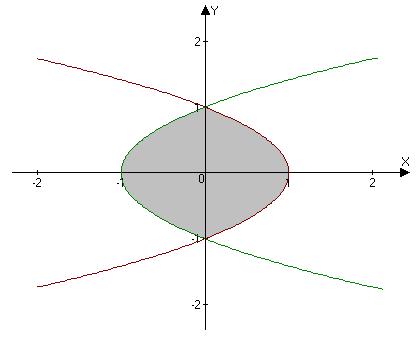
Рис. 4.
Поэтому имеем
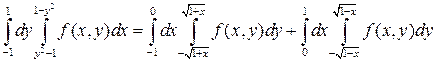 .
.
Задание 4. Перейдя к полярным координатам, вычислить интеграл:
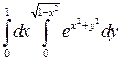 .
.
Решение. Положим
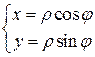
и применим формулу (6). Так как 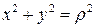 , то
, то
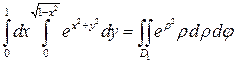 .
.
Областью интегрирования исходного интеграла является четверть круга радиуса R=1 с центром в начале координат (рис. 5).
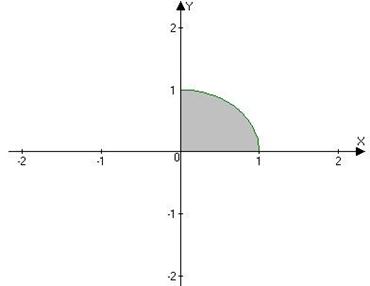
Рис. 5.
Следовательно, в области D 1 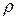 изменяется от 0 до 1 и
изменяется от 0 до 1 и 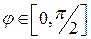 . Таким образом, имеем:
. Таким образом, имеем:
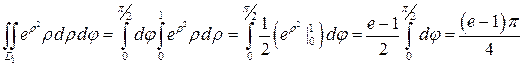 .
.
 2015-01-21
2015-01-21 4837
4837
