Зададимся целью придать интерполяционной формуле более простой вид, подобный широко используемой в математическом анализе формулы Тейлора.
Такая структура интерполяционного многочлена позволила бы более просто перестраивать его степень, добавляя или отбрасывая удаленные от начала его записи члены.
Будем считать, что интерполируемая функция y=f(x) задана своими значениями y0, y1,…, yn на системе равноотстоящих узлов
x0, x1, …, xn, т.е. таких, что любой узел этой сетки можно представит в виде
xi=x0+ih,
где i=0, 1,…,n, а h>0 - некоторая постоянная величина, называемая шагом сетки.
Прежде чем строить желаемые интерполяционные формулы, рассмотрим элементы конечных разностей.
Конечная разность 1- го порядка есть разность между значениями функции:
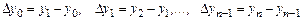
Конечная разность 2 – го порядка
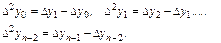
Этот процесс построения разностей может быть продолжен, и описывается рекуррентной формулой, выражающей конечную разность
k - го порядка 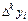 через разности (k-1) порядка:
через разности (k-1) порядка:
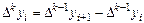
k=1, 2,…,, n 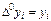
Конечные разности разных порядков удобно помещать в одну общую таблицу с узлами и значениями функции (последние можно интерпретировать как конечные разности нулевого порядка). Эту общую таблицу называют таблицей конечных разностей.
| x0 | y0 | Dy0 | D2y0 | D3y0 | D4y0 | . |
| x1 | y1 | Dy1 | D2y1 | D3y1 | D4y1 | . |
| x2 | y2 | Dy2 | D2y2 | D3y2 | ||
| x3 | y3 | Dy3 | D2y3 | |||
| x4 | y4 | Dy4 | ||||
| x5 | y5 | |||||
| . | . |
Будем строить интерполяционный многочлен Pn(x) в форме:
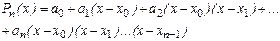 (2)
(2)
Его n+1 коэффициент 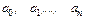 будем находить последовательно из n+1 интерполяционных равенств
будем находить последовательно из n+1 интерполяционных равенств
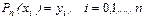 ,а именно, полагая i=0, т.е.
,а именно, полагая i=0, т.е. 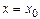
Имеем 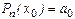 , а по условию интерполяции
, а по условию интерполяции 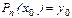 , следовательно,
, следовательно, 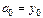
Далее, при i=1, аналогично получаем равенство
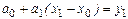 ,
,
в которое подставляем уже найденное значение 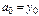 .
.
Разрешая это равенство относительно, 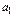 и используя обозначение конечной разности, получаем
и используя обозначение конечной разности, получаем
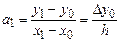
Следующий шаг, при i=2, дает
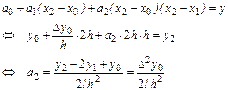
Полной индукцией можно доказать справедливость выражения
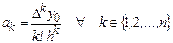 (3)
(3)
Подставляя найденные коэффициенты 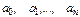 в (2), получаем многочлен
в (2), получаем многочлен
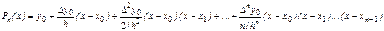
(4)
который называют первым интерполяционным многочленом Ньютона..
Учитывая, что каждое слагаемое многочлена, начиная со второго, содержит множитель 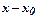 , естественно предположить, что этот многочлен наиболее приспособлен для интерполирования в окрестности узла
, естественно предположить, что этот многочлен наиболее приспособлен для интерполирования в окрестности узла 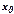
(при 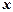 , близких к
, близких к 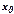 ,
, 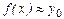 ).
).
Будем называть узел 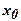 базовым для многочлена (4), и упростим (4) введением новой переменной
базовым для многочлена (4), и упростим (4) введением новой переменной 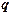 равенством
равенством 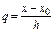 , или (что - то же) равенством
, или (что - то же) равенством 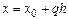 .
.
Так как при любых
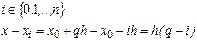
то в результате подстановки этих разностей в (4) приходим к первой интерполяционной формуле Ньютона в виде
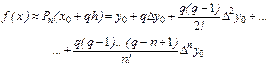 (5)
(5)
где обозначение 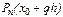 указывает не только на n – ю степень многочлена, но и на базовый узел
указывает не только на n – ю степень многочлена, но и на базовый узел 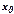 и связь переменных
и связь переменных 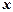 и
и 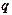 .
.
Первая формула Ньютона обычно применяется при значениях 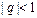 , а именно, для интерполирования вперед, (при
, а именно, для интерполирования вперед, (при 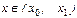 ,
,
т. е. при 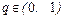 ) и экстраполирования назад (при
) и экстраполирования назад (при 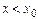 ,
,
т.е. при 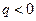 ).
).
Для интерполирования в конце таблицы форма интерполяционного многочлена 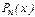 берется такой, которая предусматривает поочередное подключение узлов в обратном порядке: сначала последний, потом предпоследний и т. д., т. е.
берется такой, которая предусматривает поочередное подключение узлов в обратном порядке: сначала последний, потом предпоследний и т. д., т. е.
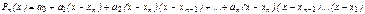 (6)
(6)
Коэффициенты 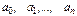 этого многочлена находятся аналогично тому, как они находились для многочлена (2), только здесь подстановка узловых точек вместо
этого многочлена находятся аналогично тому, как они находились для многочлена (2), только здесь подстановка узловых точек вместо 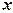 и рассмотрение интерполяционных равенств производится тоже в обратном порядке.
и рассмотрение интерполяционных равенств производится тоже в обратном порядке.
Полагая 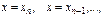 , имеем:
, имеем:
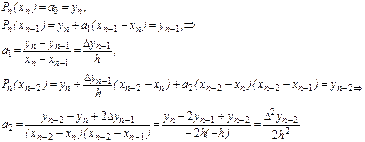
и т. д. В общем случае 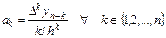
Таким образом, получаем второй интерполяционный многочлен Ньютона
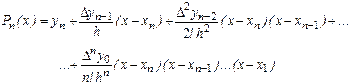 (7)
(7)
В котором базовым является узел 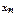 и коэффициенты которого определяются конечными разностями, расположенными на восходящей диагонали от
и коэффициенты которого определяются конечными разностями, расположенными на восходящей диагонали от 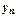 .
.
Положим в (7) 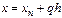 , иначе, введем новую переменную
, иначе, введем новую переменную 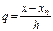 и преобразуем к ней входящие в (7) разности:
и преобразуем к ней входящие в (7) разности:
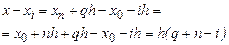
В результате приходим ко второй интерполяционной формуле Ньютона вида
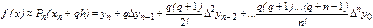
(8)
Ее также целесообразно использовать при значениях 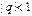 , т.е. в окрестности узла
, т.е. в окрестности узла 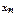 для интерполирования назад (при
для интерполирования назад (при 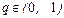 ) и эктраполирования вперед (при
) и эктраполирования вперед (при 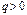 ).
).
Наряду с выведенными специально для начала и конца таблицы первой и второй интерполяционными формулами Ньютона, имеется еще несколько формул, рассчитанных на их применение в центральной части таблицы (интерполяционная формула Стирлинга и формула Бесселя).
Теперь о том, как могут быть трансформированы остаточный член и его оценки при конечно – разностной интерполяции.
В силу доказанной единственности интерполяционного многочлена Лагранжа, все построенные здесь интерполяционные многочлены Ньютона – это всего лишь различные формы его представления. Следовательно, для всех этих форм справедливо выражение остаточного члена, полученного для многочлена Лагранжа.
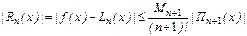
где 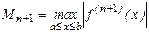
Для случая равноотстоящих узлов 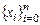 многочлен
многочлен 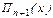 преобразуется к новой переменной
преобразуется к новой переменной 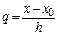 следующим образом:
следующим образом:
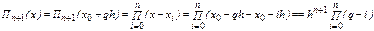
Отсюда
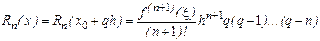
Итак, для 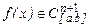 ,. конечно - разностная интерполяционная формула Ньютона степениn с базовым узлом
,. конечно - разностная интерполяционная формула Ньютона степениn с базовым узлом 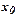 может быть записана в виде
может быть записана в виде
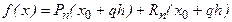 , в котором
, в котором 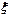 - некоторая неизвестная, но фиксированная (при фиксированном
- некоторая неизвестная, но фиксированная (при фиксированном 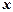 ) точка интервала
) точка интервала 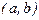 .
.
Аналогично, при выборе базового узла 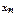 , т. е. для второй интерполяционной формулы Ньютона, получаем точное представление
, т. е. для второй интерполяционной формулы Ньютона, получаем точное представление
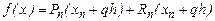 , где
, где
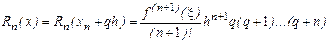
В силу связи (формула (1)) между производными и конечными разностями, выражение для (n+1) – ой производной
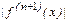
приближенно можно заменить на величину
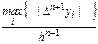 .
.
В этом случае степень n интерполяционного многочлена должна быть заниженной по сравнению с n числом узлов (иначе конечная разность 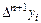 (n+1) – го порядка равна нулю).
(n+1) – го порядка равна нулю).
 2015-02-24
2015-02-24 473
473








