Изоморфные автоматы

Как указывалось в § 2.2, обозначение состояний не имеет какого-либо особого значения и может выбираться произвольно. Автоматы, у которых характеристические функции одинаковы, за исключением возможных различий в обозначениях состояний, называются изоморфными друг другу. Если задан автомат М, представляющий определенную систему, то любой автомат, изоморфный к М, также может служить представлением этой системы. Следовательно, представление системы автоматом ни в коем случае не единственно.

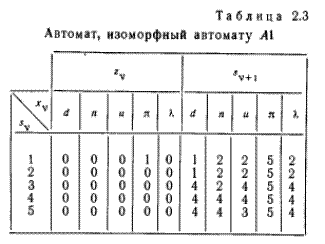
Пусть М является (n, р, q) - автоматом, определенным таблицей переходов, такой, как таблица 2.1. Рассмотрим другую таблицу переходов, полученную из таблицы переходов автомата М путем перестановки символов σ₁, σ₂,..., σ_n с последующей записью строк в том порядке, в котором они были выписаны в исходной таблице. В результате получится таблица, представляющая автомат, изоморфный автомату М. Множество всех различных автоматов, получающихся в результате всех возможных n! таких перестановок, называется семейством перестановок автомата М. Ясно, что не обязательно две различные перестановки приводят к получению двух различных таблиц переходов и, следовательно, мощность семейства перестановок может быть меньше, чем n!. Следует также заметить, что два автомата, принадлежащие различным семействам перестановок, не могут быть изоморфными друг другу. В качестве примера таблицей 2.3 представлен автомат, изоморфный автомату А1, представленному таблицей 2.2. Он получен заменой первоначальных обозначений состояний 1, 2, 3, 4 и 5 на 5, 4, 3, 2 и 1 соответственно.

Лемма 2.1. Мощность семейства перестановок явно минимального (n, р, q) -автомата равна n1.

Доказательство. Строки в таблице z_v явно минимального автомата различны по определению и остаются различными после перестановки обозначений состояний. Поэтому таблицы, получаемые в результате различных перестановок, различны. Так как число различных перестановок равно n!, то лемма доказана.

Теорема 2.1. Мощность N^(ЯМ)n,p,q класса явно минимальных (n, р, q) - автоматов, не содержащего изоморфных автоматов, определяется формулой

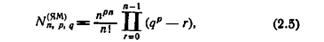
где отрицательные значения N^(ЯМ)n,p,q принимаются равными нулю.

Доказательство. Множество явно минимальных (n, р, q) - автоматов является объединением[8] семейств перестановок всех автоматов класса, определенного в теореме. Поскольку эти семейства перестановок являются непересекающимися[9] и по лемме 2.1 каждое семейство содержит точно n1 различных автоматов, имеем:

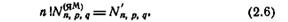
где N'n,p,q — мощность класса явно минимальных (n, р, q) - автоматов, определяемая уравнением (2.2). Теорему доказывает решение (2.6) относительно N^(ЯМ)n,p,q.