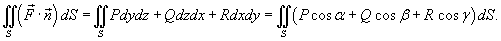
Потоком векторного поля 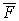 через поверхность
через поверхность 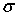 называется поверхностный интеграл
называется поверхностный интеграл
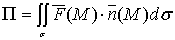 , где
, где 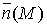 – единичный вектор нормали в произвольной точке
– единичный вектор нормали в произвольной точке 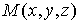 .
.
16. Пусть в 3-х мерном пространстве задана некоторая область V. Предположим что каждой точке в области V поставлена в соответствии некоторое число, тогда говорят, что в области V определено скалярное поле. (Задание скалярного поля эквивалентно заданию функции, определенной областью V)
Пусть в некоторой области V поставим в соответствии некий вектор, тогда говорят что в области V задано векторное поле.
Определение 3: Градиентом дифференцируемого скалярного поля u(M)=u(x,y,z) называется вектор
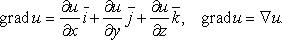
Определение 4: Дивергенцией (или расходимостью) дифференцируемого векторного поля 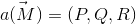 называется скаляр
называется скаляр
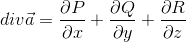
Определение 5: Ротором (или вихрем) дифференцируемого векторного поля 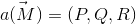 называется вектор
называется вектор
который с помощью символической записи удобно представить в виде векторного произведения
Циркуля́цией ве́кторного по́ля по данному замкнутому контуру Γ называется криволинейный интеграл второго рода, взятый по Γ. По определению
|
|
|
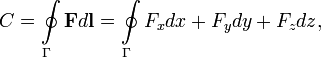
где 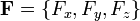 — векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ,
— векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ, 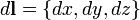
16,. Формула Остроградского-Гаусса связывает поверхностные интегралы второго рода с соответствующими тройными интегралами.
Данную формулу можно записать также в координатной форме:
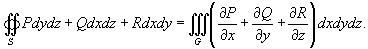
Теорема Стокса связывает между собой криволинейные интегралы второго рода и поверхностные интегралы второго рода.
В координатной форме теорема Стокса может быть записана в следующем виде:
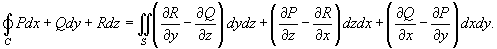
Формула Стокса в символической форме
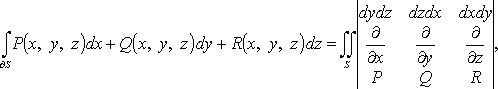
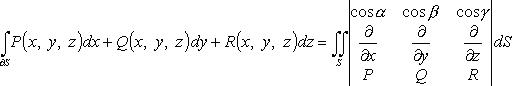
(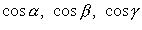 - направляющие косинусы нормали, соответствующей выбранной стороне поверхности.
- направляющие косинусы нормали, соответствующей выбранной стороне поверхности.
формула Грина
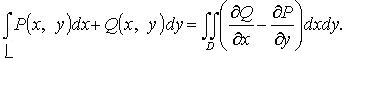
13.
14.
15.
16.
17.
18.
19.
20.
21. Интегральный признак Коши. Примеры.
| Интегральный признак Коши |
Пусть f (x) является непрерывной, положительной и монотонно убывающей функцией на промежутке [1, +∞). Тогда ряд
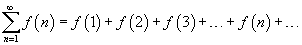 сходится, если сходится несобственный интеграл
сходится, если сходится несобственный интеграл 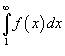 , и расходится, если , и расходится, если 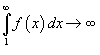 . .
|
| Пример 1 |
Определить, сходится или расходится ряд 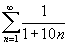 .
Решение.
Используем интегральный признак Коши. Вычислим соответствующий несобственный интеграл: .
Решение.
Используем интегральный признак Коши. Вычислим соответствующий несобственный интеграл:
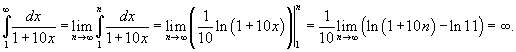 Таким образом, данный ряд расходится.
Таким образом, данный ряд расходится.
|
| Пример 2 |
Показать, что обобщенный гармонический ряд 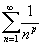 сходится при p > 1.
Решение.
Рассмотрим соответствующую функцию сходится при p > 1.
Решение.
Рассмотрим соответствующую функцию 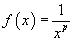 и применим интегральный признак. Несобственный интеграл равен и применим интегральный признак. Несобственный интеграл равен
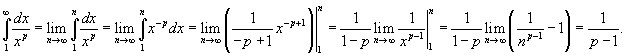 Видно, что обобщенный гармонический ряд сходится при значении p > 1.
Видно, что обобщенный гармонический ряд сходится при значении p > 1.
|
| Пример 3 |
Определить, сходится или расходится ряд 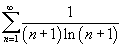 .
Решение.
Вычислим соответствующий несобственный интеграл: .
Решение.
Вычислим соответствующий несобственный интеграл:
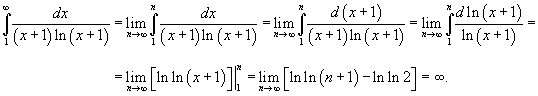 Таким образом, данный ряд расходится.
Таким образом, данный ряд расходится.
|
| Пример 4 |
Исследовать ряд 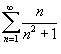 на сходимость.
Решение.
Оценим несобственный интеграл на сходимость.
Решение.
Оценим несобственный интеграл
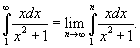 Сделаем замену:
Сделаем замену: 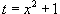 . Тогда . Тогда 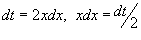 . Находим значение интеграла: . Находим значение интеграла:
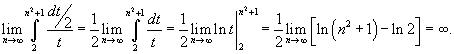 Поскольку данный интеграл расходится, то ряд
Поскольку данный интеграл расходится, то ряд 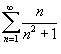 также расходится. также расходится.
|
| Пример 5 |
Исследовать ряд 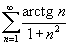 на сходимость.
Решение.
Заметим, что на сходимость.
Решение.
Заметим, что 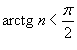 . Тогда по признаку сравнения получаем . Тогда по признаку сравнения получаем
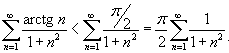 Используя интегральный признак, оценим сходимость ряда
Используя интегральный признак, оценим сходимость ряда 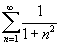 : :
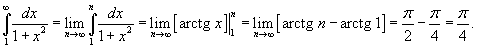 Поскольку несобственный интеграл сходится, то исходный числовой ряд также сходится.
Поскольку несобственный интеграл сходится, то исходный числовой ряд также сходится.
|
| Пример 6 |
Определить, сходится или расходится ряд 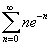 .
Решение.
Применяя интегральный признак, вычислим соответствующий несобственный интеграл: .
Решение.
Применяя интегральный признак, вычислим соответствующий несобственный интеграл:
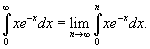 Интегрируем по частям:
Интегрируем по частям:
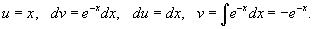 Получаем
Получаем
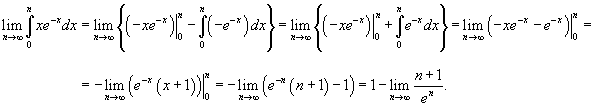 Предел в последнем выражении можно оценить по правилу Лопиталя:
Предел в последнем выражении можно оценить по правилу Лопиталя:
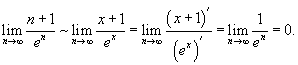 Следовательно, несобственный интеграл конечен и равен 1. Поэтому, исходный ряд сходится.
Следовательно, несобственный интеграл конечен и равен 1. Поэтому, исходный ряд сходится.
|
22. Знакопеременные ряды. Теорема Лейбница о сходимости знакочередующегося ряда и оценка остатка.
|
|
|
| Знакопеременные ряды. Абсолютная и условная сходимость |
Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.
Признак Лейбница
Для знакочередующихся рядом действует достаточный признак сходимости Лейбница. Пусть { an } является числовой последовательностью, такой, что
1. an +1 < an для всех n; 2. 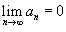 .
Тогда знакочередующиеся ряды .
Тогда знакочередующиеся ряды 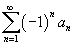 и и 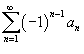 сходятся.
Оценка остатка знакочередующегося ряда Пусть знакочередующийся числовой ряд сходится по признаку Лейбница и его сумма равна S. Обозначим через Sn частичную сумму ряда, включающую n членов. Тогда остаток знакочередующегося ряда по абсолютной величине меньше модуля первого отброшенного слагаемого: | S − Sn | < | an +1|. сходятся.
Оценка остатка знакочередующегося ряда Пусть знакочередующийся числовой ряд сходится по признаку Лейбница и его сумма равна S. Обозначим через Sn частичную сумму ряда, включающую n членов. Тогда остаток знакочередующегося ряда по абсолютной величине меньше модуля первого отброшенного слагаемого: | S − Sn | < | an +1|.
|
 2015-02-04
2015-02-04 1488
1488








