Другие непрерывные распределения

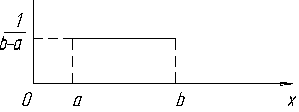
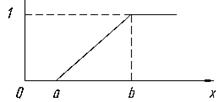
Равномерное распределение - наиболее простое, имеющее область значений a ≤ x ≤ b (рис. 5.4). Интегральную функцию равномерного распределения можно представить в аналитическом виде (5.8).

а б

Рис. 5.4. Функция плотности f(x) (а) и интегральная функция F(x) (б) равномерного распределения

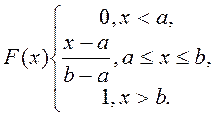(5.8)

Ниже приводятся основные числовые характеристики равномерного распределения:

- математическое ожидание (среднее)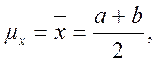

- дисперсия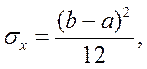

- эксцесс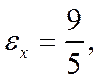

- асимметрия .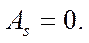

Широко применяются в прикладной статистике некоторые распределения, тесно связанные с нормальным.

t – распределение Стьюдента (СТЬЮДРАСП) определяет распределение выборок, произведённых из распределённой по нормальному закону генеральной совокупности, и зависит от объёма выборки n (рис. 5.5). Поскольку, как правило, на практике используются именно выборки, t–распределение и его производные имеют огромное значение при анализах самих выборок и результатов выполненных на их базе расчётов.

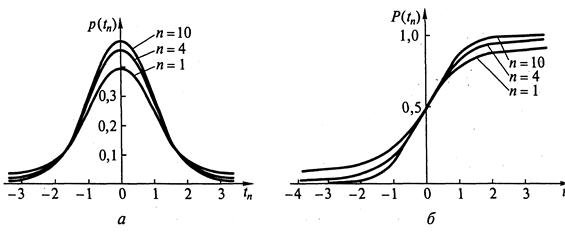
Рис. 5.5. Плотность f (а) и интегральная функция F (б) распределения Стьюдента

С увеличением объёма выборки n распределение Стьюдента (см. рис. 5.5) стремится к нормальному распределению, соответственно значения f и F приближаются к наблюдаемым при нормальном распределении (см. рис. 5.1). Принято считать, что при n > 30 без существенных погрешностей можно заменять t – распределение нормальным распределением. Но при малых выборках для оценки ошибки, возникающей при определении математического ожидания, используют t – критерий Стьюдента:

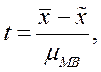(5.9)

где 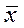- генеральная средняя; 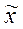- выборочная средняя; 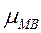- мера случайных колебаний выборочной средней в малой выборке, зависящая от её объёма:

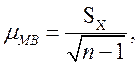где 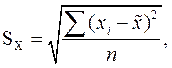(5.10)

t – распределение используется для решения множества задач математической статистики, в частности при анализе малых выборок, в теории ошибок, методе наименьших квадратов. В частности, поскольку все ошибки в определении среднего связаны с ошибкой среднего значения выборки относительно среднего значения генеральной совокупности, на t- распределении основаны критерии проверки гипотез о равенстве средних (§ 7.4.3), значимости коэффициентов регрессии и т.д. [28, 29].

Распределение c 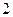«хи-квадрат» ( распределение Пирсона).

Если имеется несколько нормально распределенных случайных величин: Х₁, Х₂,…, Х_n, то сумма их квадратов является случайной величиной, распределенной по закону «хи-квадрат».

Отсюда следует, что дисперсия случайной величины, (определяется как сумма квадратов (3.3), см. § 3.2), распределенной по нормальному закону, в свою очередь распределена по закону «хи-квадрат».

Распределение Пирсона используется для сравнения предполагаемых (теоретических) и наблюдаемых значений в некотором распределении, см. § 7.6. Сравнивая наблюдаемые результаты с предполагаемыми, можно определить, была ли обоснованной исходная гипотеза о распределении некоторой случайной величины.

Плотность распределения Пирсонавыражаются формулой (5.11), а «критерий согласия» c² - формулой (5.12).

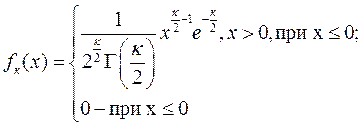(5.11)

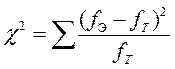(5.12)

где Г - гамма-функция (интеграл Эйлера второго рода) [30]. Она обладает рядом интересных свойств; в частности, Г(п + 1) = п!. График плотности этого распределения представлен на рис. 5.6. Из рис. 5.6 и из выражения (5.11) можно сделать заключение, что распределение «хи-квадрат» определяется одним параметром – "числом степеней свободы" k = n - 1 (обозначается также f или df), а также что с увеличением k распределение «хи-квадрат» приближается к нормальному распределению. Действительно, видно, что с увеличением n (см. n = 10, то есть k = 9) график становится всё более симметричным, приобретая форму, характерную для графика плотности нормального распределения (см. рис. 5.1).

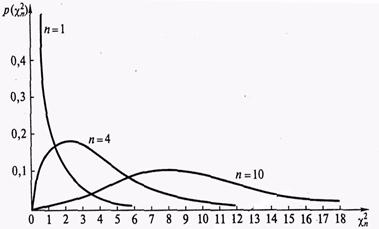
Рис. 5.6. Плотность распределения Пирсона

F – распределение Фишера (FРАСП), называемое также «дисперсионным отношением» Фишера-Снедекора, используется в разделах статистики, занимающихся проверкой гипотез (см. главу 7) равенства двух выборочных дисперсий, например в дисперсионном и регрессионном анализах. Необходимость этой операции, как и в предыдущем случае, обусловлена заменой генеральных совокупностей выборками и связанными с этим погрешностями. Действительно, равенство дисперсий генеральных совокупностей не нуждается в проверке.

Если две независимые случайные величины со степенями свободы k₁ и k₂ имеют распределение хи-квадрат (именно таким образом распределены дисперсии, см. выше), то их отношение является распределением Фишера - Снедекора.

На рис. 5.7 представлен график плотности этого распределения для случая, когда объём одной выборки n₁ = 20, а объём второй выборки (n₂) различается от n₂ =10 до n₂ = ∞.

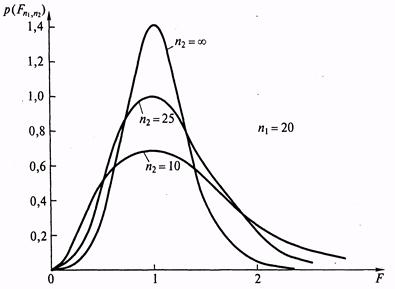
Рис. 5.7. Частные случаи плотности F – распределения Фишера.

Интегральная функция этого распределения для выборок со степенями свободы k и l имеет вид:

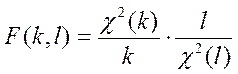(5.13)

Гамма-распределение (ГАММАРАСП) можно использовать для изучения случайных величин, которые имеют асимметричное распределение. Гамма-распределение обычно используется в теории очередей, например при анализе количества деталей, скопившихся на какой-то стадии производства.

Плотность гамма - распределения определяется выражением (5.14) для условий 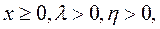а 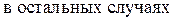- 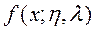= 0. Интегральная функция определяется выражением (5.15).

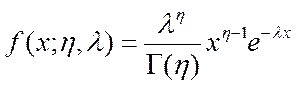(5.14)

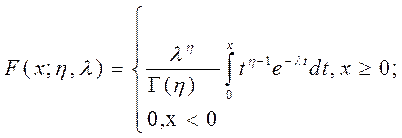(5.15)

Бета-распределение (БЕТАРАСП) обычно используется для изучения вариации в процентах какой-либо величины, например доли смены, которую работник занят непосредственно на выполнение операции. Плотность и интегральная функция этого распределениявыражаются соответственно формулами (5.16) и (5.17)

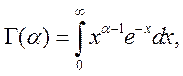(5.16)

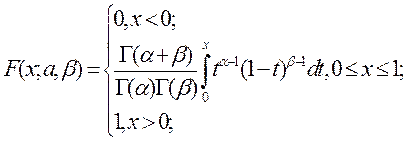(5.17)

Логарифмическое нормальное распределение (ЛОГНОРМРАСП) используется для анализа данных, которые предварительно были логарифмически преобразованы. Плотность и интегральная функция логарифмического нормального распределениявыражаются формулами (5.18) и (5.19)

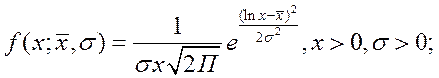(5.18)

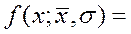
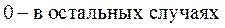
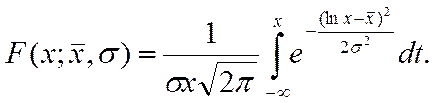(5.19)

Экспоненциальное распределение (ЭКСПРАСП), представленное формулами (5.20) и (5.21) используется для моделирования временных задержек между событиями. Функцию ЭКСПРАСП можно, в частности, использовать, чтобы определить вероятность того, что этот процесс займет не более k минут.

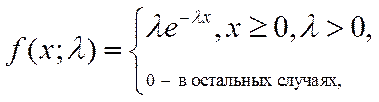(5.20)

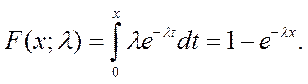(5.21)

Распределение Вейбулла (ВЕЙБУЛЛ) обычно используется при анализе надежности, например, для вычисления среднего времени наработки до отказа какого-либо устройства. Плотность и интегральная функция распределенияВейбулла выражаются формулами (5.22) и (5.23).

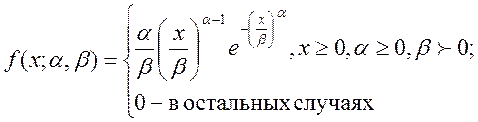(5.22)

(5.23)

5.3 Основные дискретные распределения,

Следует выделить 3 дискретные распределения, используемые для контроля и управления качеством производственных процессов: биномиальной (Бернулли), гипергеометрическое и распределение Пуассона.

Биномиальное распределение. Во многих инженерных задачах рассматри­ваются независимые многократно повторяемые испытания, на­зываемые испытаниями Бернулли. Каждое такое испытание при­водит к одному из двух возможных исходов, называемых часто «ус­пехом» и «неудачей», и вероятность успеха р не меняется от одного опыта к другому. В производстве вероятность успеха р может выражать вероятность получения годной детали, которая определяется, например, путём расчёта интегральной функции нормального распределения, см., например, § 5.4.1. Часто бывает необходимо знать вероятность появления ровно х (или не менее х) успешных исходов при n неза­висимых испытаниях. Например, известно, что вероятность получения одной годной детали (каждой детали из партии) р = 0,95. По условиям контракта партия принимается заказчиком, если при испытании выборки из 10 деталей все окажутся годными. Требуется определить вероятность благополучной приёмки этих деталей.

Согласно закону умножения независимых событий вероят­ность появления определенной последовательности х успешных и n-х неудачных исходов в n испытаниях равна р^x(1-р)^n-x, где р- вероятность успеха при одном испытании. Из комбинаторики известно, что при n испытаниях х успешных и n-х неудачных ис­ходов могут появиться С^x_n различными одинаково возможными способами:

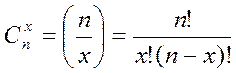(5.24)

Согласно закону сложения взаимно исключа­ющих событий вероятность появления ровно х успешных исходов в n независимых испытаниях определяется распределением, полу­чившим название биномиального (или распределения Бернулли):

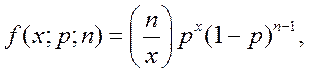(5.25)

где p - вероятность успеха при одном испытании.

Вероятность появления не более r успешных исходов в n неза­висимых испытаниях задается интегральной функцией биноми­ального распределения (5.26):

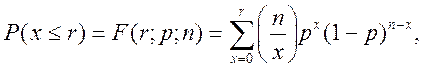(5.26)

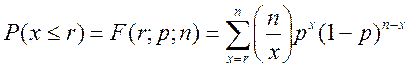
а вероятность появления не менее r успешных исходов в n незави­симых испытаниях - интегральной функцией (5.27):

(5.27)

Математическое ожидание 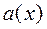и дисперсия 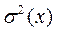биномиального рас­пределения представлены выражениями (5.28) и (5.29):

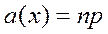(5.28)

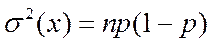(5.29)

Биномиальное распределение симметрично при р = 0,5. При р ≠ 0,5 распределение приближается к симметричному при уве­личении n; приближение будет происходить тем быстрее, чем ближе значение р к 0,5, Кроме того, при увеличении n биноми­альное распределение можно аппроксимировать нормальным распределением с теми же математическим ожиданием и дис­персией, определяемыми по формулам (5.28) и (5.29). Это аппроксимирующее рас­пределение дает приемлемые результаты, если nр и n(1-р) не ме­нее 5.

Распределение Пуассона является предельным случаем би­номиального распределения при р → 0, n → ∞.

То есть распределение Пуассона с параметром λ = np можно применять вместо биномиального, когда число опытов n достаточно велико, а вероятность р - достаточно ма­ла, т.е. в каждом отдельном опыте интересующее событие про­исходит крайне редко. Отсюда происходит применяющееся ино­гда для закона Пуассона название «закон редких явлений».

Гипергеометрическое распределение. Представим, что проверяется партия N изделий готовой продукции, содер­жащая М годных и N - М негодных изделий. Случайным обра­зом выбирают n изделий. Число годных изделий k, среди вы­бранных, описывается гипергеометрическим распределением. Математическое ожидание и дисперсия гипергеометрического распределения определяются соответственно выражениями (5.30) и (5.31).

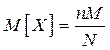(5.30)

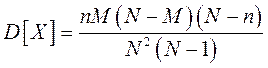(5.31)