Сравнение двух средних

Для сравнения между собой средних арифметических значений (средних) двух нормально распределенных выборок с однородными дисперсиями можно использовать распределение Стьюдента. Сравнение средних – это довольно часто возникающая необходимость при арбитраже результатов измерений (например, при спорах о показателях продукции между производителем и потребителем), для подтверждения достоверности выводов об изменении свойств объекта.

Для статистической проверки равенства двух средних (например, 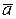и 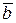из выборок a_i и b_i раздела 6.2) рассчитывают параметр t* по следующим формулам:

; .

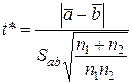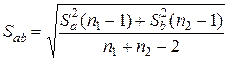Затем по распределению Стьюдента в зависимости от значений t* и степени свободы f* = n₁ + n₂ - 2 рассчитывают доверительную вероятность (Р) вывода о равенстве средних, либо для заданной вероятности, например из табл. 5.2, определяют значение критерия Стьюдента (t_Т). При использовании табличной формы распределения Стьюдента в качестве f используют степень свободы f *.

Если рассчитанное значение t* превосходит определенное t_Т (t* > t_Т), то с доверительной вероятностью можно считать средние различными. В противном случае (t* ≤ t_Т) для заданной доверительной вероятности можно предположить, что средние равны.

Пример [6]. Два аналитика (А и В), проводя анализ сплава на содержание бериллия одинаковым методом, получили следующие результаты.

Аналитики	Статистические параметры измерений
Число параллельных анализов, n	Средний результат, 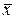, %	Выборочное абсолютное стандартное отклонение единичных значений, Sх, %
А	4	7,44	0,11
В	5	7,32	0,13

Есть ли расхождение средних результатов у двух аналитиков для доверительной вероятности Р=0,95?

Для ответа на этот вопрос выполним следующие процедуры. Из-за небольшого объема выборок n_a и n_b не будем определять закон их распределения, а сделаем допущение, что они подчиняются нормальному закону распределения.

Для проверки однородности дисперсий в этих выборках определим следующие параметры:

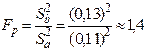; F_{Т(Р=0,95; f1=4;f2=3)} = 9,1.

Так как F_Р < F_Т (1,4 < 9,1), то следует считать сравниваемые дисперсии однородными и поэтому можно рассчитать значение выборочного средневзвешенного абсолютного стандартного отклонения S_ab:

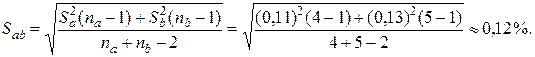
Вычислим параметр t*:

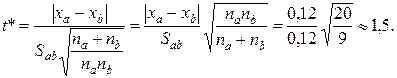
Из данных табл. 5.2 выбираем табличное значение квантиля распределения Стьюдента (t_Т) для f_ab = n_a +n_b -2 = 7 и заданной вероятности Р = 0,95 (β=0,05). Этот квантиль имеет значение t_Т = 2,37. Так как t* < t_Т (1,5 < 2,37), то средние результаты анализа сплава, полученные двумя аналитиками,следует считать одинаковыми.

6.5. Проверка нуль-гипотезы для рассчитанного
выборочного коэффициента парной линейной
корреляции

Для рассчитанного значения выборочного коэффициента парной линейной корреляции r_yx (коэффициента корреляции Пирсона) необходимо проводить статистическую проверку на равенство его нулю (проверка нуль-гипотезы).

При такой проверке можно использовать распределение Стьюдента [3]. В этом случае первоначально рассчитывают параметр t по следующей формуле:

,

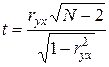где r_yx - выборочный коэффициент парной линейной корреляции;

N – общее число пар взаимосвязанных значений y и x (число точек на поле корреляции с соответствующими координатами y и x).

Затем по распределению Стьюдента в зависимости от значений t и степени свободы f = N - 2 рассчитывают доверительную вероятность (Р) вывода о равенстве нулю рассчитанного значения выборочного коэффициента парной линейной корреляции r_yx либо для заданной вероятности, например из табл. 5.2, определяют значение критерия Стьюдента (t_Т). Если рассчитанное значение t превосходит определенное t_Т (t > t_Т), то с доверительной вероятностью можно считать отличным от нуля значения выборочного коэффициента парной линейной корреляции r_yx. В противном случае (t ≤ t_Т) для заданной доверительной вероятности можно предположить, что значения выборочного коэффициента парной линейной корреляции r_yx равно нулю.

Пример [3]. По шести точкам на поле корреляции (N =6) был рассчитан выборочный парный коэффициент линейной корреляции r_yx = 0,800.

Визуальный анализ поля корреляции предполагает наличие положительной тесной линейной корреляционной связи между величинами y и x.

Для подтверждения или опровержения этого предварительного вывода выполним проверку рассчитанного значения r_yx на равенство его нулю (проверка нуль-гипотезы). Рассчитаем параметр t:

.

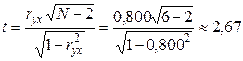Из данных табл. 5.2 выбираем табличное значение квантиля распределения Стьюдента (t_Т) для f = N -2 = 4 и вероятности Р = 0,95 (β=0,05). Этот квантиль имеет значение t_Т = 2,78. Так как t < t_Т (2,67 < 2,78), то с вероятностью Р=0,95 следует считать r_yx = 0, следовательно, можно предположить отсутствие линейной связи между величинами y и x.