| ЗМП | Динамические |
| Статические | Невыпуклое программирование |
| Выпуклое программирование | Нелинейноепрограммирование |
| Задачи Линейного Программирования (в т. ч. целочисленные, в т.ч. транспортные) |
Задачи выпуклого программирования - ЗМП, в которых и целевая функция и все ограничения – в ыпуклые функции.
ЗЛП – ЗМП, в которых и целевая функция и все ограничения – линейны относительно переменных задачи.
Задачи целочисленного (дискретного) программирования – задачи, переменные в которых могут только целые значения.
Транспортные задачи - ЗЛП в канонической форме, коэффициенты при переменных в ограничениях равны нулю или единице и каждая переменная входит в систему ограничений два раза.
Различают общую (см.(2)), каноническую и стандартную формы системы ограничений:
| Система ограничений линейной задачи вканонической формесостоит из однихравенств: | Система ограниченийЛЗ в стандартной формесостоит из неравенств одного направления: |
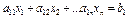
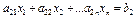 …….
…….
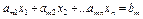
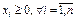
| 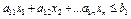
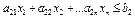 …….
…….
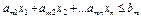
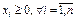
|
Приведение ЗЛП к каноническому виду: Если условия ограничения содержат неравенство, преобразовываем его в равенство, добавляя «слабые» переменные (со знаком «+» для «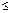 », и со знаком «-» для «
», и со знаком «-» для «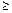 »). В целевую функцию слабые переменные входят с нулевыми коэффициентами.
»). В целевую функцию слабые переменные входят с нулевыми коэффициентами.
Приведение ЗЛП к стандартному виду: Изменяем знаки неравенств, умножая их на (-1). В равенства вводим дополнительные (слабые) переменные.
тема 2. Метод множителей Лагранжа решения ЗМП.
-это наиболее общий способ отыскания экстремума функции нескольких переменных, при наличии дополнительных уравнений, связывающих между собой эти переменные (нахождение условного экстремума).
Дано: Целевая функция задачи. 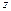 =
= 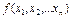
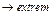
Система уравнений – m ограничений на переменные: 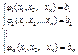
Решение: Составим функцию Лагранжа: 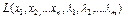 =
=
= 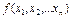 +
+ 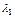 [
[ 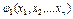 -
- 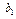 ] +
] + 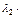 [
[ 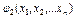 -
- 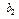 ] + …+
] + …+ 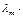 [
[ 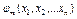 -
- 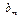 ],
],
где 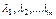 - новые неизвестные задачи, множители Лагранжа.
- новые неизвестные задачи, множители Лагранжа.
Найдём безусловный экстремум полученной функции. Воспользуемся необходимым условием существования экстремума для функции двух переменных:
Если функция 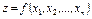 достигает экстремума в точке М0
достигает экстремума в точке М0 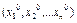 , то все её первые частные производные в этой точке равны нулю или не существуют.
, то все её первые частные производные в этой точке равны нулю или не существуют.
Найдём все частные производные этой функции, приравняем их к нулю и составим систему уравнений:
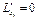 ,
, 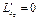 , …,
, …, 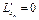 ,
, 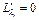 ,
, 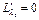 , …,
, …, 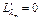
Каждое решение данной системы – критическая точка, принадлежащая ОДР задачи.
Если точек несколько, выбираем из них наибольшее и наименьшее значение.
Если точка единственная, воспользуемся достаточным условием существования экстремума:
Составим матрицу Гессе из вторых частных производных функции Лагранжа.
Если 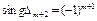 и далее знаки главных миноров матрицы чередуются, то критическая точка- точка максимума. Если
и далее знаки главных миноров матрицы чередуются, то критическая точка- точка максимума. Если 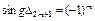 и далее знаки чередуются, то критическая точка- точка минимума.
и далее знаки чередуются, то критическая точка- точка минимума.
Экономический смысл множителей Лагранжа. Множители Лагранжа 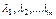 указывают, как изменится оптимальное значение целевой функции при изменении соответствующих им параметров задачи
указывают, как изменится оптимальное значение целевой функции при изменении соответствующих им параметров задачи 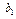 ,
, 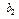 , …,
, …, 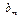 на единицу. То есть k-тый множитель Лагранжа определяет ценность k-того ресурса.
на единицу. То есть k-тый множитель Лагранжа определяет ценность k-того ресурса.
 2015-03-22
2015-03-22 573
573








