Если частные производные 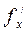 и
и 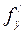 функции
функции 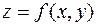 сами являются дифференцируемыми функциями, то можно найти также и их частные производные, которые называются частными производными второго порядка, то есть
сами являются дифференцируемыми функциями, то можно найти также и их частные производные, которые называются частными производными второго порядка, то есть
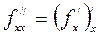 ,
, 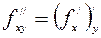 ,
, 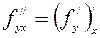 ,
, 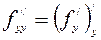 .
.
Аналогично определяются частные производные 3-го, 4-го и т.д. порядков. Частная производная второго и более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Имеет место следующая теорема.
Теорема. Если частные производные второго порядка функции  непрерывны в точке
непрерывны в точке 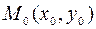 , то в этой точке смешанные частные производные равны, то есть
, то в этой точке смешанные частные производные равны, то есть  .
.
Пример. Найти частные производные второго порядка функции 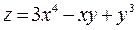 .
.
Решение. Так как 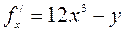 ,
, 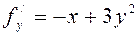 , то
, то
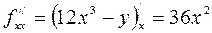 ,
, 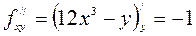 ,
,
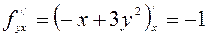 ,
, 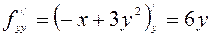 .
.
Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной переменной.
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Точка
. Точка  называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции  , если существует такая
, если существует такая 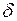 - окрестность точки
- окрестность точки  , что во всех ее точках
, что во всех ее точках 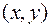 , отличных от
, отличных от  , выполнятся неравенство
, выполнятся неравенство 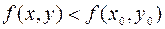 (
(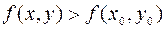 ).
).
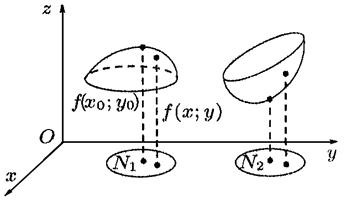 Рис. 9 Рис. 9 |
На рисунке 9: 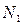 – точка максимума, а
– точка максимума, а 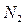 – точка минимума функции
– точка минимума функции  . Максимум и минимум функции называются ее экстремумами.
. Максимум и минимум функции называются ее экстремумами.
Теорема (необходимые условия экстремума). Если в точке  дифференцируемая функция
дифференцируемая функция  имеет экстремум, то ее частные производные в этой точке равны нулю:
имеет экстремум, то ее частные производные в этой точке равны нулю: 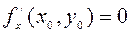 ,
, 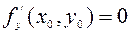 .
.
Геометрически равенства  и
и 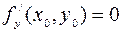 означают, что в точке экстремума функции касательная плоскость к поверхности, изображающей функцию
означают, что в точке экстремума функции касательная плоскость к поверхности, изображающей функцию  , параллельна плоскости
, параллельна плоскости 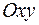 , так как уравнение касательной плоскости есть
, так как уравнение касательной плоскости есть 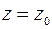 .
.
Замечание. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например, функция 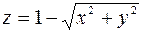 имеет максимум в точке
имеет максимум в точке 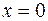 ,
, 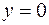 (см. рис. 10), но не имеет в этой точке частных производных.
(см. рис. 10), но не имеет в этой точке частных производных.
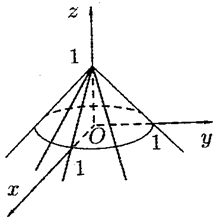 Рис. 10 Рис. 10 |
Точки, в которой частные производные первого порядка функции  равны нулю, то есть
равны нулю, то есть 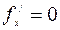 и
и 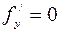 , и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.
, и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.
В критических точках функция  может иметь экстремум, а может и не иметь. Условия
может иметь экстремум, а может и не иметь. Условия 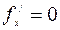 и
и 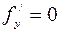 являются необходимыми, но не достаточными условиями существования экстремума. Так, например, для функции
являются необходимыми, но не достаточными условиями существования экстремума. Так, например, для функции 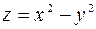 точка (0,0) является критической (в ней
точка (0,0) является критической (в ней 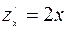 и
и 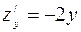 обращаются в ноль), однако, очевидно, никакого экстремума в этой точке нет (см. рис. 11).
обращаются в ноль), однако, очевидно, никакого экстремума в этой точке нет (см. рис. 11).
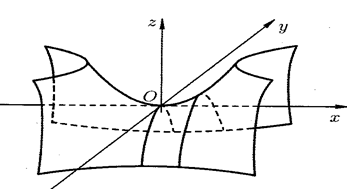 Рис. 11 Рис. 11 |
Теорема (достаточные условия экстремума). Пусть в некоторой окрестности стационарной точки  функция
функция  имеет непрерывные частные производные до второго порядка включительно причем
имеет непрерывные частные производные до второго порядка включительно причем 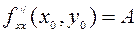 ,
, 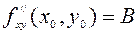 ,
, 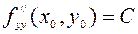 .
.
Обозначим
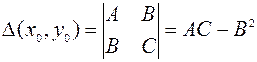 .
.
Тогда:
1) если 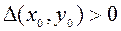 , то функция
, то функция  в точке
в точке  имеет экстремум: максимум, если
имеет экстремум: максимум, если 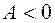 , и минимум, если
, и минимум, если 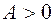 ;
;
2) если 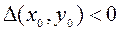 , то функция
, то функция  в точке
в точке  экстремума не имеет;
экстремума не имеет;
3) если 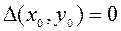 , то экстремум в точке
, то экстремум в точке  может быть, может не быть. Необходимы дополнительные исследования.
может быть, может не быть. Необходимы дополнительные исследования.
Пример. Найти точки экстремума функции 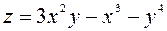 .
.
Решение. 1) Найдем частные производные первого порядка: 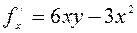 ,
, 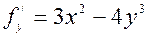 . Точки, в которых частные производные не определены отсутствуют.
. Точки, в которых частные производные не определены отсутствуют.
2) Найдем стационарные точки, решая систему уравнений:
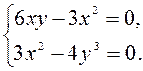
Отсюда получаем две точки: 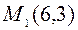 и
и 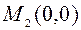 .
.
3) Находим частные производные второго порядка данной функции: 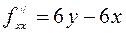 ,
, 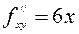 ,
, 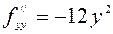 .
.
4) В точке 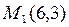 имеем:
имеем: 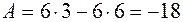 ,
, 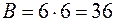 ,
, 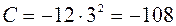 , отсюда
, отсюда 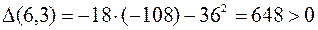 , то есть
, то есть 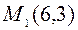 – точка экстремума. Так как
– точка экстремума. Так как 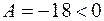 , то
, то 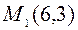 – точка максимума.
– точка максимума.
В точке 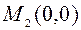 :
: 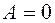 ,
, 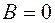 ,
, 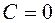 , отсюда
, отсюда 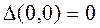 . Проведем дополнительное исследование. Значение функции
. Проведем дополнительное исследование. Значение функции 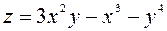 в точке
в точке 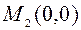 равно нулю. Рассмотрим точки из окрестности точки
равно нулю. Рассмотрим точки из окрестности точки 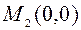 такие, что
такие, что 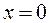 , тогда
, тогда 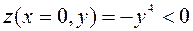 , а теперь рассмотрим точки из той же окрестности, но с условием
, а теперь рассмотрим точки из той же окрестности, но с условием 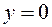 ,
, 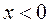 :
: 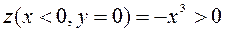 . Таким образом, в любой окрестности точки
. Таким образом, в любой окрестности точки 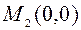 функция
функция 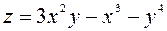 принимает как отрицательные, так и положительные значения. Следовательно, в точке
принимает как отрицательные, так и положительные значения. Следовательно, в точке 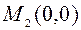 функция экстремума не имеет.
функция экстремума не имеет.
 2015-03-22
2015-03-22 3210
3210
