Линейные однородные дифференциальные уравнения

Используя свойства линейного дифференциального оператора, сформу­ли­руем свойство решений линейного дифференциального уравнения (4), которое дает ключ к пониманию структуры (устройства) общего решения.

Если h (x) и g (x) − решения линейного однородного уравнения (4), то для любых констант С ₁ и С ₂ функция j (х) = С ₁ h (x) + С ₂ g (x) − решение урав­нения (4).

Известно, что общее решение уравнения n -го порядка содержит n произ­вольных констант. В связи с этим возникают следующие вопросы. Можно ли найти такие n решений j₁(х), j₂(х) ,..., j _n (х), что функция

j (х) = 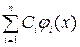, (5)

где Сi (i = 1, 2 ,..., n) − константы, будет общим решением линейного однород­ного уравнения (4)? Какими свойствами должны обладать функции j _i (х), что­бы составленная из них по формуле (5) функция являлась общим решением?

На основании свойства решений линейных однородных диффе­ренциальных уравнений можно сделать вывод, что множество всех решений данного уравнения образует линейное пространство. Известно, что в любом линейном пространстве каждый элемент является линейной комбинацией базиса.

Введем понятия линейной зависимой и линейной независимой системы функций.

Определение 2. Система функций y ₁(х), y ₂(х), ..., y_m (х) называется линей­но зависимой на интервале (a, b), если на этом интервале выполняется тож­дест­во:

α₁ y ₁(х) + α₂ y ₂(х) +...+ α _m y_m (х) ≡ 0, (6)

в котором, по крайней мере, один из коэффициентов α _i (i = 1, 2,..., m) отличен от нуля (α₁² + α₂² +... + α _m ² ≠ 0).

Определение 3. Система функций y ₁(х), y ₂(х), ..., y_m (х) называется линейно независимой на интервале (a, b), если на этом интервале тождество (6) выпол­няется только в том случае, когда все коэффициенты α _i (i = 1, 2,..., m) равны нулю (α₁² + α₂² +... + α _m ² = 0).

Пример 2. Исследовать на линейную зависимость системы функций:

а) у ₁(х) = х, у ₂(х) = 3 х;

б) у ₁(х) = sinх, у ₂(х) = cosх.

Решение. В случае (а) тождество α₁ y ₁(х) + α₂ y ₂(х) ≡ 0 выполняется при α₁ = −3 и α₂ = 1 для всех х, т. е. по определению 2 эта система функций линей­но зависима на всей числовой прямой.

В случае (б) предположим, что α₁ sinх + α₂ cosх ≡ 0 и один из коэффици­ентов, допустим α₁, отличен от нуля. Тогда

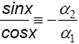
показывает, что это невозможно, так как выражение слева зависит от х, а спра­ва − константа. Таким образом, функции sinx и сosx являются линейно незави­си­мой системой на (−∞, ∞).

Анализируя решение примера 2, можно сформулировать утверждение общего характера: система, состоящая из двух функций, линейно зависима тогда и только тогда, когда их отношение является константой.

Для того чтобы сформулировать условия линейной зависимости систе­мы функций, нам потребуется понятие определителя Вронского (вронскиана).

Определение 4. Определителем Вронского системы функций y ₁(х), y ₂(х) ,..., y_m (х) называется функциональный определитель порядка m:

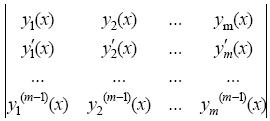= W [ y ₁, y ₂, ..., y_m ]. (7)

Пример 3. Найти определитель Вронского системы функций:

а) у ₁(х) = х, у ₂(х) = 3 х;

б) у ₁(х) = sinх, у ₂(х) = cosх.

Решение. В случае (а)

W [ x, 3 x ] = .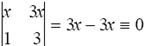

Для системы функций у ₁(х) = sinх, у ₂(х) = cosх имеем

W [ sinx, cosx ] =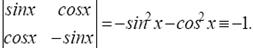

Теорема 2 (необходимое условие линейной зависимости) Если система функций y ₁ (х), y ₂ (х),..., y_m (х) линейно зависима на интервале (а, b), то ее определитель Вронского W [ y ₁, y ₂ ,..., y_m ] ≡ 0 на (a, b).

В примере 2 (а) мы установили линейную зависимость системы функций, а в примере 3 (а) показали, что ее определитель Вронского равен нулю. Данное условие является необходимым, но недостаточным. Сформулируем необходи­мое и достаточное условие линейной зависимости не для произвольной систе­мы функций, а для решений линейного однородного дифференциального уравнения.

Теорема 3. Функции y ₁ (х), y ₂ (х),..., y_m (х) − решения линейного дифференциального уравнения (4), все коэффициенты которого непре­рывны на интервале (а, b), образуют линейно независимую систему тогда и только тогда, когда ее определитель Вронского W [ y ₁, y ₂ ,..., y_m ] ≠ 0 ни в одной точке интервала (a, b).

Пример 4. Очевидно, что функции у ₁(х) = sinх, у ₂(х) = cosх являются решениями уравнения у ′′(х) + у (х) = 0. По теореме 3 мы можем утверждать, что они линейно независимы на всей числовой оси, так как W [ sinx, cosx ] ≡ −1 (см. пример 3).

Для установления линейной независимости решений линейного одно­род­ного дифференциального уравнения нужно по теореме 3 проверить, что определитель Вронского ни в одной точке интервала не равен нулю. В этом заключается неудобство данного критерия. Однако его можно упростить, если воспользоваться формулой Остроградского − Лиувилля:

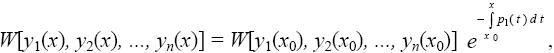(8)

где y ₁(х), y ₂(х), ..., у_n (x) − решения линейного однородного дифференциального уравнения (4), в котором все коэффициенты непрерывны на интервале (а, b), х ₀∈ (а, b) и р ₁(t) − коэффициент перед производной (n − 1)-го порядка в (4).

Действительно, равенство (8) означает: из того, что определитель Вронс­кого не обращается в нуль в некоторой точке х ₀∈ (а, b) следует, что он не равен нулю ни в какой другой точке этого интервала, так как функция е^х ≠ 0 при любом х. Таким образом, получаем

Следствие. Совокупность n решений линейного однородного дифферен­циального уравнения порядка n с непрерывными на (а, b) коэффициентами линейно независима тогда и только тогда, когда определитель Вронского отличен от нуля хотя бы в одной точке этого интервала.

Определение 5. Совокупность n решений линейного однородного диф­фе­ренциального уравнения n -го порядка, которая определена и линейно независима на интервале (a, b), называется фундаментальной системой решений (ФСР) этого уравнения.

Теорема 4. Если коэффициенты линейного однородного дифферен­циального уравнения порядка n непрерывны на интервале (а, b), то для него на этом интервале существует фундаментальная система решений:

y ₁(х), y ₂(х) ,..., y_n (х).

Следующая теорема дает ответ на один из основных вопросов в теории линейных дифференциальных уравнений.

Теорема 5. Если y ₁(х), y ₂(х) ,..., y_n (х) − фундаментальная система решений линейного однородного дифференциального уравнения порядка n, то его общее решение определяется формулой

y (x) = С ₁ y ₁(х) + С ₂ y ₂(х) +... + С_ny_n (х), (9)

где С_i (i = 1, 2,..., n) − произвольные константы.

Таким образом, теорема 5 фактически утверждает, что пространство ре­ше­ний данного линейного однородного уравнения n -го порядка имеет базис − ФСР, который состоит из n решений.

Пример 5. Показать, что функции у ₁(х) = sinх, у ₂(х) = cosх образуют фун­даментальную систему решений уравнения у ′′(х) + у (х) = 0. Записать общее решение уравнения.

Решение. Очевидно, что функции у ₁(х) = sinх, у ₂(х) = cosх удовлетворяют данному уравнению. По теореме 3 они линейно независимы на всей числовой оси, так как W [ sinx, cosx ] ≡ −1 (см. пример 3). Таким образом, они являются фундаментальной системой решений. Общим решением является функция у (х) = С ₁ sinx + C ₂ cosx (cм. теорему 5).