До сих пор мы рассматривали определенный интеграл с постоянными пределами интегрирования a и b. Пусть функция f (x) интегрируема на отрезке [ a, b ]. Если x ∈ [ a, b ], то функция f (x) также интегрируема на любом отрезке [ a, x ]. Если изменять верхний предел, не выходя из отрезка [ a, b ], то величина интеграла будет изменяться, т. е. интеграл
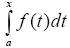
с постоянным нижним пределом a и переменным верхним пределом x есть функция верхнего предела. Обозначим эту функцию Ф (x):

Замечание. Для удобства переменная интегрирования здесь обозначена буквой t, так как буквой x обозначен верхний предел интегрирования. Интеграл (8) называется интегралом с переменным верхним пределом.
Сформулируем основную теорему дифференциального и интегрального исчисления, устанавливающую связь между производной и интегралом.
Теорема 3. Производная интеграла от непрерывной функции по переменному верхнему пределу существует и равна значению подынтегральной функции в точке, равной верхнему пределу, т. е.
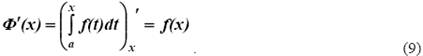
Эта теорема утверждает, что любая непрерывная функция на отрезке [ a, b ] имеет на нем первообразную, причем этой первообразной является функция Ф (x), а так как всякая другая первообразная функции f (x) может отличаться от данной Ф (x) лишь на постоянную, то устанавливается связь между неопределенным и определенным интегралом
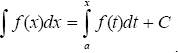
Теорема 4. Если функция f(x) непрерывна на отрезке [ a, b ], то
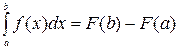 , (10)
, (10)
где F(x) − некоторая первообразная функции f(x).
Формула (10) называется формулой Ньютона-Лейбница. Формулу Ньютона-Лейбница можно переписать как
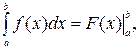 где
где 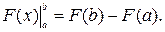
Вывод. Определенный интеграл 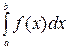 от непрерывной функции f (x) равен разности значений любой первообразной для верхнего и нижнего пределов интегрирования.
от непрерывной функции f (x) равен разности значений любой первообразной для верхнего и нижнего пределов интегрирования.
Формула Ньютона-Лейбница открывает широкие возможности для вычисления определенных интегралов, так как задача сводится к задаче вычисления неопределенных интегралов.
Если считать переменным нижний предел интегрирования, то пользуясь формулой Ньютона-Лейбница, получим

Теорема 5. Если f(x) − непрерывная, φ(x), ψ(x) − дифференцируемые функции, то производная от интеграла 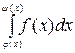 по переменной x
по переменной x
6p> 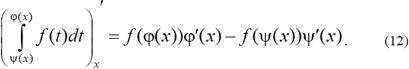
Пример. Найти производную по x от интеграла 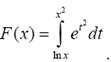
Решение. Здесь 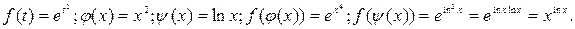
φ? (x) = 2 x, 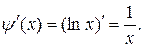
Пользуясь формулой (12), получим
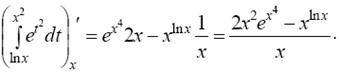
 2015-03-22
2015-03-22 21334
21334
