§1. Поток вектора через замкнутую поверхность. Теорема Гаусса-Остроградского.
Теорема 4.1: Если в некоторой области G пространства координаты вектора
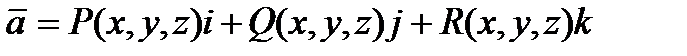
непрерывны и имеют непрерывные частные производные 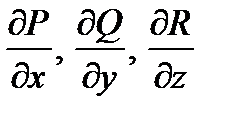 , то поток вектора
, то поток вектора 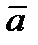 через любую замкнутую кусочно гладкую поверхность Σ, расположенную в области G, равен тройному интегралу от
через любую замкнутую кусочно гладкую поверхность Σ, расположенную в области G, равен тройному интегралу от 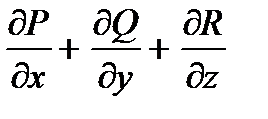 по области V, ограниченной поверхностью Σ:
по области V, ограниченной поверхностью Σ:
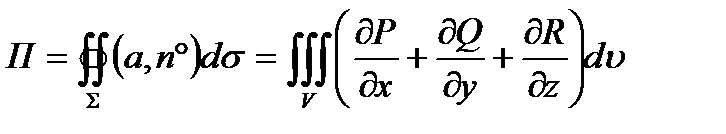 (4.1)
(4.1)
(формула Гаусса-Остроградского).Нормаль  к поверхности Σ берётся внешняя.
к поверхности Σ берётся внешняя.
Пример 4.1. Вычислить поток вектора
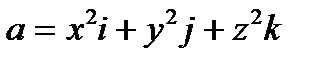
через замкнутую поверхность
x2 + y2 + z2 = R2, z = 0 (z>0).
Решение. По формуле 4.1
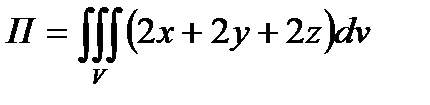 (4.2)
(4.2)
Интеграл (4.2) удобно вычислять в сферических координатах 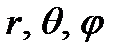 . Имеем
. Имеем
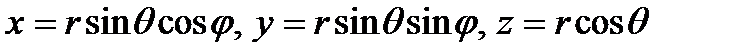
и элемент объёма
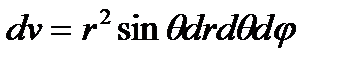
так что
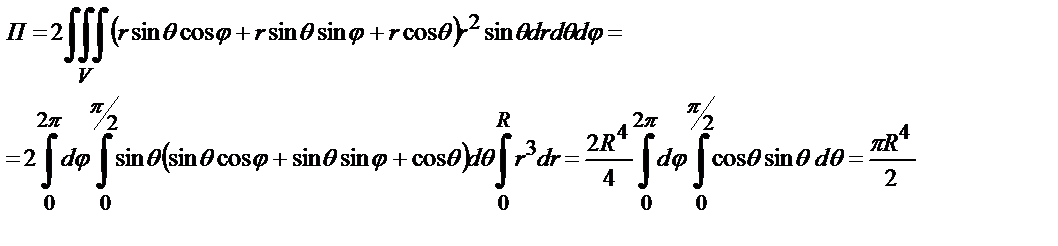
Пример 4.2. Вычислить поток вектора 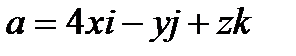 через поверхность тора.
через поверхность тора.
Решение. Воспользовавшись теоремой Гаусса-Остроградского, получим, что искомый поток П равен
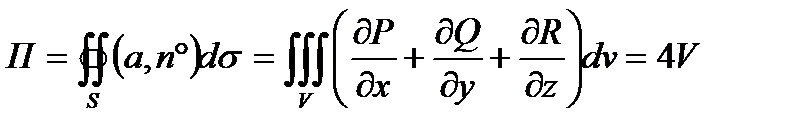
где V – объём тора. Чтобы вычислить объём V, воспользуемся теоремой Гюльдена об объёме тела вращения, в силу которой этот объём равен произведению площади вращающейся фигуры на путь, описываемый центром масс этой фигуры при вращении.
|
|
|
Пусть R1 и R2 - внутренний и внешний радиусы тора (рис.4.1). Площадь S круга, который при вращении образует тор, равна
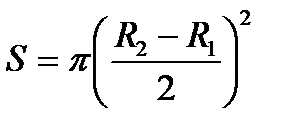
Длина пути, описываемого центром масс – центром этого круга, - есть длина l окружности радиуса 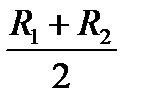 , то есть.
, то есть.
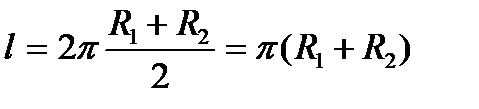
Таким образом, объём V тора равен
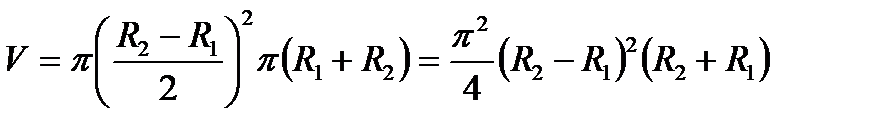
Искомый поток
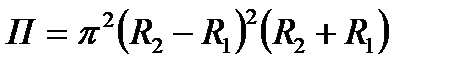
| Z R1 X R2 Рисунок 4.1 |
| Z n° σ1 k j Y i σ2 X n°=-k Рисунок 4.2 |
Пример 4.3. Используя теорему Гаусса – Остроградского, вычислить поток векторного поля
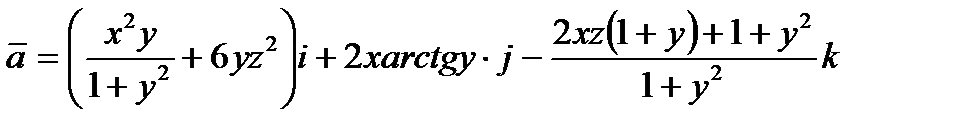
через внешнюю сторону части поверхности z = 1 - x2 - y2, расположенной над плоскостью XOY.
Решение. Для того чтобы можно было применить теорему Гаусса – Остроградского, замкнем снизу данную поверхность куском плоскости XOY, который ограничен окружностью
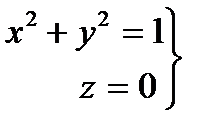
Пусть v – объём полученного тела, ограниченного замкнутой кусочно гладкой поверхностью σ, состоящей из части σ1 параболоида вращения z = 1 - x2 - y2 и части σ2 плоскости z = 0. (рис. 4.2).
Поток данного вектора через поверхность σ по теореме Гаусса – Остроградского равен
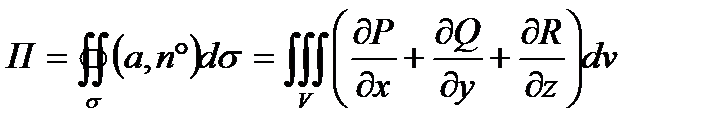
Находим сумму
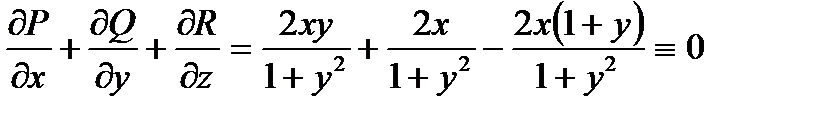
Следовательно, поток
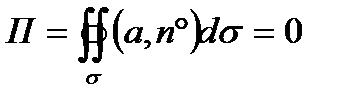
В силу аддитивности потока будем иметь
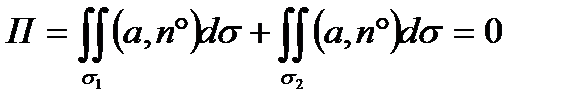
Отсюда искомый поток
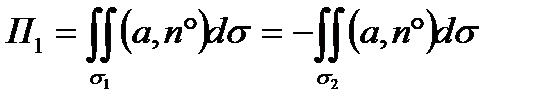
Поток П2 вектора а через круг 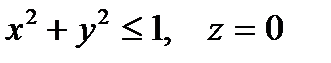 равен
равен
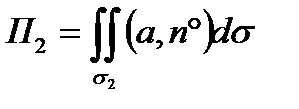
Так как на плоскости z=0 имеем
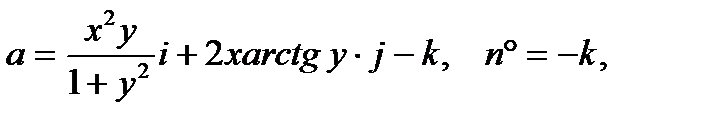
и следовательно (a,n°) = 1, то поток П2 через круг σ2 будет равен площади круга σ2
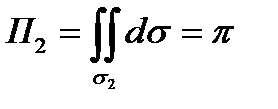
Искомый поток П1 = -П2 = -π
§2. Дивергенция векторного поля.
Понятие потока вектора через замкнутую поверхность приводит к понятию о дивергенции или расходимости поля. Это понятие даёт некоторую количественную характеристику поля в каждой его точке.
Пусть М – изучаемая точка поля. Окружим её поверхностью Σ произвольной формы, например, сферой достаточно малого радиуса. Область, ограниченная поверхностью Σ, пусть будет (V), а её объём V. Рассмотрим отношение
|
|
|
 (4.3)
(4.3)
Определение 4.1. Если отношение (4.3) имеет конечный предел, когда область (V) стягивается к точке М, то этот предел называется дивергенцией векторного поля (дивергенцией вектора а) в точке М и обозначают символом div a (M). Так что
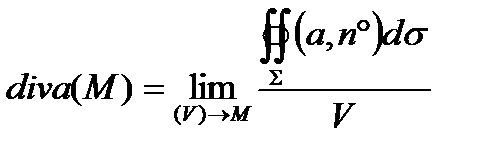 (4.4)
(4.4)
Формула (4.4) даёт инвариантное определение дивергенции. Это определение означает, что дивергенция поля а в точке М есть объёмная плотность потока вектора а в этой точке.
Точки М векторного поля а(М), в которых div a>0, называются источниками, а точки, в которых div a<0 называются стоками векторного поля.
Дивергенция векторного поля есть скалярная функция точек поля.
Если координаты вектора
a(M) = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k
имеют непрерывные частные производные 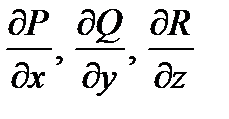 в окрестности точки М(x, y, z), то, пользуясь инвариантным определением дивергенции, из теоремы Гаусса – Остроградского получаем, что
в окрестности точки М(x, y, z), то, пользуясь инвариантным определением дивергенции, из теоремы Гаусса – Остроградского получаем, что
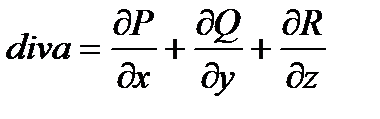 (4.5)
(4.5)
Все величины в формуле (4.5) рассматриваются в одной и той же точке М(x, y, z).
Используя формулу (4.5) для дивергенции, можно теорему Гаусса – Остроградского (см. §1) записать в векторной форме
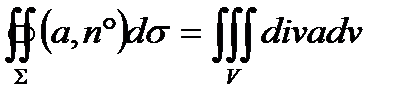 (4.6)
(4.6)
Пример 4.4. Пользуясь инвариантным определением, вычислить дивергенцию вектора a = xi в точке О(0, 0, 0), выбрав в качестве поверхностей σ окружающих точку О, сферы σε радиуса ε с центром в этой точке.
Решение. По определению дивергенции в данной точке имеем
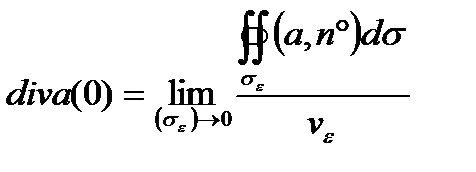
где v ε – объём шара, ограниченного сферой σε, или
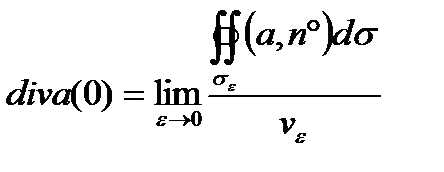
Но так как объём шара равен 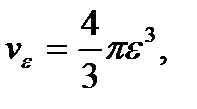 то
то
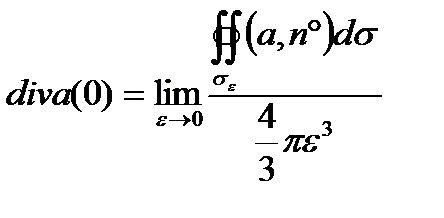
Вычислим поток 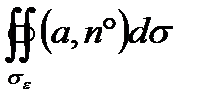 данного вектора через сферу σε. Орт нормали n ° к сфере σε направлен по радиусу сферы, поэтому можно положить:
данного вектора через сферу σε. Орт нормали n ° к сфере σε направлен по радиусу сферы, поэтому можно положить:
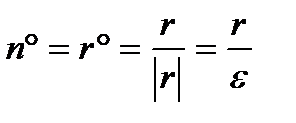
где r ° - орт радиуса-вектора r = xi + yj + zk, или
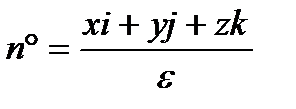
Искомый поток будет равен
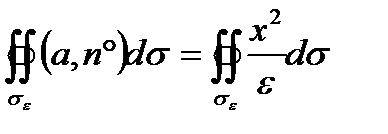
Переходя к координатам на сфере σε
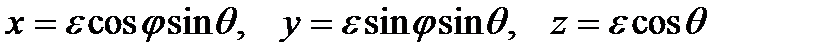
получим
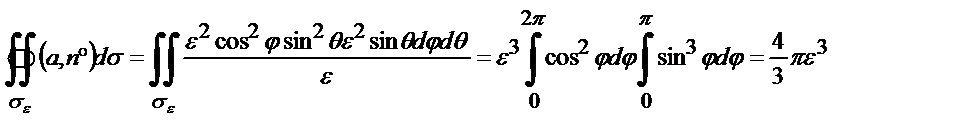
Следовательно
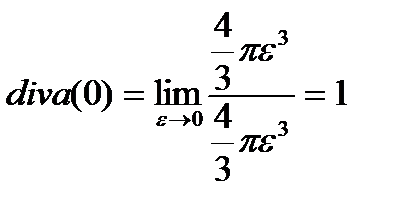
Пример 4.5. Вычислить div r.
Решение. Имеем 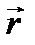 = xi + yj + zk, так что P = x, Q = y, R = z и, значит, по формуле (4.5)
= xi + yj + zk, так что P = x, Q = y, R = z и, значит, по формуле (4.5)
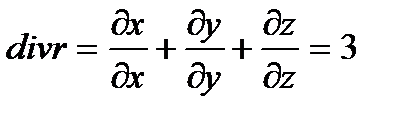
Пример 4.6. Вычислить div(u,a), где u(M) – скалярная функция, а(М) = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k – векторная функция.
Решение. Используя формулу (4.5), находим
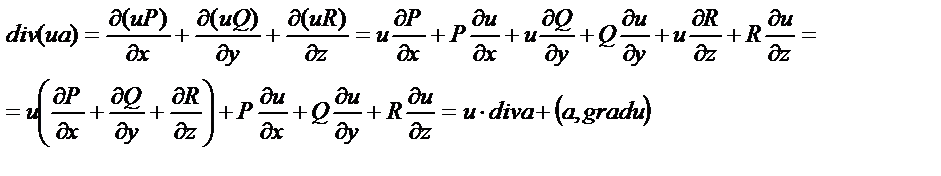
Итак,
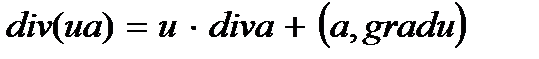 (4.7)
(4.7)
Пример 4.7. Найти дивергенцию вектора

где 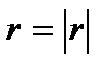 - расстояние от начала координат до переменной точки M(x, y, z).
- расстояние от начала координат до переменной точки M(x, y, z).
Решение. Используя формулу (4.7), получим
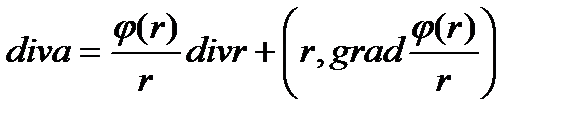 .
.
Далее, 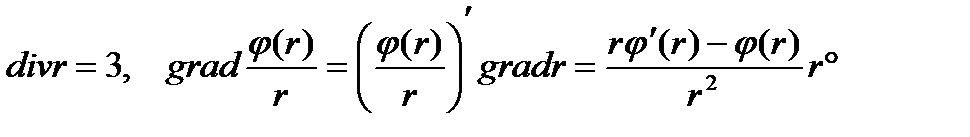
поэтому
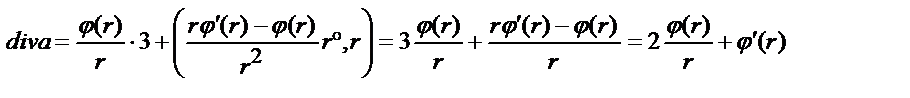
 2015-03-07
2015-03-07 20470
20470
