При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Одним из наиболее эффективных методов является метод золотого сечения. Он состоит в построении последовательности отрезков 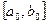 ,
, 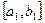 , …, стягивающихся к точке минимума функции. На каждом шаге, за исключением первого, вычисление значения функции производится один раз в точке, называемой золотым сечением. Золотое сечение интервала выбирается так, чтобы отношение длины большего отрезка
, …, стягивающихся к точке минимума функции. На каждом шаге, за исключением первого, вычисление значения функции производится один раз в точке, называемой золотым сечением. Золотое сечение интервала выбирается так, чтобы отношение длины большего отрезка 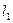 к длине всего интервала
к длине всего интервала 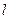 равнялось отношению длины меньшего отрезка
равнялось отношению длины меньшего отрезка 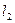 к длине большего отрезка
к длине большего отрезка 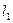 :
:
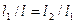 ,
,
Из этого соотношения можно найти точку деления:
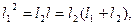
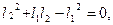
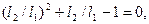
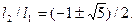
Так как нас интересует только положительное решение, то
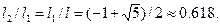
Отсюда
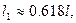
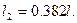
Поскольку заранее неизвестно в какой последовательности (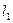 и
и 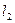 или
или 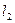 и
и 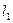 ) делить интервал неопределенности, то рассматривают внутренние точки, соответ-ствующие двум этим способам деления.
) делить интервал неопределенности, то рассматривают внутренние точки, соответ-ствующие двум этим способам деления.
Точки 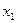 и
и 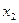 выбирают с учетом полученных значений частей отрезка. В данном случае:
выбирают с учетом полученных значений частей отрезка. В данном случае:
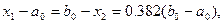
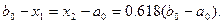
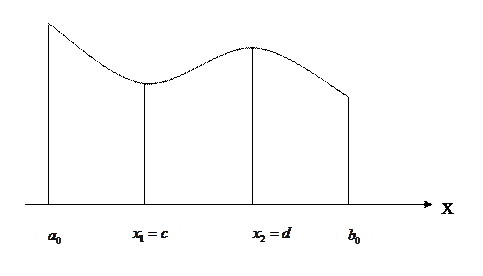
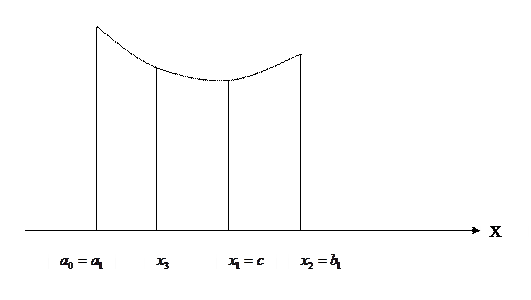
После первого шага оптимизации получается новый интервал неопределенности 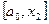 . Точка
. Точка 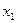 делит этот отрезок в требуемом отношении, т. е.
делит этот отрезок в требуемом отношении, т. е.
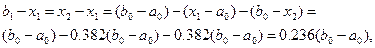
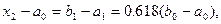
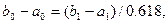
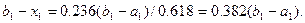
Вторая точка 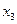 выбирается на таком же расстоянии от левой границы отрезка, т.е.
выбирается на таком же расстоянии от левой границы отрезка, т.е.
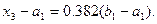
И снова интервал неопределенности уменьшается до величины
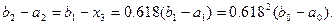
Используя полученные соотношения, можно записать координаты точек деления 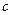 и
и 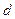 на отрезке
на отрезке 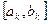 на
на 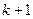 шаге:
шаге:
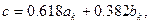
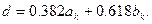
При этом длина интервала неопределенности равна:
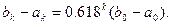
Процесс оптимизации заканчивается при выполнении условия
- Метод Фибоначчи
Метод Фибоначчи – разновидность одномерного поиска экстремума функции путем последовательного сужения интервала неопределенности. Единственное ограничение, налагаемое на исследуемую функцию f (x) – требование строгой унимодальности на заданном интервале.
При последовательном сужении значения f (x) вычисляются (или замеряются) в заранее ограниченном числе пробных точек. В результате получается последовательность сужающихся интервалов неопределенности, содержащих искомый экстремум:
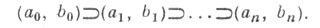
Чтобы сузить интервал неопределенности для произвольной строго унимодальной функции, нужно знать не менее двух ее пробных значений. В методе Фибоначчи внутри каждого текущего интервала неопределенности (ai, bi) подбираются ровно две пробные точки симметрично от середины интервала. Далее, от одной из пробных точек отбрасывается конец интервала с наихудшими значениями f (x). Получается (а i+1, bi+1), где в дополнение к оставшейся старой пробной точке симметрично строится новая. Отсюда для длин интервалов 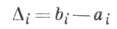 следует рекуррентное уравнение
следует рекуррентное уравнение
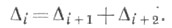
(Помимо прочего выше предполагалось, что выполнено условие перекрывания 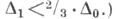
Решение уравнения при условии 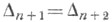 дает
дает
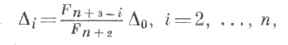
где 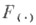 – числа Фибоначчи:
– числа Фибоначчи:
F0 = 0, F1 = 1, Fn = Fn – 1 + Fn –2.
Точка экстремума 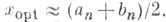
В простейшем варианте метода Фибоначчи (когда предполагается, что пробные точки и пробные значения f (x) определяются абсолютно точно), чтобы сузить исходный интервал неопределенности с 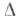 до
до 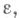 надо взять число пробных точек из неравенства
надо взять число пробных точек из неравенства

 2015-03-27
2015-03-27 515
515








